[支持向量机SVM] 西瓜书+个人理解 【2.KKT条件】

我们上一节得到了SVM的基本型：

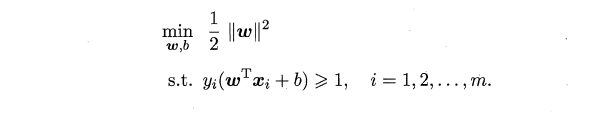
我们通过观察可以发现svm的基本型是一个有约束的优化问题。
有约束优化问题可分为两种：等式约束，不等式约束。如果我们可用g(x)=0表示等式约束，g(x)≤0来表示不等式约束。设原目标优化函数为f(x),我们分别来看一下这两种情况：

1. 等式约束，最优解x一定满足，g(x)=0,且原函数在最优解的梯度▽f(x*)向量必与g(x)=0在这点的的切线方向垂直。而一个函数的梯度向量必然与其等值线垂直,我们可以把g(x) = 0当做g(x)的一条等值线，所以g(x)在x这一点的梯度▽g(x)向量与▽f(x*)在同一条直线上，即▽g(x*) + λ▽f(x*) = 0（g(x) = 0）。
   通常对于等式约束下的优化问题我们使用拉格朗日乘子法，我们构造拉格朗日函数L(x,λ) = f(x) + λg(x)，然后分别对x,λ求偏导，另其等于0得到：①▽g(x*) + λ▽f(x*) = 0，②g(x) = 0。

2. 不等式约束，也就是g(x)≤0为约束条件，最优解满足g(x*)≤0。可分为两种情况：
   Ⅰ. 最优解在g(x)≤0区域的边缘上，也就是最优解x满足g(x)=0,此时与等式约束 相同。此时g(x)的梯度方向与f(x)的梯度方向相反，也就是式子▽g(x*) + λ▽f(x*) = 0中λ>0。
   Ⅱ. 最优解在g(x)≤0区域内部,那么不等式约束g(x)≤0并没有起到作用，那么对L(x,λ)的最优化与直接对f(x)的最优化没有差别，也就是λ=0。
   对于上述ⅠⅡ两种情况我们可以总结出三个式子:
   
   此三个条件我们称之为Karush-Kuhn-Tucker条件，简称KKT条件。