线性代数——行列式

最新推荐文章于 2023-11-02 10:01:58 发布

临危诡局

最新推荐文章于 2023-11-02 10:01:58 发布

阅读量2.7k

点赞数 4

文章标签：线性代数

本文链接：https://blog.csdn.net/lcq2468/article/details/124170888

版权

# 个人复习用，来源于2022张宇考研九讲

定义

行列式是由n个n维向量组成，其运算规则为n个向量为邻边的n为图形的有向体积。

若Diag(A)= 0，则说明V=0，即有向量组线性相关
若Diag(A) $\neq$ 0，则说明V $\neq$ 0，即向量线性无关

性质

行列互换，值不变（行列地位相等）
某行元素全为零，值为零
两行元素为倍数关系，值为零
单行可拆分成两个元素之和，其余行不变，变成两个行列式之和
任意两行互换，值相反
单行可提公因式
行列式某行k倍加到另一行，值不变

展开定理

余子式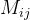 $M_{ij}$

剩余的行列式（去掉 $a_{ij}$ 所在行与列后的n-1阶）

代数余子式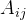 $A_{ij}$

$A_{ij}=(-1)^{i+j}M_{ij}$ ，反过来也是一样的关系

按某一行展开

$|A|=a_{i1}A_{i1}+a_{i2}A_{i2}+...+a_{in}A_{in}=\sum_{j=1}^{n}a_{ij}A_{ij}(i=1,2,...,n)$

具体数值型行列式计算

12+1

主对角线

左下或右上三角全为零，值为主对角线元素之积

副对角线

左上或右下三角全为0，值为 $(-1)^{\frac{n(n-1)}{2}}\prod_{i=1}^{n}a_{i,(1+n-i)}$

拉普拉斯展开式

A为m阶方阵，B为n阶方阵，则

$\begin{vmatrix} A & 0\\ 0 & B \end{vmatrix}=\begin{vmatrix} A & C\\ 0 & B \end{vmatrix}=\begin{vmatrix} A & 0\\ C & B \end{vmatrix}=|A||B|$

$\begin{vmatrix} 0 & A\\ B & 0 \end{vmatrix}=\begin{vmatrix} C & A\\ B & 0 \end{vmatrix}=\begin{vmatrix} 0 & A\\ B & C \end{vmatrix}=(-1)^{mn}|A||B|$

范德蒙行列式

$\begin{vmatrix} 1 & 1 & ... & 1\\ x_1 & x_2 & ... & x_n\\ x^2_1 & x^2_2 & ... & x^2_n\\ ... & ... & ... & ...\\ x^{n-1}_1 & x^{n-1}_2 & ... & x^{n-1}_n \end{vmatrix}=\prod_{1\leq i< j\leq n}(x_j-x_i),n\geq 2$

化简方案

按零多的行或列展开
用性质对差别小的行或列处理，得到零再展开
所有行和相等，则加到同一列提出公因式使得这一列全为1，再使用倍加使得这一列只有一个1
倍加处理构造零块，利用拉普拉斯展开式
爪形行列式（四种类型）消去某一个行或列转化成三角行列式

加边法（无公共规律）

目的为消去各列各个元素中某项的公共因子，第一列前面补零

递推法（高阶到低阶）

递推公式，建立n阶与n-1阶的关系，通过展开公式建立
n阶与n-1阶有着完全相似的元素分布（特别的异爪形，从并爪多的某一列或行展开）

数学归纳法（低阶到高阶）

n阶行列式证明（已经给出计算结果）

第一数学归纳法（一阶差分n阶与n-1阶关系）

验证n=1
假设n=k成立
证明n=k+1成立

第二数学归纳法（二阶差分法n阶与n-1阶以及n-2阶关系）

验证n=1、2
假设n<k成立
证明n=k成立

抽象字母型行列式计算

利用行列式性质

利用矩阵知识

C=AB，A、B为同阶方阵，则|C|=|AB|=|A||B|
C=A+B，A、B为同阶方阵，则|C|=|A+B|，做恒等变形，转化为矩阵乘积的行列式

利用题目条件（如：A A*A^T=E ）

E的妙用 $A*A^{-1}=E$

A为n阶方阵， $|A^*|=|A|^{n-1} |(A^*)^*|=||A|^{n-2}A|=|A|^{(n-1)^2}$

$\left\{\begin{matrix}|kA|^{-1}=\frac{1}{k}A^{-1},k\neq 0 \\ |kA|=k^n|A| \\ (kA)^T=kA^T \\ (kA)^*=k^{n-1}A^* \end{matrix}\right.$

用相似理论

$|A|=\prod_{i=1}^{n}\lambda _i$
若A相似于B，则|A|=|B|

矩阵	A	kA			$A^{-1}$		$P^{-1}AP$
特征值	$\lambda$	$k\lambda$	$\lambda$	$\lambda$	$\frac{1}{\lambda }$	$\frac{1}{\lambda }$	$\lambda$

$\frac{|A|}{\lambda }=\lambda ^*$

余子式和代数余子式计算

行列式展开公式

掌握原理： $A_{ij}$ 只取决于i、j的位置，而与 $A_{ij}$ 无关

总结：某一行展开后，系数灵活改变，可以凑出零行列式等特殊情况，巧妙设计未知数可以求解

使用矩阵

当 $|A|\neq0,A^*=|A|A^{-1}$ ,其中伴随矩阵为 $A^*=\begin{pmatrix} A_{11} & A_{21} & ... & A_{n1} \\ A_{12} & A_{22} & ... & A_{n2} \\ ... & ... & ... & ...\\ A_{1n} & A_{2n} & ... & A_{nn} \end{pmatrix},AA^*=|A|E$

使用特征值

$tr(A)=a_{11}+a_{22}+a_{33}=\lambda _1+\lambda _2+\lambda _3$ $A_{11}+A_{22}+A_{33}=tr(A^*)=\lambda _1\lambda _2+\lambda _1\lambda _3+\lambda _3\lambda _2$