HDU-2689 Sort it（Java实现）

Problem Description

你想通过交换两个相邻的序列元素来处理一系列n个不同的整数，直到序列按升序排列。然后它需要多少次。
例如，1 2 3 5 4，我们只需要一个操作：交换5和4。

Input

输入由许多测试用例组成。每种情况由两行组成：第一行包含一个正整数n（n <= 1000）; 下一行包含从1到n的n个整数的置换。

Output

对于每一种情况，在独立的一行内输出最少交换的次数。

Sample Input

3

1 2 3

4

4 3 2 1

Sample Output

0

6

最近想找个递归分治的题目练练，就碰到这题。该题要求将一个序列中所有相邻逆序的元素恢复成升序的序列。

方法一

最原始的方法，利用两重循环进行枚举。该算法的时间复杂度为O(n^2)，这中没什么好说的，虽简单但是效率比较低，不能通过测试。

import java.util.Scanner;
public class Main {

    public static int[] a = new int[10001];
    public static long count = 0;

    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        while(in.hasNext()) {
            int n = in.nextInt();
            for (int i = 1; i <= n; i++) {
                a[i] = in.nextInt();
            }
            count = 0;
            int i, j;
            for(i=0; i<N-1; i++)
                for(j=i+1; j<N; j++)
                    if(a[i]>a[j])
                        count++;
            System.out.println(count);
        }
    }
}

方法二

利用归并排序的思想求解逆序对的个数，这是解决该问题的一种较为高效的算法。该算法的时间复杂度为O(nlogn)。

现在假如ｎ为４，原始序列为４、３、２、１。

过程如下面所示：

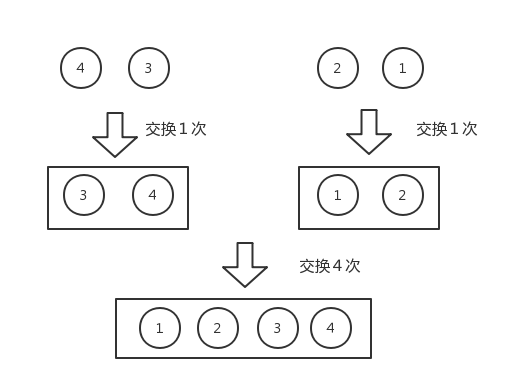
左半边是升序的，它与右边某个元素满足逆序，则它后边的元素都与右边的那个元素满足逆序，所以要交换mid-left+1次。（如：４和１，２都满足逆序，要交换两次;同理３也是）

AC代码

import java.util.Scanner;
public class Main {

    public static int[] a = new int[10001];
    public static int[] b = new int[10001];
    public static long count = 0;

    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        while(in.hasNext()) {
            int n = in.nextInt();
            for (int i = 1; i <= n; i++) {
                a[i] = in.nextInt();
            }
            count = 0;
            merge(1, n);
            System.out.println(count);
        }
    }

    public static void merge(int left,int right){
        if(left==right) return;
        int mid = (left+right)/2;
        merge(left,mid);
        merge(mid+1,right);
        int i=left,j=mid+1,k=left;
        while(i<=mid&&j<=right){
            if(a[i]>a[j]){
                b[k++] = a[j++];
                count += mid-i+1;
            }else {
                b[k++] = a[i++];
            }
        }
        while(i<=mid) b[k++] = a[i++];
        while(j<=right) b[k++] = a[j++];
        for(int x=left;x<=right;x++){
            a[x]=b[x];
        }
    }
}