牛顿迭代法

le_serein_

于 2024-03-04 23:09:08 发布

阅读量1.5k

点赞数 12

文章标签：算法线性代数机器学习

本文链接：https://blog.csdn.net/le_serein_/article/details/136465351

版权

引言

牛顿迭代法（Newton's method）又称为牛顿-拉夫逊方法（Newton-Raphson method），它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。

在数值分析中，牛顿迭代法是一种常用的求解非线性方程根的方法。它基于函数的导数和函数值的信息，通过不断迭代逼近方程的根。本文将介绍牛顿迭代法的原理、步骤以及一个简单的示例应用。

原理

牛顿迭代法的基本思想是利用函数的切线来逼近方程的根。假设我们要求解的方程 $f(x)=0$ ，从一个初始近似解 $x_{0}$ 开始，我们可以利用函数 $f(x)$ 在 $x = x_{0}$ 处的切线来估计方程的根。切线的斜率为 $f'(x_{0})$ ，所以切线与 $x$ 轴的交点就是一个新的近似解。通过不断迭代这个过程，我们可以逼近方程的根。

步骤

1.选择初始解：

选择一个合适的初始近似解 $x_{0}$ 。（初始解的选择会对最终求解结果存在一定的影响，后面将具体展开讨论）

2.计算切线交点：

计算函数 $f(x)$ 在 $x=x_{0}$ 处的函数值 $f(x_{0})$ 和导数值 $f'(x_{0})$ 。

3.更新近似解：

根据切线方程 $y = f'(x_{0})(x - x_{0}) + f(x_{0})$ 可以得到近似解 $x_{1} = x_{0} - \frac{f(x_{0})}{f'(x_{0})}$

4.判断精度：

如果满足精度要求，则停止迭代；否则，继续迭代，重复步骤 2 和步骤 3 。

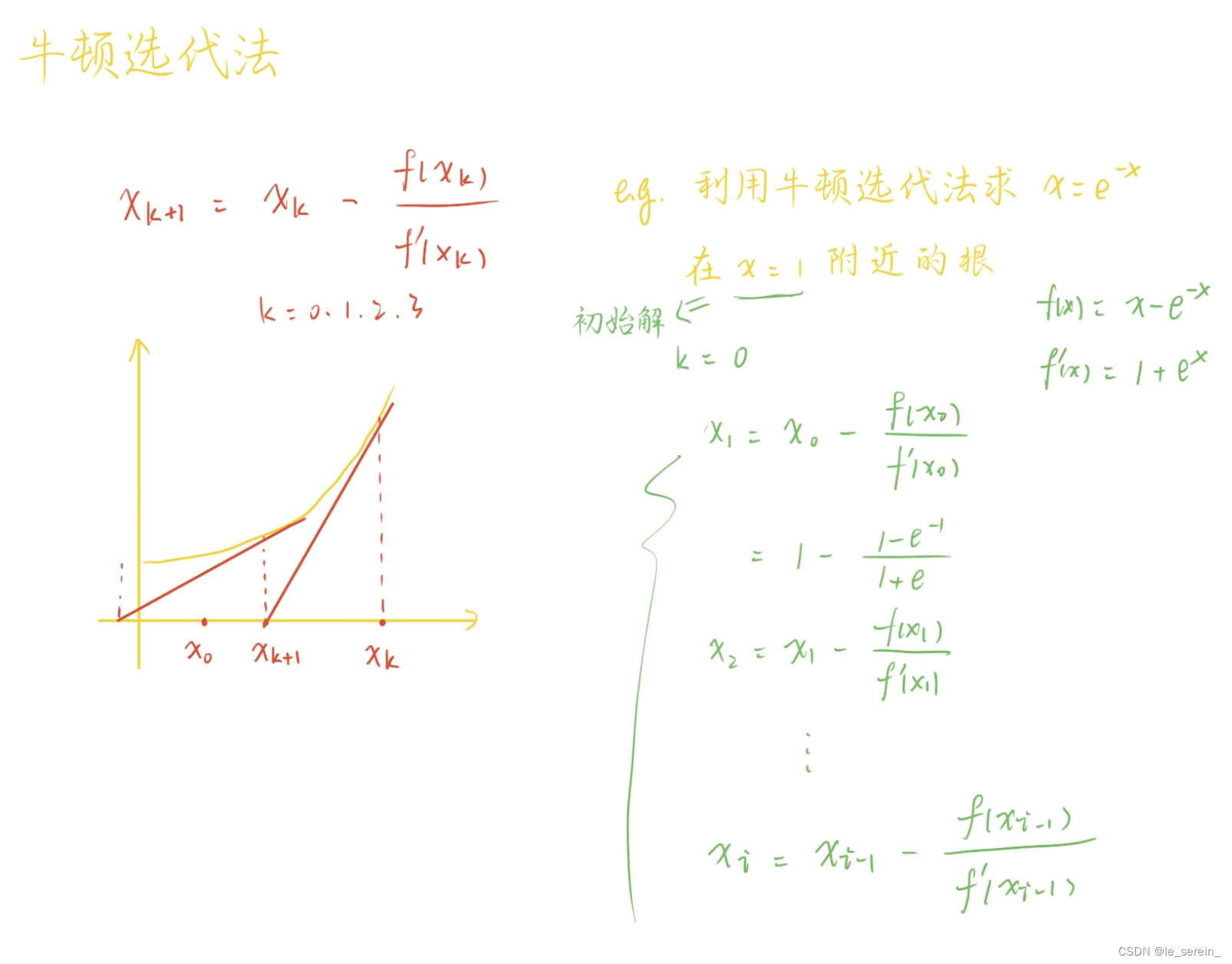
不难得到，在迭代过程中方程近似解的递推关系式为： $x_{i} = x_{i-1} - \frac{f(x_{i-1})}{f'(x_{i-1})}$

应用实例

利用牛顿迭代法求解方程 $x=e^{-x}$ 在 $x=1$ 附近的根。

%% 牛顿迭代法
clc,clear
% 利用牛顿迭代法求解 x = e^(-x) 在 x = 1 附近的根
syms x
f = x - exp(-x);
df = diff(f, x);
% 设置精度
eps = 0.0001;
% 初始解
X = zeros(1, 1000);
X(1) = 1;
% 迭代
for i = 2:1000
    X(i) = X(i - 1) - subs(f, x, X(i - 1)) / subs(df, x, X(i - 1));
    % 设置迭代终止条件
    if (abs(X(i) - X(i - 1)) < eps)
        fprintf("方程 %s = 0 的根为：%f\n", f, X(i))
        break
    end
end