第二章:
复习了一下概率论,讲了各种分布,推理过程就不写了,直接记录。
总结一下:
pmf: 概率质量函数,离散随机变量在各个特定取值上的概率。在所有实数上,包括那些X不可能等于的实数值上,都定义了 F(x)。在那些X不可能等于的实数值上,F(x)取值为0 。
cdf: 累积分布函数,连续随机变量小于或等于某个值的概率。F(x) = P(X<=x),pdf的积分。
pdf: 概率密度函数,连续随机变量在某个确定的取值点附近的可能性的函数。
联合概率:p(A,B)=p(A^B)=p(A|B)p(B),也叫积规则
边缘分布:p(A)=sum(b)p(A|B)p(B)
条件概率:p(A|B)=p(A,B)/p(B)
贝叶斯规则:p(X=x|Y=y)=p(X=x,Y=y)/p(Y=y)=p(Y=y|X=x)p(X=x)/sum(x’)P(Y=y|X=x’)p(X=x’)
独立和条件独立:
均值和方差:mean: E[x]=sum(x’)x’p(x’)(离散,连续变量是积分);
var: var[x]=E[x的平方]-u的平方
一些常见的离散分布:
1).二项(Binomial)分布:
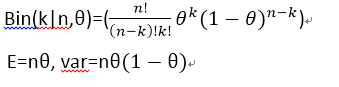
2).伯努力(Bernouli)分布:
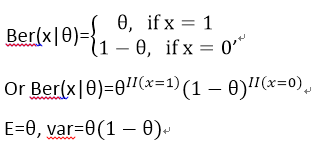
3).多项式(Multinomial)分布:
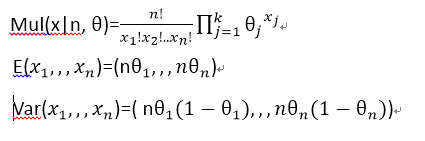
4).泊松(Poisson)分布:
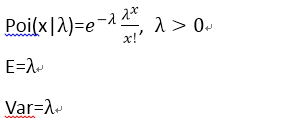
一些常见的连续分布:
1).高斯(Gaussian)分布:
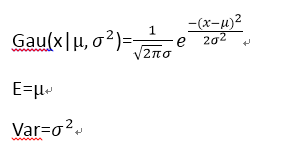
2).拉普拉斯(Laplace)分布:
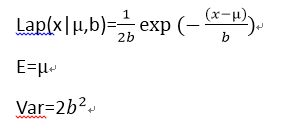
3).伽玛(Gamma)分布:
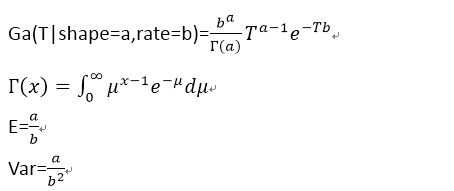
4).贝塔(Beta)分布:
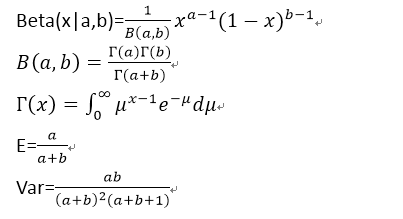
5).帕雷托(Pareto)分布:
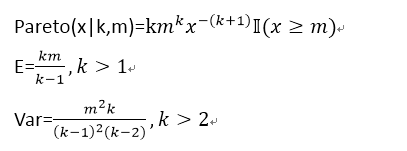
6).多变量高斯(Multivariate Gaussian)分布:
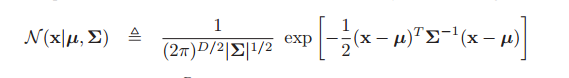
7).狄利克雷(diricilet)分布:
中心极限定理:

蒙特卡罗(Monto Carlo)近似、信息论、熵、KL散度、互信息先记着,后边会用到,再详细记录








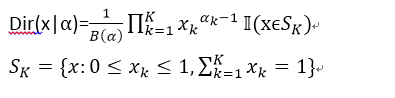

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








