考虑运输时间的分布式柔性作业车间绿色调度

引言  

      据国际能源署统计，世界能源消耗量从 2018年到 2050 年将增长近 50％，而工业部门消耗了全球一半以上的能源。在中国，制造企业消耗了全国 50%以上的电能，并产生了至少 26%的二氧化碳排放量。企业一般通过研发节能设备或采用新的加工技术缓解节能减排的压力，但是上述方法通常需要大量的投入。而绿色调度能够在不增加企业成本的情况下有效减少碳排放并提高能源效率。随着信息技术以及全球化的飞速发展，许多制造企业从传统的单工厂模式逐渐向分布式多工厂模式转变，该模式能够降低人工成本并提高生产效率。作为分布式车间调度问题的重要形式之一，分布式柔性作业车间调度问题(Distributed flexible job shop scheduling problem, DFJSP)重点关注多个柔性作业车间类型的工厂协同生产。

问题描述

DFJGSPT 可以描述为：N 个工件需要在 F 个柔性作业车间类型的工厂内加工。每个工件有 ni道工序，每个工厂有 Mf 台机器。工件需要通过运输工具在工厂以及机器之间运输。工件的加工时间，工件在机器、工厂间的运输时间以及机器的相关能耗信息已知。调度目标为最小化最大完工时间和总能耗。

假设：     (1)所有工件和机器 0 时刻可用；

                (2)每台机器同一时刻只能加工一道工序；

                (3)每个工件同一时刻只能在一台机器上加工；

                (4)不考虑中断情况；

                (5)同一工件不同工序之间有顺序约束；

                (6)有足够的运输工具完成工件的转移；

               (7)不考虑装卸载时间

 符号定义

        为方便描述，引入以下数学符号进行说明：n为工件总数；q 为加工厂总数；f 代表加工厂索引，且 f = 1，2，…，q；mf 为加工厂 f 中的机器数；k，l 代表机器索引，且 k，l = 1，2，…，mf；i 代表工件索引，且 i = 1，2，…，n；ui 为工件 i 的工序数；j 代表工序索引；r 代表加工顺序索引；Oi,j 代表工件 i 的第 j 道工序；Mf,k 代表加工厂 f 中的第 k 台机器；t~  f,k i,j代表工序 Oi,j 在机器 Mf,k 上的模糊加工时间；E~f,k,r代表机器 Mf,k 上加工的第 r 道工序的模糊开始加工时间；Qf,k 代表机器 Mf,k 上加工的工序数目；S~i,j代表工序 Oi,j 的模糊开始加工时间；C~i,j代表工序 Oi,j的模糊结束加工时间；C~i代表工件 i 的模糊完成加工时间；C~max代表最大模糊完工时间；Xf,k i,j是决策变量，若工序 Oi,j 在机器 Mf,k 上加工则为 1，否则为 0；Yf i是决策变量，若工件 i 被分配到加工厂 f 加工则为1，否则为 0；Zf,k,r i,j是决策变量，若工序 Oi,j 是机器Mf,k 上加工的第 r 道工序则为 1，否则为 0。

模型建立

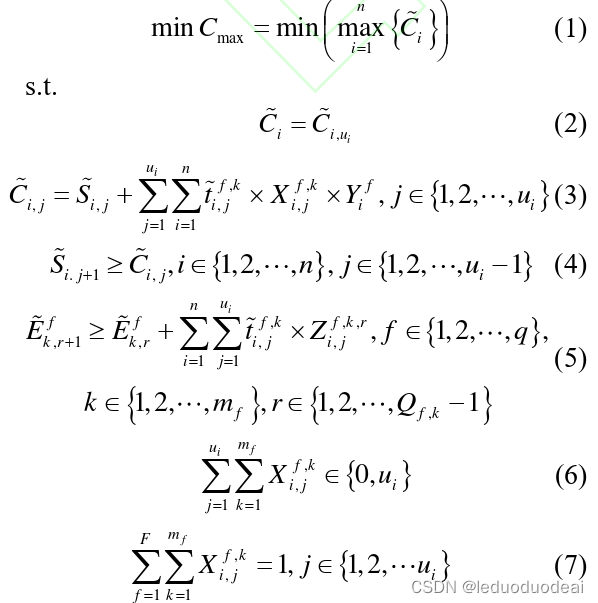
使用的算法

        NSGA-II是一种有效求解多目标优化问题的进化算法，但在求解多目标柔性作业车间调度问题时，存在早熟和易陷入局部最优的不足。本文针对 DFJGSPT 的特性，对 NSGA-II  进行改进：(1)设计了同时考虑加工时间和能耗的初始化方法以提高初始种群的质量；(2)设计了考虑运输时间的贪婪插入解码方法确定工件所分配的工厂并将染色体转换为可行有效的调度方案；(3)采用多父代交叉和新的变异方法进行种群更新；(4)设计了一种变邻域搜索策略以进一步提升 Pareto 前沿的质量。

文献来源

[1] 张洪亮,徐公杰,鲍蔷,等. 考虑运输时间的分布式柔性作业车间绿色调度_张洪亮[J]. 中国机械工程: 1-10.