PageRank算法

最新推荐文章于 2024-09-03 15:59:48 发布

legotime

最新推荐文章于 2024-09-03 15:59:48 发布

阅读量1k

点赞数

分类专栏：基础算法

本文链接：https://blog.csdn.net/legotime/article/details/51345839

版权

基础算法专栏收录该内容

5 篇文章 0 订阅

订阅专栏

PageRank算法概述

PageRank是由LarryPage命名的一个算法，它的作用是粗略的计算网页的排名。它的一个潜在假设：越重要的网

站，那么从其他网站得到的链接也越多。它在加上阻尼系数的基础上有两个公式：

$PR(A) = {1 - d \over N} + d \left( \frac{PR(B)}{L(B)}+ \frac{PR(C)}{L(C)}+ \frac{PR(D)}{L(D)}+\,\cdots \right).$ （1）

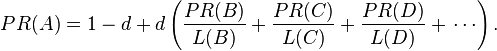$PR(A)= 1 - d + d \left( \frac{PR(B)}{L(B)}+ \frac{PR(C)}{L(C)}+ \frac{PR(D)}{L(D)}+\,\cdots \right).$ （2）

文献1说明了，Page和 Brin的公式（2）错误的把全部的网页看成是一个概率分布。所以一般用公式（1）

现在把它写成迭代的形式，如下：

$PR(p_i) = \frac{1-d}{N} + d \sum_{p_j \in M(p_i)} \frac{PR (p_j)}{L(p_j)}$ （3）

我们让：

$\mathbf{R} =\begin{bmatrix}PR(p_1) \\PR(p_2) \\\vdots \\PR(p_N)\end{bmatrix}$ （4）

那么公式就变成如下：

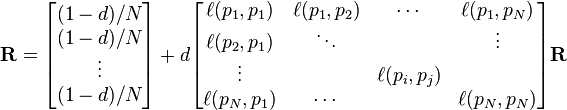$\mathbf{R} =\begin{bmatrix}{(1-d)/ N} \\{(1-d) / N} \\\vdots \\{(1-d) / N}\end{bmatrix}+ d\begin{bmatrix}\ell(p_1,p_1) & \ell(p_1,p_2) & \cdots & \ell(p_1,p_N) \\\ell(p_2,p_1) & \ddots & & \vdots \\\vdots & & \ell(p_i,p_j) & \\\ell(p_N,p_1) & \cdots & & \ell(p_N,p_N)\end{bmatrix}\mathbf{R}$ （5）

其中d是阻尼系数（默认设置为0.85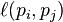）， $\ell(p_i,p_j)$ 是如果i和j没有链接，那么为0，

而且 $\sum_{i = 1}^N \ell(p_i,p_j) = 1$ （也就是说，先把之间的链接数填上，之后对列进行归一化。）

现在用过一个列子来进行说明。

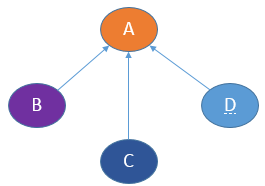
假设网页A,B,C和D关系如下：

步骤1：找出链接关系

步骤2：对列归一化

步骤3：那么 $R=[\frac{1}{4},\frac{1}{4},\frac{1}{4},\frac{1}{4}]^{T}$

下面通过matlab来进行迭代：

%迭代公式：
% R = A+d*B*R

R=[1/4;1/4;1/4;1/4];

A=[0.15;0.15;0.15;0.15]/4;

B=[0 1 1 1
    0 0 0 0
    0 0 0 0
    0 0 0 0];
for i = 1:100
    R = A +0.85*B*R;
    disp(i)
    disp(R)
end

结果：

最终的结果Pr(A)=0.1331, Pr(B)=0.0375,Pr(C)=0.0375,Pr(D)=0.0375