版权声明:本文为原创文章,未经博主允许不得用于商业用途。
Bowyer-Watson
算法原理
Bowyer-Watson算法是逐点插入算法,每次插入后分割插入点所在的三角形,如下图:

之后检查相邻三角形是否满足Delaunay三角网格条件,如果不满足则通过交换四边形对角线完成插入,如下图:

为了保持算法的连贯性,在初始时使用一个包含所有点空间的矩形和一条对角线作为初始三角网格,并在最后删除。
实现思路
这里使用Java实现了此算法。
由于三角形最多只有三个相邻三角形(共用一条边),因此可以将三角网格储存为链表结构。并且三角形需要具有外接圆属性,因此设计如下数据结构:
class mTriangle{
dPoint a;
dPoint b;
dPoint c;
dPoint center;
double Rsq;
/** share points a&b*/
int neighbor1;
/** share points b&c*/
int neighbor2;
/** share points c&a*/
int neighbor3;
public mTriangle(dPoint p1, dPoint p2, dPoint p3){
this.a = p1;
this.b = p2;
this.c = p3;
this.neighbor1 = -1;
this.neighbor2 = -1;
this.neighbor3 = -1;
center = new dPoint();
getCenter();
}
/* calculate External circle center*/
protected void getCenter(){
double A1,A2,B1,B2,C1,C2;
/* l1(b,c):A1x+B1y+C1*/
A1 = c.x-b.x;
B1 = c.y-b.y;
C1 = (-(b.y+c.y)*B1-A1*(b.x+c.x))/2;
/* l2(a,c):A2x+B2y+C2*/
A2 = c.x-a.x;
B2 = c.y-a.y;
C2 = (-(a.y+c.y)*B2-A2*(a.x+c.x))/2;
if(A1!=0 && A2!=0 && B1!=0 && B2!=0)
{
if(A1*B2==B1*A2)
{
System.out.println("Triangle error: edge parallel");
return;
}
center.y = (C1*A2-C2*A1)/(A1*B2-B1*A2);
center.x = -(B1*center.y+C1)/A1;
Rsq = dPoint.sdist(center,c);
return;
}
else
{
if((A1==0 && B1==0) || (A2==0 && B2==0))
{
System.out.println("Triangle error: same two point");
return;
}
if((A1==0 && A2==0) || (B1==0 && B2==0))
{
System.out.println("Triangle error: three points collinear");
return;
}
if(A1==0)
{
center.y = -C1/B1;
center.x = -(B2*center.y+C2)/A2;
Rsq = dPoint.sdist(center,c);
return;
}
if(A2==0)
{
center.y = -C2/B2;
center.x = -(B1*center.y+C1)/A1;
Rsq = dPoint.sdist(center,c);
return;
}
if(B1==0)
{
center.x = -C1/A1;
center.y = -(C2+A2*center.x)/B2;
Rsq = dPoint.sdist(center,c);
return;
}
center.x = -C2/A2;
center.y = -(C1+A1*center.x)/B1;
Rsq = dPoint.sdist(center,c);
return;
}
}
/* judge if p is in triangle */
public boolean inTriangle(dPoint p)
{
/* cross prod*/
dPoint MA = new dPoint(p.x - a.x,p.y - a.y);
dPoint MB = new dPoint(p.x - b.x,p.y - b.y);
dPoint MC = new dPoint(p.x - c.x,p.y - c.y);
double cp1 = MA.x * MB.y - MA.y * MB.x;
double cp2 = MB.x * MC.y - MB.y * MC.x;
double cp3 = MC.x * MA.y - MC.y * MA.x;
if(cp1>=0 && cp2>=0 && cp3>=0)
return true;
if(cp1<=0 && cp2<=0 && cp3<=0)
return true;
return false;
}
public boolean inExternalCircle(dPoint p)
{
if(dPoint.sdist(p,center)<=Rsq)
return true;
return false;
}
}
由于Bowyer-Watson算法是逐点插入的,因此实现如下插入函数,比较复杂的是如何更新三角链表,需要做多重判断:
protected void addPoint(dPoint p) {
int Tidx=0;
/* find which triangle p is in */
for(;Tidx<triangles.size();Tidx++)
if(triangles.get(Tidx).inTriangle(p))
break;
if(Tidx>=triangles.size())
{
System.out.println("addPoint error: point out of super triangles");
return;
}
mTriangle oldt = triangles.get(Tidx);
mTriangle nt1,nt2,nt3;
/* replace the old triangle by three new triangle*/
nt1=new mTriangle(oldt.a,oldt.b,p);
nt1.neighbor1 = oldt.neighbor1;
nt1.neighbor2 = triangles.size();
nt1.neighbor3 = triangles.size()+1;
// this one has no need to update
// updateNeighbor(oldt.neighbor1, Tidx, Tidx);
nt2=new mTriangle(oldt.b,oldt.c,p);
nt2.neighbor1 = oldt.neighbor2;
nt2.neighbor2 = triangles.size()+1;
nt2.neighbor3 = Tidx;
updateNeighbor(oldt.neighbor2, Tidx, triangles.size());
nt3=new mTriangle(oldt.c,oldt.a,p);
nt3.neighbor1 = oldt.neighbor2;
nt3.neighbor2 = Tidx;
nt3.neighbor3 = triangles.size();
updateNeighbor(oldt.neighbor3, Tidx, triangles.size()+1);
triangles.set(Tidx,nt1);
triangles.add(nt2);
triangles.add(nt3);
if(needUpdate(Tidx,nt1.neighbor1))
updateQuadrilateral(Tidx,nt1.neighbor1);
else if(needUpdate(triangles.size()-2,nt2.neighbor1))
updateQuadrilateral(triangles.size()-2,nt2.neighbor1);
else if(needUpdate(triangles.size()-1,nt3.neighbor1))
updateQuadrilateral(triangles.size()-1,nt3.neighbor1);
}
在完成算有点插入后需要删除和初始化使用的矩形有关的三角网格
protected void deleteSuperTriangle() {
for(int i=0,len=triangles.size();i<len;i++){
if(useSuperTrianglePoints(i))
{
triangles.remove(i);
--len;
--i;
}
}
}
因此算法的完整流程为:
mTriangle t1 = new mTriangle(superp1,superp2,superp4);
mTriangle t2 = new mTriangle(superp2,superp3,superp4);
t1.neighbor2=1;
t2.neighbor3=0;
triangles.add(t1);
triangles.add(t2);
for(dPoint x:pointlist)
addPoint(x);
deleteSuperTriangle();
效果示例
以添加四个点为例,下图为网格更新的流程
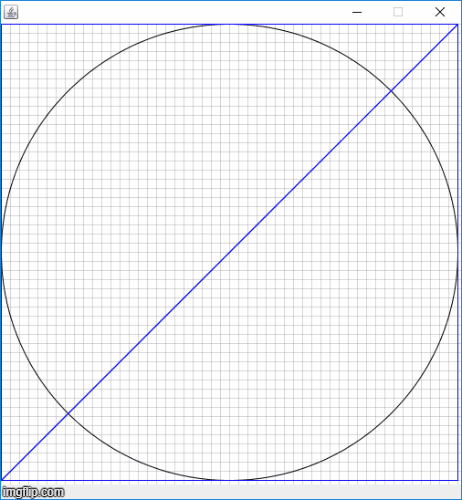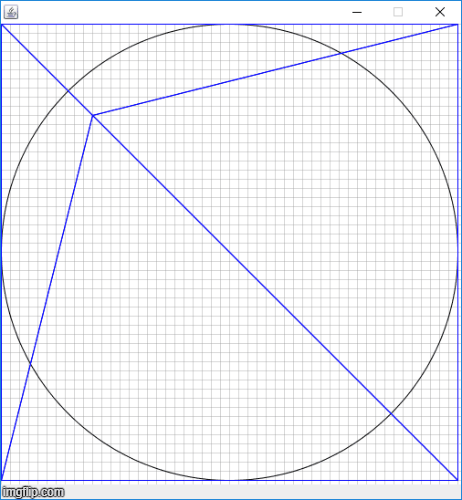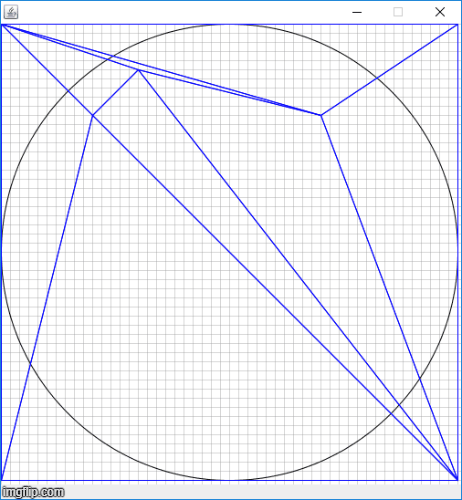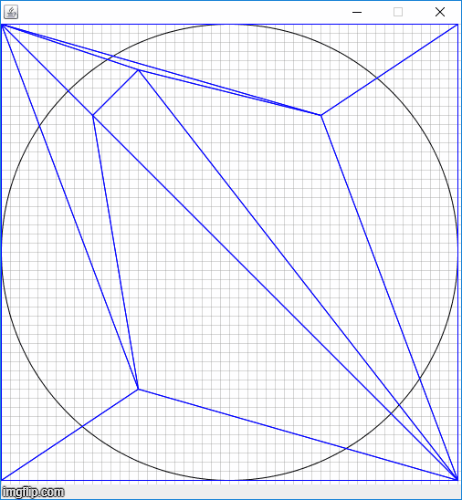
完整代码见github
























 222
222











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








