微软2014实习生在线测试之k-th string

Description

Consider a string set that each of them consists of {0, 1} only. All strings in the set have the same number of 0s and 1s. Write a program to find and output the K-th string according to the dictionary order. If such a string doesn’t exist, or the input is not valid, please output “Impossible”. For example, if we have two ‘0’s and two ‘1’s, we will have a set with 6 different strings, {0011, 0101, 0110, 1001, 1010, 1100}, and the 4th string is 1001.

Input

The first line of the input file contains a single integer t (1 ≤ t ≤ 10000), the number of test cases, followed by the input data for each test case.
Each test case is 3 integers separated by blank space: N, M(2 <= N + M <= 33 and N , M >= 0), K(1 <= K <= 1000000000). N stands for the number of ‘0’s, M stands for the number of ‘1’s, and K stands for the K-th of string in the set that needs to be printed as output.

Output

For each case, print exactly one line. If the string exists, please print it, otherwise print “Impossible”.

样例输入

3
2 2 2
2 2 7
4 7 47

样例输出

0101
Impossible
01010111011
#include<iostream>
#include<string>
using namespace std;
#define MAXLEN 33
/***********************************************************
*功能描述：获取N个0和M个1的所有组合数
*输入：n:0的个数
			 m:1的个数
*返回值：组合数
************************************************************/
long long getSum(long long n,long long m)
{
	long long sum=1,divide=1;
	long long big=n+m;
	long long small = n; 
	for(int i = 0;i < n; i++)
	{
		sum*=big;
		big--;
		divide*= small;
		small--;
	}
	return sum/divide;
}

/************************************************************************
*功能描述：构造N个0和M个1组合初值（即组合中最小的值）
*输入：n:0的个数
			 m:1的个数
*返回值：组合数
*************************************************************************/
void initData(char *p,long long N,long long M)
{
	int i=0;
	for(;i < M;i++)
		p[i] = '1';
	for(;i < N+M; i++)
		p[i] = '0';
}

/************************************************************************
*功能描述：保证0和1的个数不变的基础上，值每次递增1
*输入：data:组合数组
            sum:组合位长
*返回值：组合数
*************************************************************************/
void addBit(char *p,long long sum)												//递增一次
{
	for(int i = 0;i < sum-1; i++)
	{
		if(p[i]=='1'&&p[i+1]=='0')					
		{
			p[i+1]='1';
			p[i] = '0';											//将该位以后的值变成最小：低位的0与高的1进行交换
			for(int j = i-1; j >= 1;j-- )					//从高位开始找最近的一个1
			{
				if(p[j]=='1')									 //找到高位的一个1
				{
					for(int k=0;k < j;k++)				 //从低位开始探索1个0
					{
						if(p[k] == '0')						//进行交换
						{
							p[j] = '0';
							p[k] = '1';
							break;
						}		
					}
				}
			}
			return;
		}
	}
}

/************************************************************************
*功能描述：显示组合结果
*输入：p:组合存放数组，sum:组合位长
*返回值：无
*************************************************************************/
void display(char *p,long long sum)
{
	for(long long i = sum-1;i >= 0;i--)
		cout<<p[i];
	cout<<endl;
}

int main()
{
	int caseN;
	char data[MAXLEN];
	long long all;
	long long N,M,K;
	long long value=0;
	cin>>caseN;
	while(caseN)
	{
		value = -1;  
		cin>>N>>M>>K;
		all = getSum(N,M);
		if(K > all)											//判断K值是否超过总组合数
			cout<<"Impossible"<<endl;
		else
		{
			initData(data,N,M);
			for(int i = 0; i < K-1;i++)
			{
				addBit(data,N+M);
			}
			display(data,N+M);	
		}
		caseN--;
	}
	return 0;
}
这是我的思路，为了保证0，1的个数不变，求第k个string串，关键就是如何求得最小的递增addBit()。找最小递增组合值步骤：（1）从低位向高位找第一个01XXXXX,变换成10XXXXX.因为只有这样增加，首先是保证了0，1的个数不变。（2）为了保证是最小的增量，就需要把后面的xxxxx中，高位的1与低位的0进行交换。也就是把后的值换成最小的值。然后求第K个string.递增K-1次后的串就是我们想要的串。

这里实现有点浪费空间了，后面可以尝试用一个long long 型值来替代data[]数组

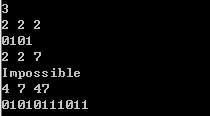
测试结果：