一、什么是跳表
跳表全称叫做跳跃表,简称跳表。跳表是一个随机化的数据结构,可以被看做二叉树的一个变种,它在性能上和红黑树,AVL树不相上下,但是跳表的原理非常简单,目前在Redis和LeveIDB中都有用到。
在对有序顺序表进行搜索时,使用二分查找时间复杂度是O(logn),但是有序顺序表的插入和删除却是O(n)的算法。
在对有序链表进行搜索时,时间复杂度是O(n),但是对链表的插入算法却是O(1)。
可以看到有序顺序表和链表各有各的优势,同时也有自身的缺点,而我们要讲的跳跃表就是集成了以上两种数据结构的优点,但是自身多耗费一部分空间的数据结构。
二、跳表的原理
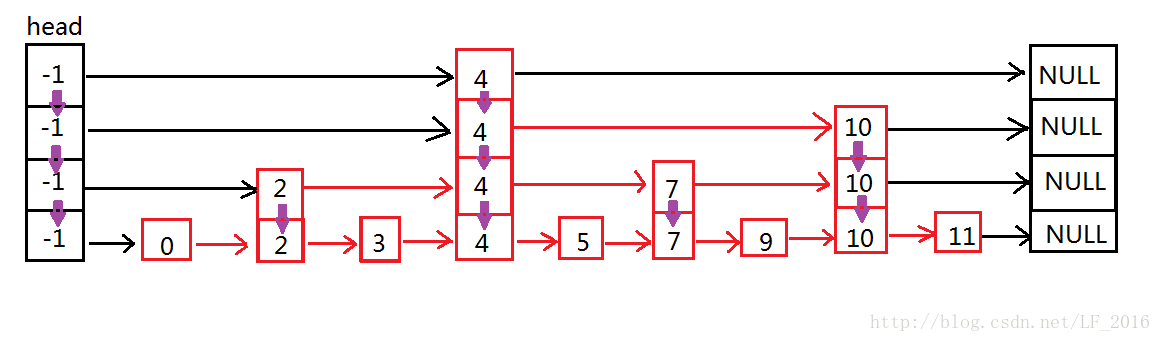
跳表的原理非常简单,跳表其实就是一种可以进行二分查找的有序链表。跳表的数据结构模型如图:
可以看到,跳表在原有的有序链表上面增加了多级索引,通过索引来实现快速查找。首先在最高级索引上查找最后一个小于当前查找元素的位置,然后再跳到次高级索引继续查找,直到跳到最底层为止,这时候以及十分接近要查找的元素的位置了(如果查找元素存在的话)。由于根据索引可以一次跳过多个元素,所以跳查找的查找速度也就变快了。
最理想的情况下,跳表就像一颗满二叉树,查找的时间复杂度是O(logn)。问题 是怎么决定一个结点有多少级索引???
针对这个问题跳表的创始人提出了一种抛硬币的方法,用随机函数产生一个0或者1,如果是1的话则leve++,直到产生0位置,当数据量足够大的时候,leve的取值会趋向于正态分布。
三、跳表与红黑树,AVL树等平衡数据结构的比较
跳表与红黑树和AVL树相比,效率不相上下,但是它胜在实现起来比较简单,我们可以很快的实现出来。跳表在更新的时候需要改动的地方很少,而红黑树和AVL树需要改动的地方很多。如果在多线程的情况下,红黑树和AVL树在维持平衡的时候,需要的锁资源很多,越是在靠近根节点的地方越容易产生竞争。但是跳表的操作更加局部性一点,需要锁住的资源很少。
四、跳表的实现
跳表的性质:
1、由很多层组成
2、每一层都是一个有序链表
3、最底层的链表包含所有元素
4、如果一个元素出现在第i层的链表中,则它在i-1层中也会出现。
5、上层节点可以跳转到下层。
跳表的实现:
#ifndef _SKIPLIST_H__
#define _SKIPLIST_H__
#include<time.h>
#include<iostream>
#include<vector>
#include<cstdio>
#include<cstdlib>
using namespace std;
#define MAXLEVE 8 //跳表的最大层数
template<typename K,typename V>
struct SkipNode //跳表的节点类型
{
K _key;
V _value;
size_t _sz; //表示该节点的层数
vector<SkipNode<K,V> *> _pleve; //存放每一层的指针
SkipNode(K key=K(),V value=V(),size_t sz=size_t())
:_key(key)
,_value(value)
,_sz(sz)
{
_pleve.resize(0);
for(size_t i=0;i<sz;i++)
{
_pleve.push_back(NULL);
}
}
~SkipNode()
{
_key=-1;
_value=-







 跳表是一种随机化的数据结构,结合了有序顺序表和链表的优点,允许高效的搜索、插入和删除操作。它通过在原有有序链表上增加多级索引实现快速查找,时间复杂度为O(logn)。跳表的创始人提出了用随机函数决定节点的索引级别,以达到平衡。相比红黑树和AVL树,跳表实现简单,更新时改动小,适合多线程环境。
跳表是一种随机化的数据结构,结合了有序顺序表和链表的优点,允许高效的搜索、插入和删除操作。它通过在原有有序链表上增加多级索引实现快速查找,时间复杂度为O(logn)。跳表的创始人提出了用随机函数决定节点的索引级别,以达到平衡。相比红黑树和AVL树,跳表实现简单,更新时改动小,适合多线程环境。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 906
906

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








