正态分布/BP算法—笔记

1.为什么正态分布在自然界如此常见？

（1）n个独立同分布随机变量，根据中心极限定律，当n趋于无穷时，其平均值服从正太分布（高斯分布）。一个指标受到若干因素影响，但是单个因素又对指标构不成决定性影响，则该指标服从中心极限定律，收敛与正太分布——林徳伯格-费勒中心极限定理。

（2）正太分布的信息墒最大

（3）统计学三大分布：卡方分布，t分布，f分布都与正太分布有关

（4）Everyone believes in the normal law, the experimenters because they imagine that it is a mathematical theorem, and the mathematicians because they think it is an experimental fact——法国物理学家

（5）自然界最常见的分布并不是正太分布，而是长尾分布。自然界的各个变量之间往往是有关系的。

2. backpropagation

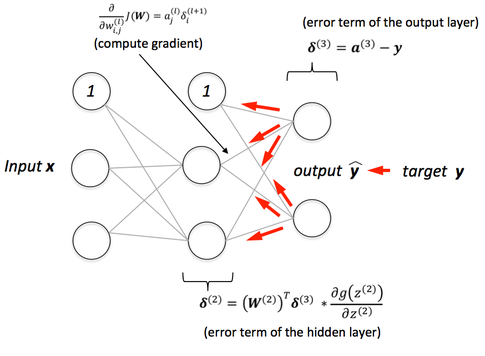
本质：通过改变网络权重（参数）来改变目标损失函数，最终转换为计算损失函数对权重的梯度，而损失函数对权重梯度公式最终由残差来表示。

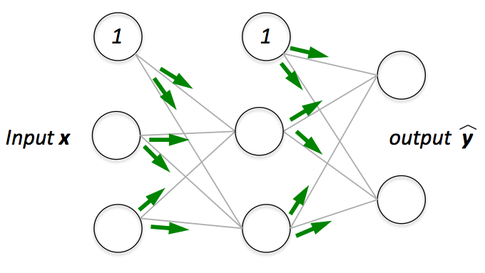
（1）forward propagation：输入训练数据，结合对应权值和激活函数，传遍整个网络，最后获得输出。计算：矩阵×矩阵 ，...，矩阵x矩阵，矩阵x向量

（2）back propagation：根据网络输出的预测值和真实值获得惨差，把残差反向传遍整个网络（表现为各个权值的梯度）。计算：向量x矩阵，...，向量x矩阵——更高效！梯度的具体计算

方法是：利用多元函数求导的链式法则。