深度学习：自编码器、神经网络基础

基本的自编码器（Autoencoder）是一个含有输入、隐含、输出的三层神经网络，它的目的是尽可能复现输入输出的关系。

一. 神经元

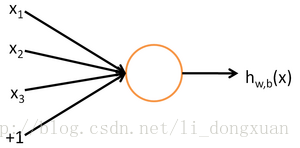
神经网络的最小组成单元是神经元，神经元的结构如下：

左边的$x_1,x_2,x_3$是运算输入值，$1$代表截距（为什么要有截距：我们知道线性拟合的时候如果不含常数项即截距，那么无论怎么拟合数据都必将经过原点，这很有可能和实际数据不符，在神经网络里也是这个原因）。

接着每个由输入到中间的那个圆圈的各条箭头线都附有权值$W$（长度等于输入个数+截距个数1）。

中间的圆圈代表激活函数$f(\cdot)$，通常有s激活函数（sigmoid，取值范围0~1）和双曲正切函数（tanh，取值范围-1~1）。

最后的$h(x)$代表输出：

$$h_{W,b}(x)=f(W^Tx)=\sum_{i=1}^{3}W_ix_i+b$$

二. 神经网络结构

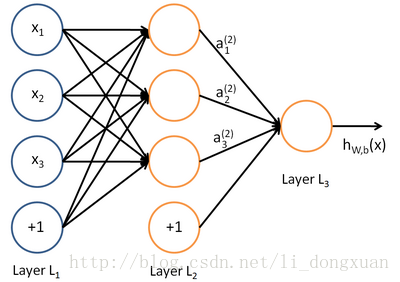
最基本的神经网络由输入、隐含、输出三层结构组成，如下图：

除了最后一层输出层，每一层的数据都包含额外的一项偏置结点，也就是之前说的截距。每一条带箭头的直线都代表一个权值（$h(x)$后的那条除外）。黄色的圈都代表对他的所有直接输入数据的加权和的激活处理。

从第一层开始向后一步一步进行加权和激活运算，这个过程叫做前向传播。合理的神经网络会尽可能拟合现有数据的输入输出关系，而要想达到这一目的，我们需要找到每一层网络上的合适的权重$W$，这一求解过程的方法就是反向传播算法。

三. 反向传播算法（Backpropagation，BP）

首先我们要设定一个代价函数来评价神经网络求解结果的好坏，和线性拟合的代价函数类似，都是二次损失。整体的代价函数如下：

$$J(W,b)=\frac{1}{m}\sum_{i=1}^m(\frac{1}{2}\|h_{W,b}(x^{(i)})-y^{(i)}\|^2)+\frac{\lambda}{2}\sum_{l}\sum_{i}\sum_{j} (W_{ji}^{(l)})^2$$

$m$是数据里有$m$个样例。

那么这里为什么要多一规则项（也称权重衰减项）$\frac{\lambda}{2}\sum_{l}\sum_{i}\sum_{j} (W_{ji}^{(l)})^2$呢：

因为我们为了稳定性要限制$W$的大小（一个稳定性解释的例子），必须添加一个关于的$W$的限制条件，也就是要使$\sum_{k=1}W_k^2\leqslant$某个常数。记得我们在本科时期学习的求解带有约束条件的目标函数的最优值吗？是的，那就是在原来的目标函数上添加约束条件的表达式。

$\lambda$是权重衰减参数，用于控制公式中两项的相对重要性。

我们的目标是针对参数$W$和$b$来求其函数$J(W,b)$的最小值。为了求解神经网络，我们需要将每一个参数$W^{(l)}_{ij}$和$b^{(l)}_i$初始化为一个很小的、接近零的随机值（比如说，使用正态分布${Normal}(0,\epsilon^2)$生成的随机值，其中$\epsilon$设置为0.01，之后对目标函数使用诸如批量梯度下降法的最优化算法。因为$J(W, b)$是一个非凸函数，梯度下降法很可能会收敛到局部最优解；但是在实际应用中，梯度下降法通常能得到令人满意的结果。

需要再次强调的是，要将参数进行随机初始化，而不是全部置为0。如果所有参数都用相同的值作为初始值，那么所有隐藏层单元最终会得到与输入值有关的、相同的函数。

梯度下降法的本质其实就是迭代求编导数：

$$\begin{align} W_{ij}^{(l)} &= W_{ij}^{(l)} - \alpha \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b) \\ b_{i}^{(l)} &= b_{i}^{(l)} - \alpha \frac{\partial}{\partial b_{i}^{(l)}} J(W,b) \end{align}$$

其中$\alpha$是学习速率。其中关键步骤是计算偏导数。反向传播算法是计算偏导数的一种有效方法，反向传播算法具体步骤如下：

（1）进行前馈传导计算，利用前向传导公式，得到$L_2, L_3, \ldots$直到输出层$L_{n_l}$的激活值

（2）对于第$n_l$层（输出层）的每个输出单元$i$，我们根据以下公式计算残差：

$$\begin{align} \delta^{(n_l)}_i = \frac{\partial}{\partial z^{(n_l)}_i} \;\; \frac{1}{2} \left\|y - h_{W,b}(x)\right\|^2 = - (y_i - a^{(n_l)}_i) \cdot f'(z^{(n_l)}_i) \end{align}$$

（3）对$l = n_l-1, n_l-2, n_l-3, \ldots, 2$的各个层，第$l$层的第$i$个节点的残差计算方法如下：

$$\delta^{(l)}_i = \left( \sum_{j=1}^{s_{l+1}} W^{(l)}_{ji} \delta^{(l+1)}_j \right) f'(z^{(l)}_i)$$

以上逐次从后向前求导的过程即为“反向传导”的本意所在

（4）计算我们需要的偏导数，计算方法如下：

$$\begin{align} \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b; x, y) &= a^{(l)}_j \delta_i^{(l+1)} \\ \frac{\partial}{\partial b_{i}^{(l)}} J(W,b; x, y) &= \delta_i^{(l+1)} \end{align}$$

反向传播是批量梯度下降中的重要一步，上述公式的具体推导可以看这里 。

现在给出批量梯度下降中的一次完整迭代：

（1）对于所有$l$，令 $\Delta W^{(l)} := 0$, $\Delta b^{(l)}:= 0$（设置为全零矩阵或全零向量，零元素为一个很小的、接近零的随机值）

（2）对于$i = 1$到$m$，

①使用反向传播算法计算 $\nabla_{W^{(l)}} J(W,b;x,y)$和$\nabla_{b^{(l)}} J(W,b;x,y)$

②计算 $\Delta W^{(l)} := \Delta W^{(l)} + \nabla_{W^{(l)}} J(W,b;x,y)$

③计算$\Delta b^{(l)} := \Delta b^{(l)} + \nabla_{b^{(l)}} J(W,b;x,y)$

（3）更新权重参数：

$$\begin{align} W^{(l)} &= W^{(l)} - \alpha \left[ \left(\frac{1}{m} \Delta W^{(l)} \right) + \lambda W^{(l)}\right] \\ b^{(l)} &= b^{(l)} - \alpha \left[\frac{1}{m} \Delta b^{(l)}\right] \end{align}$$

现在，我们可以重复梯度下降法的迭代步骤来减小代价函数$J(W,b)$的值，进而求解我们的神经网络。求解结束以后就可以用来预测数据了。

四.参考资料

UFLDL教程