N-C型数值积分中Richardson外推加速法及其应用

摘 要

本文探讨了N-C型数值积分中Richardson外推加速法的理论基础、具体实施步骤及其在实际问题中的应用。文章首先简单介绍N-C型数值积分了的基本数学思想，随后详细解释了Richardson外推加速法的概念和步骤，包括选择初始步长、计算数值积分结果并详细展示如何进行外推以提高精度。通过理论分析推导和简单举例验证，本文展示了Richardson外推加速法相较于梯形法则和细化步长法如何显著提升数值积分的精度。这种方法在数值积分领域展现出巨大潜力，为解决此类复杂问题提供了有效的工具。

一 引 言

数值积分是数值分析的一个重要分支，用于计算定积分的近似值，常见的数值积分方法有梯形法则、辛普森(Simpson)法等。然而，这些方法的精度受限于步长的选择。为了提高积分精度，Richardson外推加速法被提出且广泛运用于数值积分以及其他需要提高计算精度的场景中。本文主要讨论Richardson外推加速法在N-C型数值积分方法中的应用。

二 Richardson外推加速算法原理

N-C型数值积分方法是一种高精度的数值积分方法，通过组合梯形法则和辛普森法则来提高积分精度。其基本思想是在不同的步长下分别应用梯形法则和辛普森法则，然后通过线性组合来消除低阶误差项。

假设我们有一个数值积分方法T(h)，其中h为步长，如果我们已知此方法的误差形式如下：  

其中系数a(k)(k=1,2,)与h无关.

通过改变步长h(比如取h和h/2）,我们可以得到不同的近似值T(h)和T(h/2)。它们的误差分别为E(h)和E(h/2)根据误差的形式，我们可以写出：

为了消除误差项，我们利用这两个数值解来构造一个新的数值解T1(h)，使得的精度高于T(h)和T(h/2)：

这个表达式消除了项h2误差，同时此结果也是梯形法则的Richardson外推法运算结果从而得到

根据如上公式可得

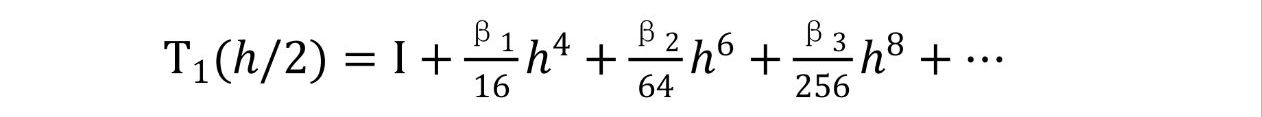
若令

则可以进一步消去项h4的误差，从而有

同理得  

经过m(m=1,2,)次加速后，余项便取以下形式：

上述处理方法通常称为Richardson外推加速法。

三 问题分析及Python代码实现

关于Richardson外推加速法在数值分析的应用实例：

示例一：指数型函数积分

假设我们要计算在区间上的积分

第一步：

假设初始步长为h=0.1，分割点数n=10

def composite_trapezoidal(f, a, b, n):

    h = (b - a) / n

    x = [a + i * h for i in range(n+1)]

    integral = 0.5 * f(a) + 0.5 * f(b)

    for i in range(1, n):

        integral += f(x[i])

    return integral * h

import math

def f(x):

    return math.exp(-x**2)

a, b = 0, 1

initial_step = 0.1

T_h = composite_trapezoidal(f, a, b, int((b-a)/initial_step))

print("初始步长下的积分结果:", T_h)

由python运行可得结果为

第二步：

减少步长并计算新的运算结果，此时设步长h=0.05，则分割点数n=20

new_step = 0.05

T_h2 = composite_trapezoidal(f, a, b, int((b-a)/new_step))

print("更细步长下的积分结果:", T_h2)

运行得到结果

第三步：

运用Richardson外推法

def richardson_extrapolation(T_h, T_h2):

    return (4 * T_h2 - T_h) / 3

I_star = richardson_extrapolation(T_h, T_h2)

print("经过Richardson外推后的积分结果:", I_star)

运行得到以下结果

示例二：多项式型函数积分

假设我们要计算在区间上的积分

参照示例一的步骤进行重复操作得到下图结果

为了展示Richardson外推法相对于直接使用梯形法则的优势，我们编写了一个Python脚本来比较两种方法的精度和收敛速度。我们将使用同一个积分问题，并分别使用梯形法则和Richardson外推法来计算积分值，然后绘制出误差随步长变化的图。

import numpy as np

import matplotlib.pyplot as plt

from scipy.integrate import trapezoid

from scipy.special import erf

# 定义被积函数

def f(x):

    return np.exp(-x**2)

# 定义积分区间

a = 0

b = 1

# 设置步长范围

N_range = np.arange(1, 16)

# 计算梯形法则的积分值及其误差

trapz_results = np.zeros(len(N_range))

trapz_errors = np.zeros(len(N_range))

for i in range(len(N_range)):

    n = 2**N_range[i]

    x = np.linspace(a, b, n + 1)

    trapz_results[i] = trapezoid(f(x), x)

    exact_integral = (np.sqrt(np.pi) * (erf(b) - erf(a))) / 2 # 精确解

    trapz_errors[i] = abs(trapz_results[i] - exact_integral)

# 使用Richardson外推法计算积分值及其误差

richardson_results = np.zeros(len(N_range))

richardson_errors = np.zeros(len(N_range))

for i in range(len(N_range)):

    n = 2**N_range[i]

    x = np.linspace(a, b, n + 1)

    integral = trapezoid(f(x), x)

    # 进行Richardson外推

    for k in range(2, i + 2):

        prev_integral = richardson_results[i - (k - 1)] if i >= (k - 1) else trapz_results[i - (k - 1)]

        integral = (4**(k-1) * integral - prev_integral) / (4**(k-1) - 1)

    richardson_results[i] = integral

    richardson_errors[i] = abs(richardson_results[i] - exact_integral)

# 绘制误差随步长变化的图

plt.figure()

plt.semilogy(N_range, trapz_errors, 'r-o', label='Trapezoidal Rule')

plt.semilogy(N_range, richardson_errors, 'b-x', label='Richardson Extrapolation')

plt.xlabel('Step Size (2^-N)')

plt.ylabel('Absolute Error')

plt.title('Comparison of Trapezoidal Rule and Richardson Extrapolation')

plt.legend()

plt.grid(True)

plt.show()

# 打印最终误差

print(f'最终误差（梯形法则）: {trapz_errors[-1]:.15f}')

print(f'最终误差（Richardson外推）: {richardson_errors[-1]:.15f}')

生成结果如图

 

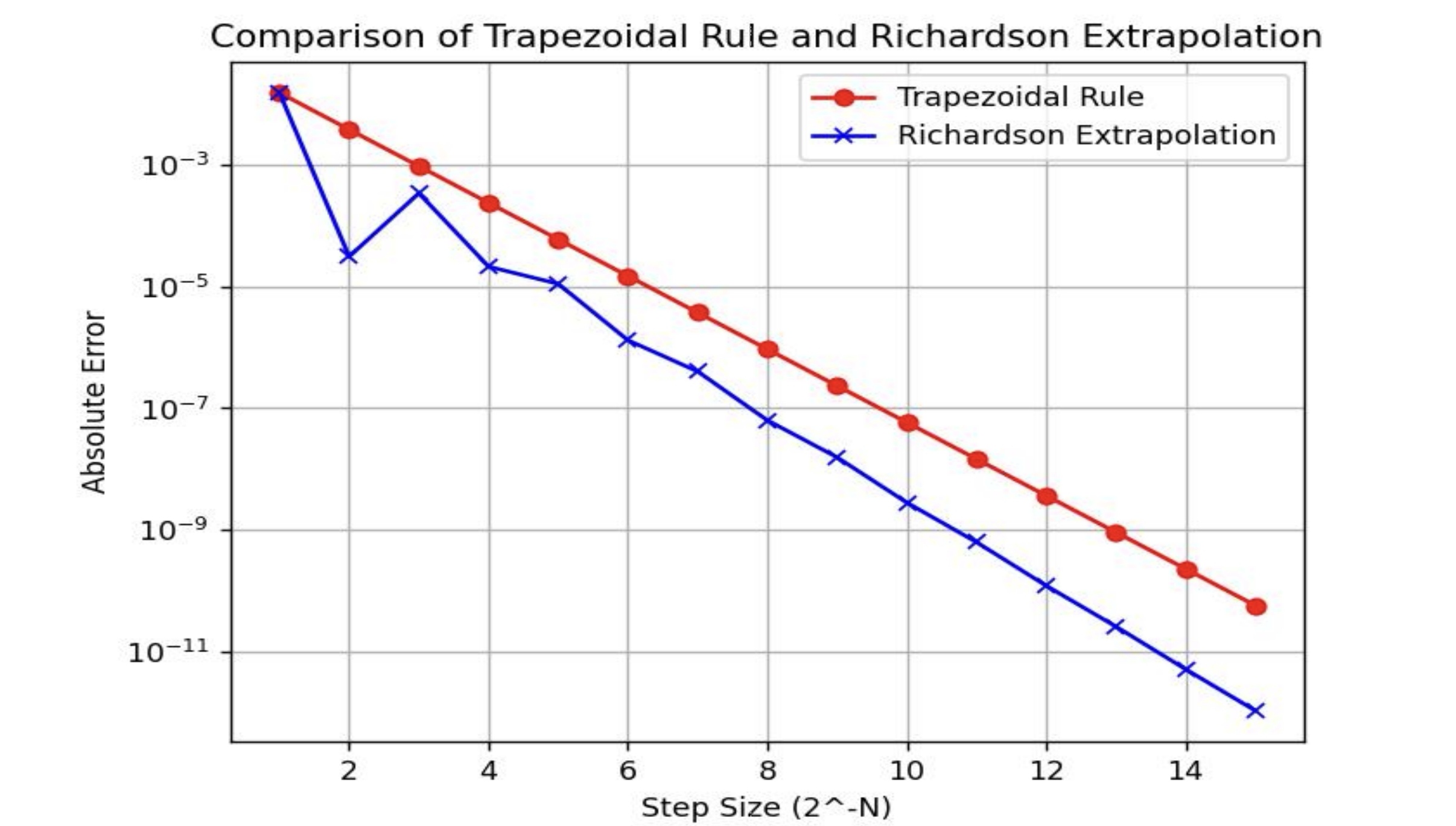
通过以上图表，我们可以直观地看到Richardson外推法在提高积分精度方面的优势。可以看到，随着步长减小，Richardson外推法的误差收敛更快。这种方法不仅可以应用于数值积分，还具有广泛的适用性，可以在其他需要提高计算精度的数值计算场景中使用。

 

四 结果分析及总结

通过示例一的数值运算结果

以及示例二的数值运算结果

我们不难发现，由细化步长和Richardson外推法得到的积分值往往比原始的梯形法则在粗略步长下得出的近似值更加接近实际值。由结果看出，细化步长和Richardson外推法显著提高了积分的精度。

Richardson外推加速算法通过利用不同步长下的计算结果来构造更高精度的逼近公式，是一种非常有效的提高数值计算精度的方法。这种方法在数值积分、微分方程求解等多个领域都有广泛的应用。