大卖网逆向分析params参数之加密算法分析

已于 2023-11-25 09:51:26 修改
阅读量2.7k 收藏 10
点赞数 1
CC 4.0 BY-SA版权
分类专栏： 逆向 文章标签： 爬虫
于 2023-08-11 11:00:23 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/liberty888/article/details/132226466
文章主要分析APP加密算法，先通过jadx打开APK找到加密类，因b方法无可读性，再用JEB打开转化为有一定可读性的伪代码。经分析发现使用android.util.Base64.encodeToString加密，通过复制类到JAVA环境测试，按JEB代码逻辑处理后加密结果与APP一致。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

在之前文章已经找到了params参数的生成位置，这里分析下加密算法

使用jadx打开APK，打开加密类，如下

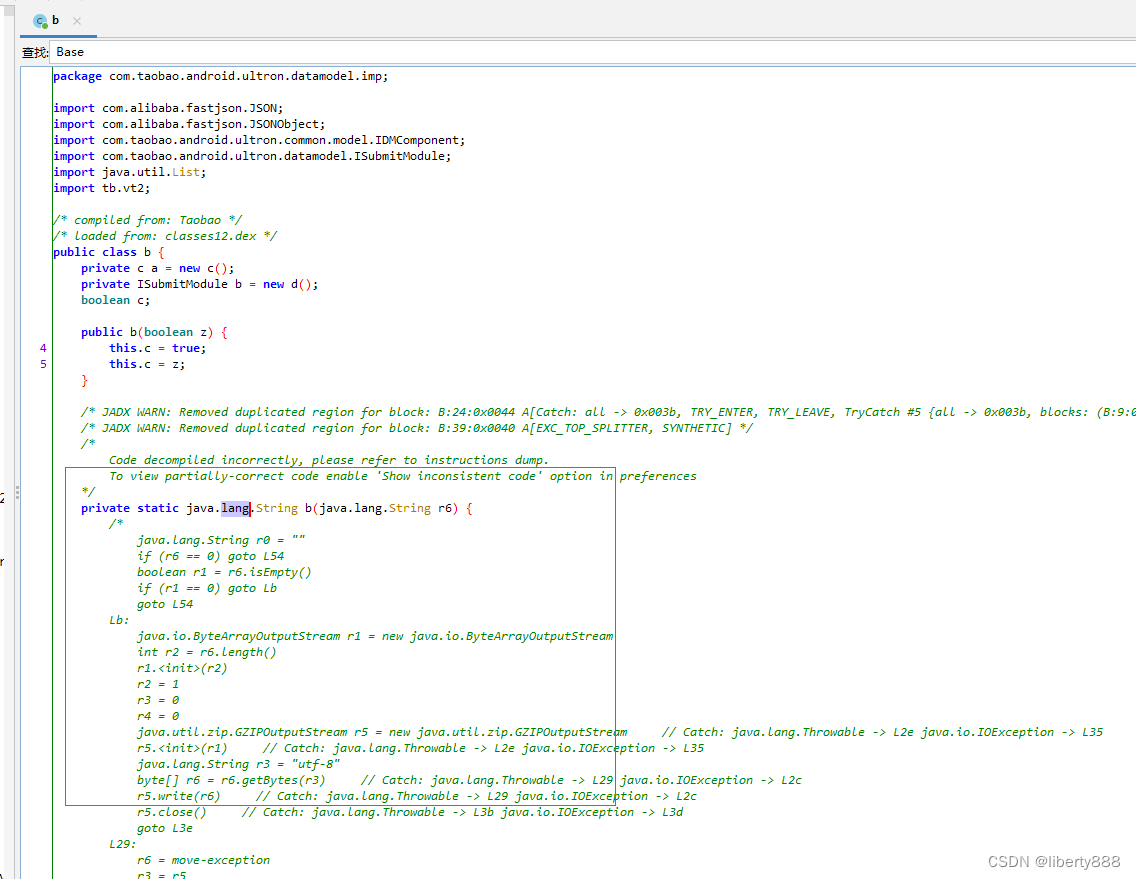
 发现这个b方法没有可读性，使用JEB打开，如下

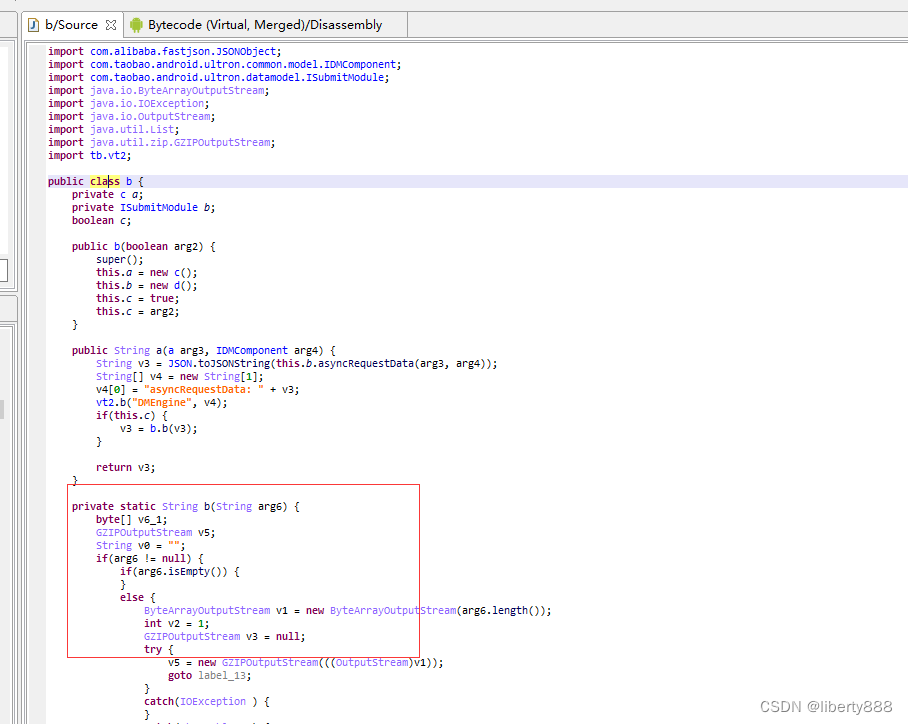
 按TAB转化下，发现具有一定可读性，但是也是伪代码，代码直接扔到JAVA里是跑不起来的。

稍微分下可以得到使用了android.util.Base64.encodeToString(v6_1, 0);加密，注意这里的v6_1和入参arg6是不一样的，将android.util.Base64这个类复制到JAVA环境测试下，如下

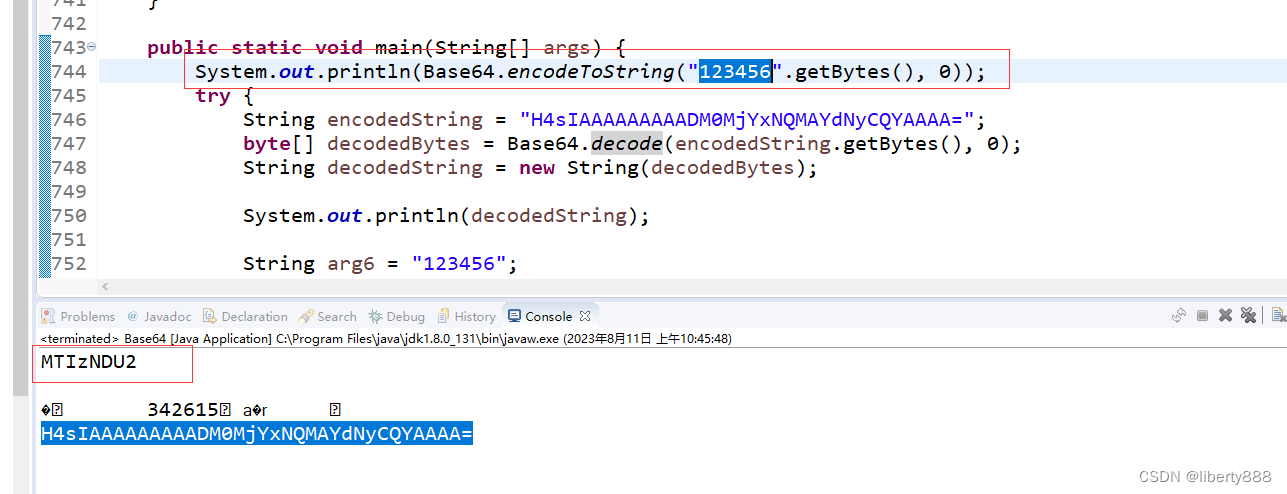
'123456'签名出来是MTIzNDU2，实际应该是H4sIAAAAAAAAADM0MjYxNQMAYdNyCQYAAAA=

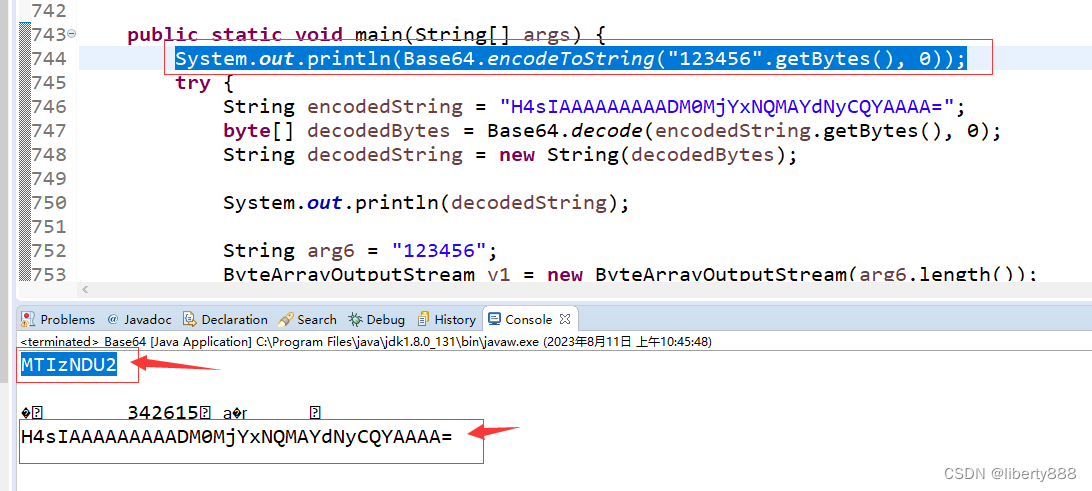 这个b方法对入参进行了处理后再base64加密导致，照着JEB里面代码逻辑扣下，如下

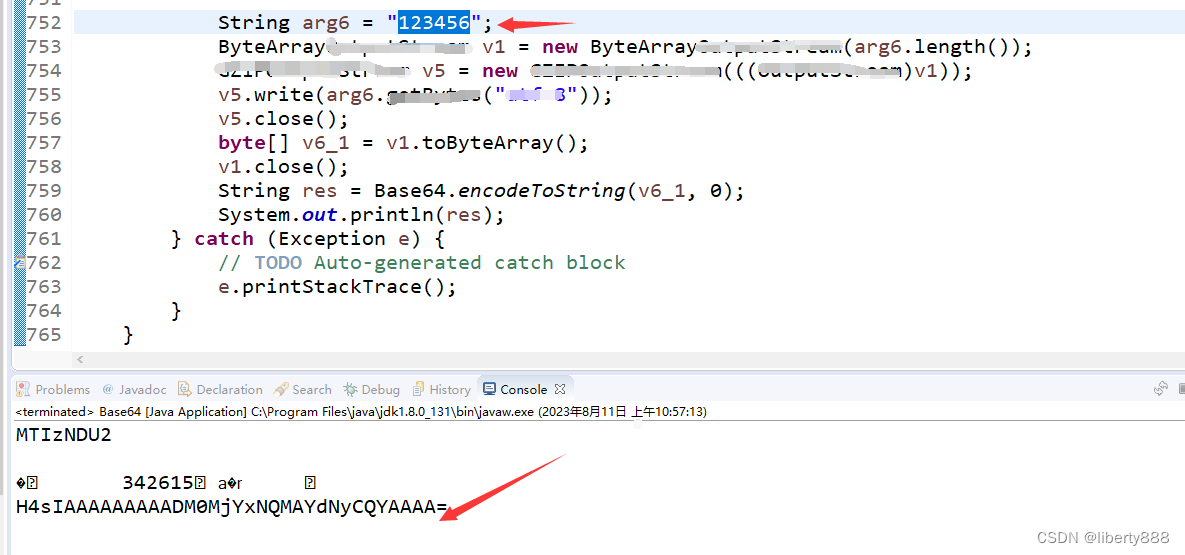
 这个123456加密结果就和APP一致了。APP结果可以hook输出看下。具体不难，自己练练手吧。

纯技术交流，请勿用于非法用途,如有权益问题可以发私信联系我删除.

付费课程：对于爬虫、逆向、抓包、接口构造感兴趣的同学可以了解下
猫敷雪
04-27 2766
因人而异，感兴趣的同学可以私聊我，进行针对性指导、教学。线上或者线下课程皆可，一对一教学。
h5st4.8参数逆向分析与算法还原
吴秋霖的博客
06-02 4438
最新h5st（4.8）参数分析与纯算法还原
某麦网抢票工具开发
qq_64428978的博客
08-02 4017
针对大麦网部分演唱会门票仅能在app渠道抢票的问题，研究了抢票接口并编写了抢票工具。
大麦网抢票程序（一）之大麦网网站分析
石璞东
12-18 1万+
大家好，我是石璞东。 今年元旦，我要和王璐瑶去北京看德云社的演出，所以需要购买两张德云社小园子的门票，按照网上的说法，官方渠道只有大麦网一家，而且元旦期间黄牛抢票肯定异常激烈，对于我这么一个又穷、手速又慢（顺便@一下研究生院，咳咳咳，奖学金和助学金该发了哈，交表那么积极，就是不给钱）的人来说，只能握住最后一根救命稻草了，那就是代码咯～ 对的，你没看错，我们这次不去凑12306的热闹了，我们来搞一下大麦网。 工欲善其事，必先利其器，要实现某个网站抢票过程的自动化，我们必须对目标网站有足够清晰的了解，请看分析。
大麦&逆向so
最新发布
m56423884698的博客
06-28 1381
大麦抢票
演唱会门票的DM 最新x-sign、x-sgext、x-mini-wua、x-umt的加密算法
qq_44130722的博客
05-15 4172
x-sign、x-sgext、x-mini-wua、x-umt
大麦APP解密/B站麒麟逆向
TGwuge的博客
06-05 1149
【代码】大麦APP解密/B站麒麟逆向。
1688 sign参数加密分析
08-17
"sign"参数通常用于验证API请求的来源和完整性，它是通过将特定的组成部分（如token、时间戳、g以及请求参数）与一个预定义的密钥结合，然后经过加密算法处理得到的。这样的设计能够防止中间人攻击，因为任何篡改...
得物sign参数逆向分析与Python算法还原
吴秋霖的博客
04-20 4143
使用Python获取得物商品数据、包含Sign签名算法分析与Python算法还原
对称加密算法及其在网页逆向分析中的应用
ylfhpy的博客
03-15 1077
对称加密算法是一种加密和解密使用相同密钥的加密技术。在数据传输过程中，发送方首先使用预先约定好的密钥对明文进行加密操作，将其转换为密文。密文在网络中传输，即使被第三方截获，由于没有正确的密钥，也无法解读其中的内容。接收方在接收到密文后，使用相同的密钥对其进行解密，从而恢复出原始的明文。这种加密方式的优点在于加密和解密的速度快，能够高效地处理大量数据，适用于对性能要求较高的场景。
如何用Frida实现App爬虫的运行时Hook调试？.pdf
04-20
文档支持目录章节跳转同时还支持阅读器左侧大纲显示和章节快速定位，文档内容完整、条理清晰。文档内所有文字、图表、函数、目录等元素均显示正常，无任何异常情况，敬请您放心查阅与使用。文档仅供学习参考，请勿用作商业用途。 想轻松敲开编程大门吗？Python 就是你的不二之选！它作为当今最热门的编程语言，以简洁优雅的语法和强大的功能，深受全球开发者喜爱。该文档为你开启一段精彩的 Python 学习之旅。从基础语法的细致讲解，到实用项目的实战演练，逐步提升你的编程能力。无论是数据科学领域的数据分析与可视化，还是 Web 开发中的网站搭建，Python 都能游刃有余。无论你是编程小白，还是想进阶的老手，这篇博文都能让你收获满满，快一起踏上 Python 编程的奇妙之旅！
大麦抢票辅助（只抢待开抢中的）
04-27
大麦抢票辅助（只抢待开抢中的） 重要提示：因为该软件原理是抓取页面ui控件id，模拟点击 如果页面渲染太慢，就会抓取失败导致点击超时无效，所以可以手动辅助点击 该软件只能起到辅助效果，帮忙快速点击 推荐：不能稳定打开跳转到抢票页的话，可以开启软件后，手动将大麦挂在抢票页 注意：一定要提前选好场次、价格还有观影人，收藏到想看 操作步骤 先去演唱会主页预选好场次、价格还有观演人，点击想看 （可选）手机后台杀掉大麦app任务 打开辅助app，给于对应权限 （可选）输入歌手名字，默认五月天 点击开抢按钮即可 如果点击开抢后，页面未开始自动跳转，可手动杀死大麦，再次切到辅助app点击开抢 如果想终止辅助app，点击右上角悬浮窗<点击停止>即可
webpack实战：某网站RSA登录加密逆向分析
吴秋霖的博客
09-12 8828
某网站登录RSA加密，深度分析webpack代码并构建完整的加密webpack代码！
【Python脚本】Python自动大麦网抢票，准点原价秒杀演唱会门票，拒绝黄牛交易！从我做起！！！1
热门推荐
weixin_45841831的博客
06-21 5万+
你是否错过了周杰伦的票，最近又没抢到五月天的票，不要太难过，今晚有张学友的票，后天还有张杰的票，加油哦！
关于大麦网接口抢票构造的一些思路
猫敷雪
10-31 8738
之前写的基于selenium版本的大麦网抢票思路，比较依赖页面元素，如果网页元素经常发生变动，代码需要随之改动，并且随着后期验证码的出现，将抢购流程提高了一个难度，虽然基于selenium版本已经实现了对于滑块的处理，但终究不甚满意。关于上述提到的内容，可以参考如下文章进行复现。大麦支持选座位、定时等功能大麦网滑块验证码自动识别针对自动识别大麦网滑块验证码，提出解决方案，并进行分析、总结。
1.安卓逆向-说明
计算机王的博客
09-11 1270
安卓逆向 安卓协议分析 app协议分析 保姆级攻略 app逆向 Android apk逆向
淘宝x-sign算法demo示例
m0_71316877的博客
06-16 1430
用xposed hook这个方法就可以拿到对应的签名，需要可以留言
大麦网技术二三事
weixin_40760343的博客
10-24 7985
杭州周杰伦2017年项目，大麦网抢票系统抢瘫了，据传阿里内部炸了锅，大麦在阿里序列里直接进入了被鄙视链的第一名，江湖上也是声名狼藉。作为大麦故人，我已经是不止一次的在各种场合听到诸如“大麦网技术水平太烂了”、“大麦基本没什么技术含量”、“大麦的技术还处于旧石器时代”等评论。对于差评，系统宕机摆在眼前，也确实是无需辩驳；但作为大麦网初创团队成员与最有资格谈论大麦技术的成员之一，犹豫再三，还是决定聊一
ECC加密算法具体运算
02-19
### ECC 加密算法的具体运算过程 #### 1. 参数选择 为了实施 ECC 加密，首先需要选定一条定义于特定有限域上的椭圆曲线以及该曲线上的一点作为基点 \( G \)[^1]。 对于实际应用而言，通常会选择如下参数： - **\( p \)**：一个大质数，用于指定有限域 GF(p)，即所有操作都在模 \( p \) 的情况下执行。 - **a, b**：两个系数，用来描述椭圆曲线方程的形式 \( y^2 = x^3 + ax + b \mod p \)。 - **G (Base Point)**：位于所选椭圆曲线上的已知点，也称为生成元。 - **n**：子群阶数，表示从基点出发通过加法能够到达的最大不同点的数量；它是一个非常大的整数。 这些参数共同构成了公开的系统参数集合，在整个通信过程中保持不变并被双方知晓[^2]。 #### 2. 密钥对生成 私钥 \( d_A \) 是一个小于 n 的随机正整数。对应的公钥 \( Q_A \) 则由下述方式计算得出: \[Q_A=d_AG\] 这里 \( Q_A \) 表示用户的公钥，而 \( d_A \) 即为其私钥。此步骤利用了椭圆曲线上的标量乘法特性——给定两点很容易求得它们相加的结果，但如果只知道其中一个点及其倍数，则很难反推出另一个原始点的位置关系[^3]。 #### 3. 数据加密流程 假设发送者想要向接收者传递消息 M ，则按照以下步骤完成加密处理： - 发送者选取临时私钥 k 并据此算出相应的公共组件 K=kG； - 计算共享秘密 S=[d_B]K 或等价形式 S=[k]Q_B （其中 B 方持有私钥 d_B 及其对应公钥 Q_B），这一步骤依赖于双方面预先协商好的对方公钥信息； - 将明文转换成适合编码到椭圆曲线上的格式 Pm； - 使用上述得到的秘密值S 对Pm 进行某种掩蔽变换 C=Pm+S*G 得到最终的密文C； - 同时附带传输额外的信息如 K 给接收端以便解码验证。 ```python def ecc_encrypt(public_key_QB, message_point_Pm): import random # 假设已经选择了合适的椭圆曲线参数和基点G curve_params = {'p': ..., 'a': ..., 'b': ...} base_point_G = ... # 随机选择临时私钥k temp_private_key_k = random.randint(1, n-1) # 计算公共组件K=kG public_component_K = scalar_multiply(temp_private_key_k, base_point_G) # 获取接收者的公钥QB receiver_public_key_QB = public_key_QB # 计算共享秘密S=[k]QB shared_secret_S = scalar_multiply(temp_private_key_k, receiver_public_key_QB) # 应用共享秘密对消息进行掩蔽变换获得密文C ciphertext_C = add_points(message_point_Pm, multiply_point(shared_secret_S, base_point_G)) return (public_component_K, ciphertext_C) # 辅助函数: 实现椭圆曲线上点的加法、倍增及标量乘法 def add_points(P, Q): ... def double_point(P): ... def scalar_multiply(k, P): ... ``` #### 4. 解密过程 当接收到包含有附加信息 K 和密文 C 的数据包后，接收方可依据自身持有的私钥 \( d_B \) 来恢复原消息： - 接收者先重新构建相同的共享秘密 S'=[d_B]K； - 然后再逆向移除之前施加过的掩蔽效果从而还原初始的消息点位置 Pm'=C-S'*G； - 最终将所得坐标映射回原来的消息空间内读取出真正的内容M。 ```python def ecc_decrypt(private_key_dB, received_data): public_component_K, ciphertext_C = received_data # 根据自己的私钥dB重建共享秘密S' reconstructed_shared_secret_S_prime = scalar_multiply(private_key_dB, public_component_K) # 移除掩蔽获取原文本点Pm' original_message_point_Pm_prime = subtract_points(ciphertext_C, multiply_point(reconstructed_shared_secret_S_prime, base_point_G)) # 映射回消息空间内的真实内容M decrypted_message_M = map_to_original_space(original_message_point_Pm_prime) return decrypted_message_M # 辅助函数: 完成减法操作和其他必要的映射工作 def subtract_points(C, masked_value): ... def map_to_original_space(point_on_curve): ... ```
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

liberty888

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值