1. 区间动态规划简介
1.1 区间动态规划定义
区间动态规划:线性 DP 的一种,简称为「区间 DP」。以「区间长度」划分阶段,以两个坐标(区间的左、右端点)作为状态的维度。一个状态通常由被它包含且比它更小的区间状态转移而来。
区间 DP 的主要思想就是:先在小区间内得到最优解,再利用小区间的最优解合并,从而得到大区间的最优解,最终得到整个区间的最优解。
根据小区间向大区间转移情况的不同,常见的区间 DP 问题可以分为两种:
-
单个区间从中间向两侧更大区间转移的区间 DP 问题。比如从区间 [i + 1, j - 1] 转移到更大区间 [i, j]。
-
多个(大于等于 2 个)小区间转移到大区间的区间 DP 问题。比如从区间 [i, k] 和区间 [k, j] 转移到区间 [i, j]。
下面我们讲解一下这两种区间 DP 问题的基本解题思路。
1.2 区间 DP 问题的基本思路
1.2.1 第 1 种区间 DP 问题基本思路
从中间向两侧转移的区间 DP 问题的状态转移方程一般为:dpi = max \lbrace dpi + 1, \quad dpi + 1, \quad dpi \rbrace + costi, \quad i \le j。
-
其中 dpi 表示为:区间 [i, j](即下标位置 i 到下标位置 j 上所有元素)上的最大价值。
-
cost 表示为:从小区间转移到区间 [i, j] 的代价。
-
这里的 max / min 取决于题目是求最大值还是求最小值。
从中间向两侧转移的区间 DP 问题的基本解题思路如下:
-
枚举区间的起点;
-
枚举区间的终点;
-
根据状态转移方程计算从小区间转移到更大区间后的最优值。
对应代码如下:
-
for i
in
range(size -
1, -
1, -
1):
# 枚举区间起点
-
for j
in
range(i +
1, size):
# 枚举区间终点
-
# 状态转移方程,计算转移到更大区间后的最优值
-
dp[i][j] =
max(dp[i +
1][j -
1], dp[i +
1][j], dp[i][j -
1]) + cost[i][j]
1.2.3 第 2 种区间 DP 问题基本思路
多个(大于等于 2 个)小区间转移到大区间的区间 DP 问题的状态转移方程一般为:dpi = max / min \lbrace dpi + dpk + 1 + costi \rbrace,\quad i < k \le j。
-
其中状态 dpi 表示为:区间 [i, j] (即下标位置 i 到下标位置 j 上所有元素)上的最大价值。
-
costi 表示为:将两个区间 [i, k] 与 [k + 1, j] 中的元素合并为区间 [i, j] 中的元素的代价。
-
这里的 max / min 取决于题目是求最大值还是求最小值。
多个小区间转移到大区间的区间 DP 问题的基本解题思路如下:
-
枚举区间长度;
-
枚举区间的起点,根据区间起点和区间长度得出区间终点;
-
枚举区间的分割点,根据状态转移方程计算合并区间后的最优值。
对应代码如下:
-
for l
in
range(
1, n):
# 枚举区间长度
-
for i
in
range(n):
# 枚举区间起点
-
j = i + l -
1
# 根据起点和长度得到终点
-
if j >= n:
-
break
-
dp[i][j] =
float(
'-inf')
# 初始化 dp[i][j]
-
for k
in
range(i, j +
1):
# 枚举区间分割点
-
# 状态转移方程,计算合并区间后的最优值
-
dp[i][j] =
max(dp[i][j], dp[i][k] + dp[k +
1][j] + cost[i][j])
2. 区间 DP 问题的应用
下面我们根据几个例子来讲解一下区间 DP 问题的具体解题思路。
2.1 最长回文子序列
2.1.1 题目链接
2.1.2 题目大意
描述:给定一个字符串 s。
要求:找出其中最长的回文子序列,并返回该序列的长度。
说明:
-
子序列:不改变剩余字符顺序的情况下,删除某些字符或者不删除任何字符形成的一个序列。
-
1 \le s.length \le 1000。
-
s 仅由小写英文字母组成。
示例:
-
示例 1:
输入:s = "bbbab" 输出:4 解释:一个可能的最长回文子序列为 "bbbb"。
-
示例 2:
输入:s = "cbbd" 输出:2 解释:一个可能的最长回文子序列为 "bb"。
2.1.3 解题思路
思路 1:动态规划
1. 划分阶段
按照区间长度进行阶段划分。
2. 定义状态
定义状态 dpi 表示为:字符串 s 在区间 [i, j] 范围内的最长回文子序列长度。
3. 状态转移方程
我们对区间 [i, j] 边界位置上的字符 s[i] 与 s[j] 进行分类讨论:
-
如果 s[i] = s[j],则 dpi 为区间 [i + 1, j - 1] 范围内最长回文子序列长度 + 2,即 dpi = dpi + 1 + 2。
-
如果 s[i] \ne s[j],则 dpi 取决于以下两种情况,取其最大的一种:
则状态转移方程为:
dpi = \begin{cases} max \lbrace dpi + 1 + 2 \rbrace & s[i] = s[j] \cr max \lbrace dpi, dpi - 1 \rbrace & s[i] \ne s[j] \end{cases}
4. 初始条件
-
单个字符的最长回文序列是 1,即 dpi = 1。
5. 最终结果
由于 dpi 依赖于 dpi + 1、dpi + 1、dpi,所以我们应该按照从下到上、从左到右的顺序进行遍历。
根据我们之前定义的状态,dpi 表示为:字符串 s 在区间 [i, j] 范围内的最长回文子序列长度。所以最终结果为 dp0。
思路 1:代码
-
class
Solution:
-
def
longestPalindromeSubseq(
self, s: str) ->
int:
-
size =
len(s)
-
dp = [[
0
for _
in
range(size)]
for _
in
range(size)]
-
for i
in
range(size):
-
dp[i][i] =
1
-
-
for i
in
range(size -
1, -
1, -
1):
-
for j
in
range(i +
1, size):
-
if s[i] == s[j]:
-
dp[i][j] = dp[i +
1][j -
1] +
2
-
else:
-
dp[i][j] =
max(dp[i +
1][j], dp[i][j -
1])
-
-
return dp[
0][size -
1]
思路 1:复杂度分析
-
时间复杂度:O(n^2),其中 n 为字符串 s 的长度。
-
空间复杂度:O(n^2)。
2.2 戳气球
2.2.1 题目链接
2.2.2 题目大意
描述:有 n 个气球,编号为 0 \sim n - 1,每个气球上都有一个数字,这些数字存在数组 nums 中。现在开始戳破气球。其中戳破第 i 个气球,可以获得 nums[i - 1] \times nums[i] \times nums[i + 1] 枚硬币,这里的 i - 1 和 i + 1 代表和 i 相邻的两个气球的编号。如果 i - 1 或 i + 1 超出了数组的边界,那么就当它是一个数字为 1 的气球。
要求:求出能获得硬币的最大数量。
说明:
-
n == nums.length。
-
1 \le n \le 300。
-
0 \le nums[i] \le 100。
示例:
-
示例 1:
输入:nums = [3,1,5,8] 输出:167 解释: nums = [3,1,5,8] --> [3,5,8] --> [3,8] --> [8] --> [] coins = 3*1*5 + 3*5*8 + 1*3*8 + 1*8*1 = 167
-
示例 2:
输入:nums = [1,5] 输出:10 解释: nums = [1,5] --> [5] --> [] coins = 1*1*5 + 1*5*1 = 10
2.2.3 解题思路
思路 1:动态规划
根据题意,如果 i - 1 或 i + 1 超出了数组的边界,那么就当它是一个数字为 1 的气球。我们可以预先在 nums 的首尾位置,添加两个数字为 1 的虚拟气球,这样变成了 n + 2 个气球,气球对应编号也变为了 0 \sim n + 1。
对应问题也变成了:给定 n + 2 个气球,每个气球上有 1 个数字,代表气球上的硬币数量,当我们戳破气球 nums[i] 时,就能得到对应 nums[i - 1] \times nums[i] \times nums[i + 1] 枚硬币。现在要戳破 0 \sim n + 1 之间的所有气球(不包括编号 0 和编号 n + 1 的气球),请问最多能获得多少枚硬币?
1. 划分阶段
按照区间长度进行阶段划分。
2. 定义状态
定义状态 dpi 表示为:戳破所有气球 i 与气球 j 之间的气球(不包含气球 i 和 气球 j),所能获取的最多硬币数。
3. 状态转移方程
假设气球 i 与气球 j 之间最后一个被戳破的气球编号为 k。则 dpi 取决于由 k 作为分割点分割出的两个区间 (i, k) 与
(k, j) 上所能获取的最多硬币数 + 戳破气球 k 所能获得的硬币数,即状态转移方程为:
dpi = max \lbrace dpi + dpk + nums[i] \times nums[k] \times nums[j] \rbrace, \quad i < k < j
4. 初始条件
5. 最终结果
根据我们之前定义的状态,dpi 表示为:戳破所有气球 i 与气球 j 之间的气球(不包含气球 i 和 气球 j),所能获取的最多硬币数。所以最终结果为 dp0。
思路 1:代码
-
class
Solution:
-
def
maxCoins(
self, nums: List[int]) ->
int:
-
size =
len(nums)
-
arr = [
0
for _
in
range(size +
2)]
-
arr[
0] = arr[size +
1] =
1
-
for i
in
range(
1, size +
1):
-
arr[i] = nums[i -
1]
-
-
dp = [[
0
for _
in
range(size +
2)]
for _
in
range(size +
2)]
-
-
for l
in
range(
3, size +
3):
-
for i
in
range(
0, size +
2):
-
j = i + l -
1
-
if j >= size +
2:
-
break
-
for k
in
range(i +
1, j):
-
dp[i][j] =
max(dp[i][j], dp[i][k] + dp[k][j] + arr[i] * arr[j] * arr[k])
-
-
return dp[
0][size +
1]
思路 1:复杂度分析
-
时间复杂度:O(n^3),其中 n 为气球数量。
-
空间复杂度:O(n^2)。
2.3 切棍子的最小成本
2.3.1 题目链接
2.3.2 题目大意
描述:给定一个整数 n,代表一根长度为 n 个单位的木根,木棍从 0 \sim n 标记了若干位置。例如,长度为 6 的棍子可以标记如下:
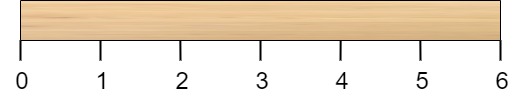
再给定一个整数数组 cuts,其中 cuts[i] 表示需要将棍子切开的位置。
我们可以按照顺序完成切割,也可以根据需要更改切割顺序。
每次切割的成本都是当前要切割的棍子的长度,切棍子的总成本是所有次切割成本的总和。对棍子进行切割将会把一根木棍分成两根较小的木棍(这两根小木棍的长度和就是切割前木棍的长度)。
要求:返回切棍子的最小总成本。
说明:
-
2 \le n \le 10^6。
-
1 \le cuts.length \le min(n - 1, 100)。
-
1 \le cuts[i] \le n - 1。
-
cuts 数组中的所有整数都互不相同。
示例:
-
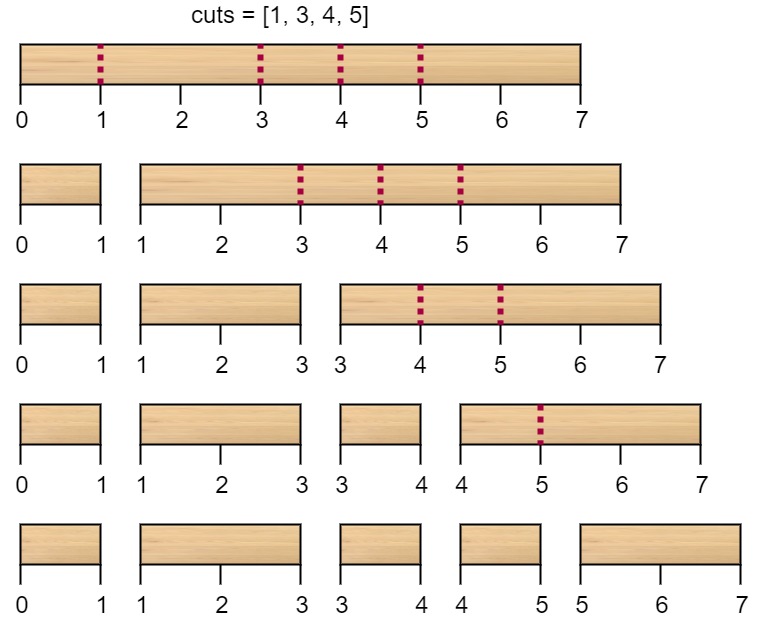
示例 1:
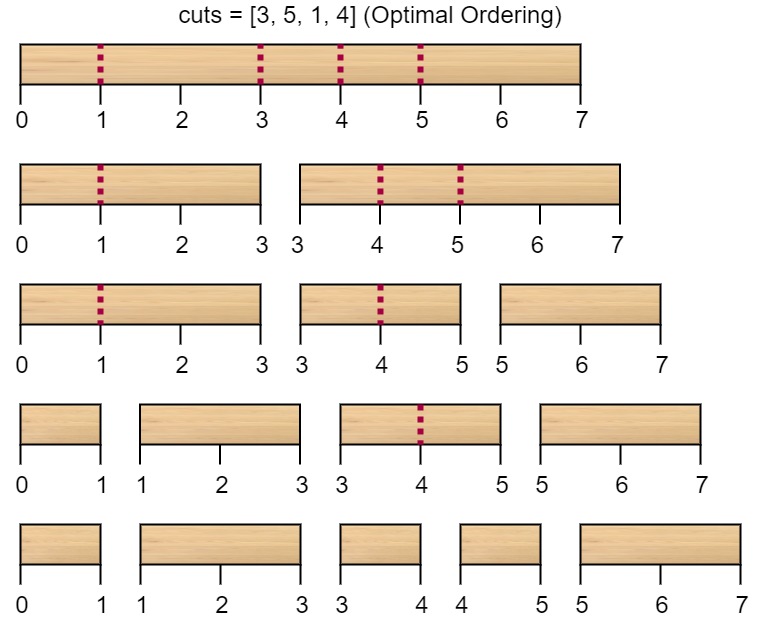
输入:n = 7, cuts = [1,3,4,5] 输出:16 解释:按 [1, 3, 4, 5] 的顺序切割的情况如下所示。 第一次切割长度为 7 的棍子,成本为 7 。第二次切割长度为 6 的棍子(即第一次切割得到的第二根棍子),第三次切割为长度 4 的棍子,最后切割长度为 3 的棍子。总成本为 7 + 6 + 4 + 3 = 20 。而将切割顺序重新排列为 [3, 5, 1, 4] 后,总成本 = 16(如示例图中 7 + 4 + 3 + 2 = 16)。
-
示例 2:
输入:n = 9, cuts = [5,6,1,4,2] 输出:22 解释:如果按给定的顺序切割,则总成本为 25。总成本 <= 25 的切割顺序很多,例如,[4, 6, 5, 2, 1] 的总成本 = 22,是所有可能方案中成本最小的。
2.3.3 解题思路
思路 1:动态规划
我们可以预先在数组 cuts 种添加位置 0 和位置 n,然后对数组 cuts 进行排序。这样待切割的木棍就对应了数组中连续元素构成的「区间」。
1. 划分阶段
按照区间长度进行阶段划分。
2. 定义状态
定义状态 dpi 表示为:切割区间为 [i, j] 上的小木棍的最小成本。
3. 状态转移方程
假设位置 i 与位置 j 之间最后一个切割的位置为 k,则 dpi 取决与由 k 作为切割点分割出的两个区间 [i, k] 与 [k, j] 上的最小成本 + 切割位置 k 所带来的成本。
而切割位置 k 所带来的成本是这段区间所代表的小木棍的长度,即 cuts[j] - cuts[i]。
则状态转移方程为:dpi = min \lbrace dpi + dpk + cuts[j] - cuts[i] \rbrace, \quad i < k < j
4. 初始条件
5. 最终结果
根据我们之前定义的状态,dpi 表示为:切割区间为 [i, j] 上的小木棍的最小成本。 所以最终结果为 dp0。
思路 1:代码
-
class
Solution:
-
def
minCost(
self, n: int, cuts: List[int]) ->
int:
-
cuts.append(
0)
-
cuts.append(n)
-
cuts.sort()
-
-
size =
len(cuts)
-
dp = [[
float(
'inf')
for _
in
range(size)]
for _
in
range(size)]
-
for i
in
range(
1, size):
-
dp[i -
1][i] =
0
-
-
for l
in
range(
3, size +
1):
# 枚举区间长度
-
for i
in
range(size):
# 枚举区间起点
-
j = i + l -
1
# 根据起点和长度得到终点
-
if j >= size:
-
continue
-
dp[i][j] =
float(
'inf')
-
for k
in
range(i +
1, j):
# 枚举区间分割点
-
# 状态转移方程,计算合并区间后的最优值
-
dp[i][j] =
min(dp[i][j], dp[i][k] + dp[k][j] + cuts[j] - cuts[i])
-
return dp[
0][size -
1]
思路 1:复杂度分析
-
时间复杂度:O(m^3),其中 m 为数组 cuts 的元素个数。
-
空间复杂度:O(m^2)。























 757
757











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








