数二-一元函数微分学

基础

$$\begin{gathered} \int x^{k}dx=\frac{1}{(k+1)}{x}^{(k+1)}+C \\ \int \frac{1}{x}dx=\ln |x|+C \\ \int e^{x}dx=e^x+C,\int a^{x}dx=\frac{1}{\ln a}{a}^x+C \\ \int \ln x=x\ln x+C \\ \int \sin xdx=-\cos x+C,\int \cos x=\sin x+C \\ \int \tan xdx=-\ln |\cos x|+C,\int \cot x=\ln |\sin x|+C \\ \int \sec xdx=\ln |\sec x+\tan x|+C \\ \int \csc xdx=\ln |\csc x-\cot x|+C \\ \int {\sec }^{2}xdx=\tan x+C,\int {\csc }^{2}xdx=-\cot x+C \\ \int \sec x\tan xdx=\sec x+C,\int \csc x\cot xdx=-\csc x+C \\ \int \frac{1}{1+x^2}dx=\arctan x+C,\int \frac{1}{a^2+x^2}dx=\frac{1}{a}\arctan \frac{x}{a}+C \\ \int \frac{1}{\sqrt{1-x^2}}dx=\arcsin x+C,\int \frac{1}{\sqrt{a^2-x^2}}dx=\arcsin \frac{x}{a}+C \\ \int \frac{1}{\sqrt{x^2+a^2}}dx=\ln (x+\sqrt{x^2+a^2})+C, \\ \int \frac{1}{\sqrt{x^2-a^2}}dx=\ln |x+\sqrt{x^2-a^2}|+C \\ \int \frac{1}{x^2-a^2}dx=\frac{1}{2a}\ln \left|\frac{x-a}{x+a}\right|+C,\int \frac{1}{a^2-x^2}dx=\frac{1}{2a}\ln \left|\frac{x+a}{x-a}\right|+C \\ \int \sqrt{a^2-x^2}dx=\frac{a^2}{2}\arcsin \frac{x}{a}+\frac{x}{2}\sqrt{a^2-x^2}+C \\ \int {\sin }^{2}xdx=\frac{1}{2}x-\frac{\sin 2x}{4}+C({\sin }^{2}x=\frac{1-\cos 2x}{2}) \\ \int {\cos }^{2}xdx=\frac{1}{2}x+\frac{\sin 2x}{4}+C({\cos }^{2}x=\frac{1+\cos 2x}{2}) \\ \int {\tan }^{2}xdx=\tan x-x+C({\tan }^{2}x={\sec }^2-1) \\ \int {\cot }^{2}xdx=-\cot x-x+C({\cot }^{2}x={\csc }^{2}x-1) \end{gathered}$$

一次三角函数分式配系数方法

$求\int \frac{\sin x-\cos x}{\sin x+2\cos x}dx$

$$\begin{gathered} 令\sin x-\cos x=a(\sin x+2\cos x)+b(\sin x+2\cos x{)}^{\prime } \\ 解得：a=-\frac{1}{5},b=-\frac{3}{5} \\ \therefore \begin{array}{rl}\int \frac{\sin x-\cos x}{\sin x+2\cos x}dx=& -\frac{1}{5}\int dx-\frac{3}{5}\int \frac{d(\sin x+2\cos x)}{\sin x+2\cos x}\\ =& -\frac{1}{5}-\frac{3}{5}\ln |\sin x+2\cos x|+C\end{array} \end{gathered}$$

华理士公式

$${\int }_0^{\frac{\pi }{2}}{\sin }^{n}x={\int }_0^{\frac{\pi }{2}}{\cos }^{n}x=\{\begin{array}{ll}\frac{n-1}{n}\ast \frac{n-3}{n-2}\ast \cdots \ast \frac{1}{2}\ast \frac{\pi }{2}& n为偶数\\ \frac{n-1}{n}\ast \frac{n-3}{n-2}\ast \cdots \ast \frac{2}{3}& n为奇数\end{array}$$

常见有原函数，但无初等函数形式的原函数

主要用于二重积分，积分次序的选择。

$\{\begin{array}{l}\int \frac{\sin x}{x}dx\int \frac{\cos x}{x}dx\int \frac{\tan x}{x}dx\\ \\ \int \frac{e^x}{x}dx\int \sin \frac{1}{x}dx\int \cos \frac{1}{x}dx\\ \\ \int e^{a{x}^2+bx+c}dx\int \frac{dx}{\ln x}\end{array}$

定积分

定积分精确定义

$${\int }_a^{b}f(x)dx=\underset{n\to \infty }{\lim }\sum _{i=1}^{n}f(a+\frac{b-a}{n}i)\frac{b-a}{n}$$
当a=0,b=1时
$${\int }_0^{1}f(x)dx=\underset{n\to \infty }{\lim }\sum _{i=1}^{n}f(\frac{i}{n})\frac{1}{n}$$

*定积分精确定义与夹逼定理综合应用

$求极限\underset{n\to \infty }{\lim }{\sum }_{i=1}^n\frac{\sin \frac{i\pi }{n}}{n+\frac{1}{i}}$

$f(x)=\frac{\sin \frac{i\pi }{n}}{n}\ast \frac{n}{n+1}=\frac{\sin \frac{i\pi }{n}}{n+1}\le \frac{\sin \frac{i\pi }{n}}{n+\frac{1}{i}}\le \frac{\sin \frac{i\pi }{n}}{n}=g(x)$

${\int }_0^{1}f(x)dx={\int }_0^1\sin \pi xdx=\frac{2}{\pi }$
同理:${\int }_0^{1}g(x)dx=\frac{2}{\pi }$
有夹逼定理得:
$\underset{n\to \infty }{\lim }{\sum }_{i=1}^n\frac{\sin \frac{i\pi }{n}}{n+\frac{1}{i}}=\frac{2}{\pi }$

定积分存在定理

1. $若f(x)在[a,b]上连续,则{\int }_a^{b}f(x)dx存在.$
2. $若f(x)在[a,b]上单调,则{\int }_a^{b}f(x)dx存在.$
3. $若f(x)在[a,b]上有界，且只有有限个间断点，则{\int }_a^{b}f(x)dx存在.$

原函数（不定积分）存在定理

1. $连续函数f(x)必有原函数.$
2. $含有第一类间断点、无穷间断点的函数f(x)在包含间断点的区间必没有原函数F(x).$

定积分计算（牛顿-莱布尼兹公式）

$${\int }_a^{b}f(x)dx\stackrel{F^{\prime }(x)=f(x)}{=}F(b)-F(a)$$

分部积分法

${\int }_a^{b}u(x)v^{\prime }(x)dx=u(x)v(x){|}_a^b-{\int }_a^{b}v(x)u^{\prime }(x)dx$

建议看张宇图标法，在多次分部积分上，相对更直观，这里不再过多赘述。
相关视频笔者已经上传公众号“翼点通”，回复张宇即可。

$\Gamma$函数

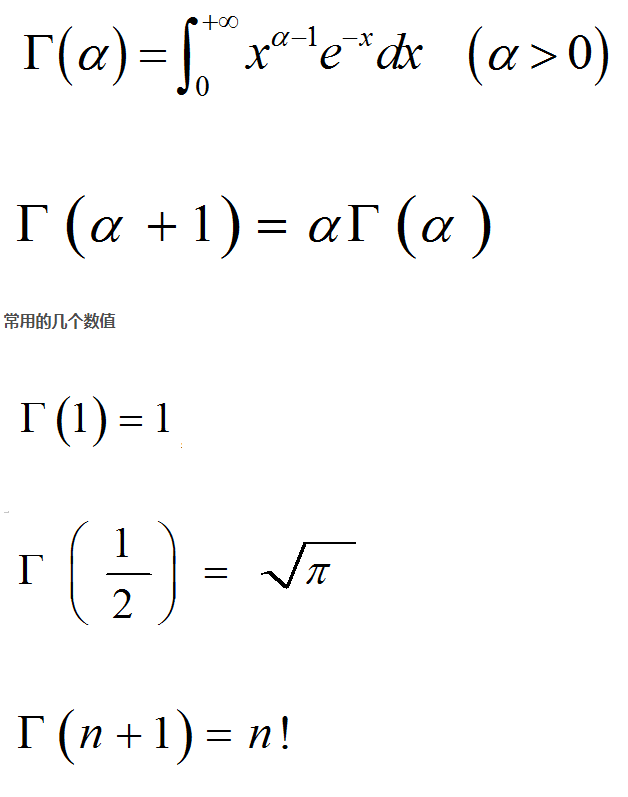
变限积分

变限积分求导公式

$[{\int }_{g(x)}^{h(x)}f(t)dt{]}^{\prime }=f[h(x)]h^{\prime }(x)-f[g(x)]g^{\prime }(x)$

平面图形面积

• $曲线y=y_1(x)和y=y_2(x)在x=a,到x=b所围成的面积$
  $$S={\int }_a^b|y_1(x)-y_2(x)|dx$$

• $曲线r=r_1(\vartheta )和r=r_2(\vartheta )在射线\vartheta =\alpha ,\vartheta =\beta 所围成的扇形面积$
  $$S=\frac{1}{2}{\int }_{\alpha }^{\beta }|r_1^2(\vartheta )-r_2^2(\vartheta )|d\vartheta$$

参数方程面积计算

$\{\begin{array}{l}x=x(t)\\ y=y(t)\end{array}f(x)=\frac{y(t)}{x(t)}$
$\begin{array}{rl}S& ={\int }_{\alpha }^{\beta }f(x)dx\\ & ={\int }_{t(\alpha )}^{t(\beta )}y(t)x^{\prime }(t)dt\end{array}$

函数面积与旋转体体积

$$S={\int }_a^{b}y(x)dx$$
$$V_x={\int }_a^b\pi y^2(x)dx$$
$$V_y={\int }_a^{b}2\pi xy(x)dx$$

应用

曲率与曲率半径

变力沿直线做功

*抽水做功

水压力

形心坐标

弧长

旋转曲面的表面积

平行截面面积已知的立体体积

例