【数学精讲】π

        是用来干什么的呢？有什么用？想必没到六年级的孩子大多都会有这个疑问。现在我给你们讲解一下吧；

       是指在同一圆中周长和直径的比值。所以，或者说

        根据C和d的关系，我们可以知道圆周长的计算公式是：或

        这时候会有同学有疑问了：圆的面积怎么求呢？

        别急，我来给你讲一下吧。

        

        上图是圆面积推导过程，如图，将一个圆平均分为16份，将这十六份如上所示摆成一个近似的长方形，由于长方形的面积公式是而,,所以圆面积计算公式是：。

        这时候有同学会问了：那拼成的近似长方形的长是凹凸不平的，怎么能计算面积呢？

        其实想一想，将圆平均分为份之后，每一份是不是变成了一条线呢。将每条线排列好后，圆就可以变成长方形了。

        其实圆的面积公式还有别的推导方法，如：微积分  .三角函数......

        这里就列举微积分的解法：

                【扇形面积累加】：

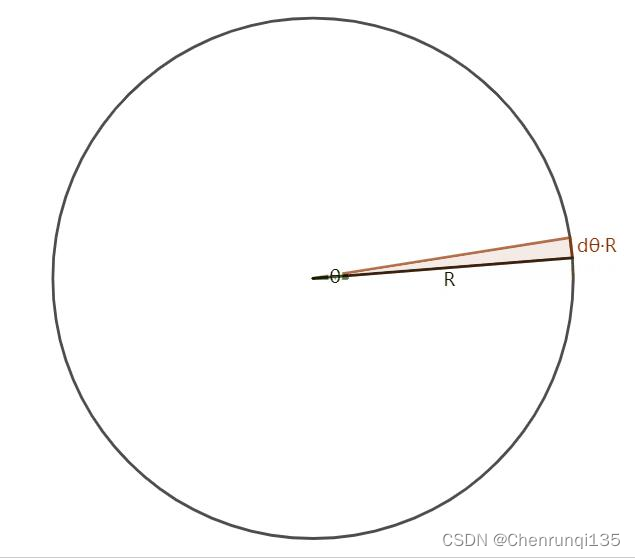
如上图，假定圆的半径为R，设θ 为[0, 2π]之间的角度（弧度制）。那么整个圆可以看成由无数个始边角度为θ，终边角度为θ+dθ扇形所组成，而圆的面积也就是这无数个扇形面积的累加。由于扇形的夹角（dθ）极其微小，其所对应的弧近乎直线，因而可将其看成极其尖细的等腰三角形——其底边=弧长，高=半径。根据弧度的定义 

 ，可知dθ所对应的弧长就等于 dθ·R，三角形的面积就= 

，而圆的面积也就是。

        接下来，我来讲解一下如何求出。

       

求π的公式有很多种，其中最著名的是莱布尼茨级数和马青公式。以下是这两个公式的介绍：

1. 莱布尼茨级数： 莱布尼茨级数是一种用于计算π的无穷级数。它的公式如下：这个级数是一个交替级数，通过不断增加级数的项，可以逐渐逼近π/4的值。当级数的项数越多时，逼近的精度也会越高。

2. 马青公式： 马青公式是一种用于计算π的无穷乘积公式。它的公式如下： 这个公式中的每一项都是两个连续的整数相除，通过不断增加乘积的项，可以逐渐逼近π/2的值。同样地，当乘积的项数越多时，逼近的精度也会越高。            谢谢观看