基于贝叶斯定理的病情诊断案例分析

---

案例背景

已知一个患者感染了一种罕见的疾病，现医生想通过后验概率的信息来诊断患者感染的疾病类型。

建立一个关于疾病类型和疾病症状的贝叶斯网络，用二元随机变量 D ∈ { 0 , 1 } D\in\{0,1\} D∈{0,1} 表示这种疾病的两种类型，用二元随机变量 S k ∈ { 0 , 1 } , k = 1 , 2 , . . . , n S_k\in\{0,1\}, k=1,2,...,n Sk​∈{0,1},k=1,2,...,n 表示是否检测到第 $k$ 种症状，得到的贝叶斯网络如下（节点表示随机变量，边表示随机事件之间的概率关系）：

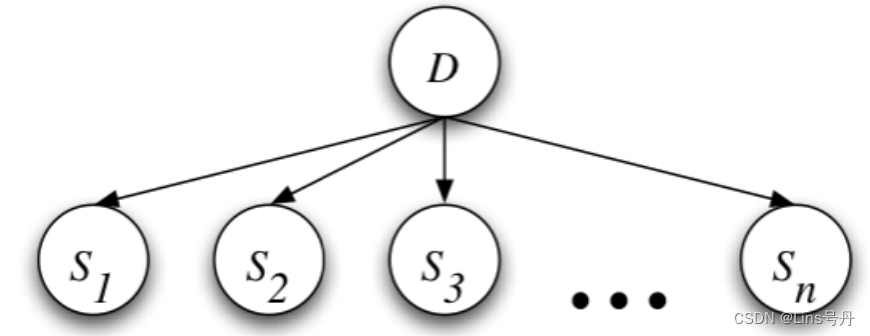
在没有可靠证据条件下，假定该疾病的两种类型都有可能发生，且发生概率相同，即：

$$P(D=0)=P(D=1)=\frac{1}{2}$$

当疾病类型 $D=0$ 时，所有的症状 k ∈ { 1 , 2 , . . . n } k\in\{1,2,...n\} k∈{1,2,...n} 均有可能被观察到，且每种症状被观察到的概率为 $1/2$，即：

P ( S k = 0 ∣ D = 0 ) = P ( S k = 1 ∣ D = 0 ) = 1 2 , ∀ k ∈ { 1 , 2 , . . . , n } P(S_k=0|D=0)=P(S_k=1|D=0)=\frac{1}{2},\forall k\in\{1,2,...,n\} P(Sk​=0∣D=0)=P(Sk​=1∣D=0)=21​,∀k∈{1,2,...,n}

当疾病类型 $D=1$ 时，则必定伴随着症状 $k=1$ 被观察到，即：$P(S_1=1|D=1)=1$，而症状 $k\ge 2$ 为阳性的概率公式为：

$$P(S_k=1|D=1)=\frac{f(k-1)}{f(k)}$$

其中，$f(k)=2^k+(-1{)}^k$。

病情诊断

如上案例背景提到的信息，我们知道在某种类型疾病发生后，观测到各种疾病症状的概率（用频率代替概率），但现在，医生希望根据积累观测到的症状，来判断患者感染的疾病类型，就需要用贝叶斯公式进行处理判读。

现在医生在某个月进行症状观测，在第 $k$ 天时检测症状 $k$，假设现在观测了 $m$ 天，均观测到症状 S k = 1 , k ∈ { 1 , 2 , . . . m } S_k=1,k\in \{1,2,...m\} Sk​=1,k∈{1,2,...m}，即积累的观测数据为 { S 1 = 1 , S 2 = 1 , . . . , S m = 1 } \{ S_1=1,S_2=1,...,S_m=1 \} {S1​=1,S2​=1,...,Sm​=1}，基于这些积累的观测数据，医生计算如下的比率来进行诊断：

$$r_m=\frac{P(D=0|S_1=1,S_2=1,...,S_m=1)}{P(D=1|S_1=1,S_2=2,...,S_m=1)}$$

如果该比率值大于1，则医生认为在当前观测到的症状表现下，诊断患者感染的疾病类型 $D=0$ 的准确性更高，反之则疾病类型更有可能为 $D=1$。

基于贝叶斯定理的诊断分析

贝叶斯定理利用对事件 B 的观察来更新对事件 A 发生概率的判断，通过先验概率和新观测的数据结合起来得到后验概率。在这里，我们知道疾病类型到疾病症状的概率，因此可以通过观测到的症状数据，来反过来推这些观测到的症状对应到疾病类型的概率。

$$P(A|B)=\frac{P(B|A)P(A)}{P(B)}$$

根据上述的 $r_m$ 公式，可知，$r_m$ 与 $m$ 之间存在直接关系（上述仅作为举例，不一定要求观测的症状都为阳性，只需要记录到 $m$ 个观测值）。那么 $r_m$ 与 $m$ 之间的公式如何？如果每次观测到的症状都为阳性，那医生是否能直接依赖于观测的天数进行诊断？

根据 $r_m$ 的公式，通过贝叶斯定理可得：

$$\begin{gathered} r_m=\frac{P(D=0|S_1=1,S_2=1,...,S_m=1)}{P(D=1|S_1=1,S_2=2,...,S_m=1)} \\ =\frac{P(S_1=1,S_2=1,...,S_m=1|D=0)P(D=0)/P(S_1=1,S_2=1,...,S_m=1)}{P(S_1=1,S_2=2,...,S_m=1|D=1)P(D=1)/P(S_1=1,S_2=1,...,S_m=1)} \\ =\frac{P(S_1=1,S_2=1,...,S_m=1|D=0)P(D=0)}{P(S_1=1,S_2=2,...,S_m=1|D=1)P(D=1)} \end{gathered}$$

通过全概率公式将事件拆开得：

$$r_m=\frac{P(S_1=1|D=0)P(S_2=1|D=0),...,P(S_m=1|D=0)P(D=0)}{P(S_1=1|D=1)P(S_2=1|D=1),...,P(S_m=1|D=1)P(D=1)}$$

根据前面得先验概率可知， P ( S k = 1 ∣ D = 0 ) = 1 / 2 ， ∀ k ∈ { 1 , 2 , . . . m } P(S_k=1|D=0)=1/2，\forall k\in\{1,2,...m\} P(Sk​=1∣D=0)=1/2，∀k∈{1,2,...m}，而疾病类型 $D=1$ 时症状 $k=1$ 必定为阳性，有 $P(S_1=1|D=1)=1$，其余症状 $k\ge 2$ 有：

$$P(S_k=1|D=1)=\frac{f(k-1)}{f(k)}$$

进一步地，根据 $P(D=0)=P(D=1)=1/2$，代入 $r_m$ 表达式可得：

$$r_m=\frac{(0.5{)}^m}{f(1)/f(m)}=f(m)(0.5{)}^m/f(1)=0.5^m\times [2^m+(-1{)}^m]$$

将该公式画图后可知，随着观测时长越长，$r_m$ 的值趋向于等于 1，在症状 $k=1$ 为阳性时更倾向于诊断为疾病类型 $D=1$。

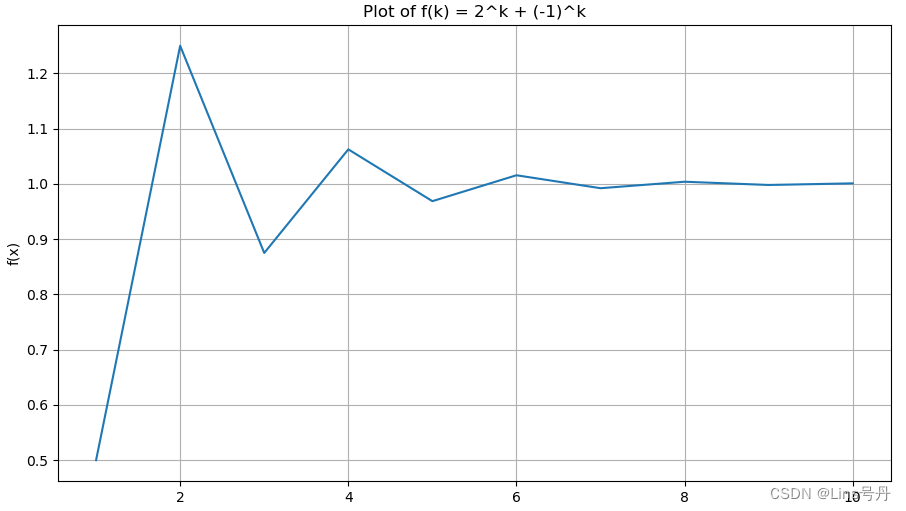
当检测到症状越来越多，即观测时长拉长，比率值更倾向于等于1，在这个过程中，医生给出的诊断是否逐渐变得确定可靠。