文章目录
本文章启发于 南军Opt 的相关文章,模型引自 Guy Desaulniers 等人的《Column Generation》,具体将会对已有模型和程序进行详细介绍和扩展。
1. 问题定义
前面我们介绍了带容量限制的车辆路径问题(Capacitated vehicle routing problem, CVRP),在CVRP的基础上,限制车辆到达各个客户点的时间范围,即客户点的时间窗,它限制了车辆到达该客户点的最早和最晚时间,称为带时间窗的车辆路径问题(Vehicle routing with time windows, VRPTW),该时间维度上的约束条件使得车辆的运输方案要考虑在途时间和到达时间之间的关系,极大地增加了模型的复杂性,该约束是VRP问题的典型约束。
处理时间窗的方式很简单,但都需要定义车辆到达客户点的时间变量,通过约束该时间变量的范围,实现时间窗约束,而车辆到达每个客户点的时间具有相互依赖关系,在同一车辆路线上的前后节点的到达时间相距时间不小于节点间的转运时间。时间窗约束的常见分类有两种:
- 硬时间窗:即车辆到达客户点的时间必须在指定的时间窗内,提前到达则在客户点处等待,而晚于时间窗到达则不被允许(方案不可行);
- 软时间窗:即车辆到达客户点的时间应尽量在指定时间窗范围内,如果不在指定时间窗范围内则会进行一定的惩罚,一般而言,晚于时间窗到达会有一个较大的惩罚系数,而早于时间窗到达是否惩罚则需要进行一定的声明。
2. VRPTW 数学模型
VRPTW 模型常常建立为多商品网络流模型(multi-commodity network flow model)的形式 ,在一定目标下考虑商品流量在网络结构中的流动。具体到 VRPTW 问题的数学模型,则引用参考教材《Column Generation》的第三章节,其中的时间窗约束为硬约束。
2.1 决策变量
根据 VRPTW 问题的描述可知,我们需要直接决策的变量是派哪一辆车去配送哪一段的路线,而间接决策的变量则是车辆到达某个客户点的到达时间,需要限制在一定范围内。变量以及参数如下:
- 模型决策变量:
- x i j k x_{ijk} xijk 布尔变量,车辆 k ∈ V k\in V k∈V 是否负责节点 i ∈ N i\in{N} i∈N 和节点 j ∈ N j\in N j∈N 之间的直接配送,若是则取值为 1 1 1,否则取值为 0 0 0;
- s i k s_{ik} sik 连续型变量,表示车辆 k ∈ V k\in V k∈V 到达节点 i ∈ N i\in N i∈N 的时间。
- 模型参数:
- c i j c_{ij} cij 表示节点 i ∈ N i\in N i∈N 到节点 j ∈ N j\in N j∈N 的权重(距离或是运输成本);
- d i d_i di 表示客户点 i ∈ C i\in C i∈C 的需求量;
- q q q 表示车辆的最大载重量(本模型默认车辆都是同质车辆);
- a i , b i a_i,b_i ai,bi 表示车辆到达客户点所必须的时间窗范围;
- t i j t_{ij} tij 表示从节点 i i i 到节点 j j j 之间的运输时间。
上面提到的集合 V V V 表示同质车辆的集合; N N N 表示所有节点的集合,包括起始节点 0 0 0 和客户节点 C C C,以及虚拟的返回节点 n + 1 n+1 n+1。
2.2 约束条件
约束条件是规定一个可行方案所必须满足的要求,由于我们基于的求解器 pyscipopt 是线性规划求解器,因此对于广义约束(如逻辑约束)需要进行线性化。值得注意的是,在 TSP 问题当中,有子环路消除的相关约束,而在 VRPTW 问题当中,较少听说需要额外地进行子环路消除,这是由于时间窗约束的形式是 MTZ 约束的形式,且节点间转运时间大于 0 0 0,因此时间窗约束默认已经消除了子环路,同理,在 CVRP 当中的运载量变化约束(车辆在各个客户点处的运载量都不超过最大载重)也起到相同的作用。
(1)流平衡约束
该约束是限制每个客户点只被访问 1 1 1 次,注意决策变量下标的范围,具体如下:
∑ k ∈ V ∑ j ∈ N \ 0 x i j k = ∑ k ∈ V ∑ j ∈ N \ { n + 1 } x j i k = 1 ∀ i ∈ C \sum_{k \in \mathcal{V}} \sum_{j \in \mathcal{N}\backslash 0} x_{i j k}=\sum_{k \in \mathcal{V}} \sum_{j \in \mathcal{N}\backslash \{n+1\}} x_{jik}=1 \quad \forall i \in \mathcal{C} k∈V∑j∈N\0∑xijk=k∈V∑j∈N\{n+1}∑xjik=1∀i∈C
以及,如果车辆访问了某个客户点,则进出该客户点数为 1 1 1,反之则为 0 0 0,意思为如果车辆 k k k 服务了某客户点,则服务之后需要离开,统一为车辆的进出流平衡:
∑ i ∈ N x i h k − ∑ j ∈ N x h j k = 0 ∀ h ∈ C , ∀ k ∈ V \sum_{i \in \mathcal{N}} x_{i h k}-\sum_{j \in \mathcal{N}} x_{h j k}=0 \quad \forall h \in \mathcal{C}, \quad \forall k \in \mathcal{V} i∈N∑xihk−j∈N∑xhjk=0∀h∈C,∀k∈V
(2)启用车辆全部返回
有两种解决车辆启用和回收约束的思路:
- 已知待启用的车辆数,此时在启用车辆集合当中的所有车辆,都需要从起始点出发,并最终返回到起始点(虚拟返回点),特别的,如果待启用的车辆并不都被使用,但为了保证车辆发出量和回收量的平衡,会让这些实际没有使用到的车辆从节点 0 0 0 直接到节点 n + 1 n+1 n+1;
- 另一种是不知道会启用多少的车辆数,只要求发出的车辆全都返回,且发出的车辆数要小于总的可派遣车辆数即可,本文采用此种约束思想。
∑ k ∈ V ∑ j ∈ N x 0 j k = ∑ k ∈ V ∑ i ∈ N x i , n + 1 , k ≤ ∣ V ∣ \sum_{k\in \mathcal{V}}\sum_{j \in \mathcal{N}} x_{0 j k}=\sum_{k\in\mathcal{V}}\sum_{i \in \mathcal{N}} x_{i, n+1, k} \leq |\mathcal{V}| k∈V∑j∈N∑x0jk=k∈V∑i∈N∑xi,n+1,k≤∣V∣
(3)运输载重限制
由于经典的 VRPTW 问题在满足客户点需求时,是不断地在消耗车辆的载重,因此车辆载重变化是呈现非增递减的趋势,因此只要一开始的载重量满足要求,则后续车辆到达各个客户点时载重量都是符合要求的,具体约束如下:
∑ i ∈ C d i ∑ j ∈ N x i j k ≤ q ∀ k ∈ V \sum_{i \in \mathcal{C}} d_i \sum_{j \in \mathcal{N}} x_{i j k} \leq q \quad \forall k \in \mathcal{V} i∈C∑dij∈N∑xijk≤q∀k∈V
(4)时间相关约束
前面提到,为了使得车辆到达各个客户点的时间满足时间窗要求,我们设置了简介决策变量 s s s,而该变量的具体取值,取决于我们的车辆行驶路线,因此,需要用约束把这种关系表示出来,如下:
x i j k ( s i k + t i j − s j k ) ≤ 0 ∀ i , j ∈ N , ∀ k ∈ V x_{i j k}\left(s_{i k}+t_{i j}-s_{j k}\right) \leq 0 \quad \forall i, j \in \mathcal{N}, \forall k \in \mathcal{V} xijk(sik+tij−sjk)≤0∀i,j∈N,∀k∈V
显然的,该表示是出现了决策变量相乘的非线性形式,其中一方变量为布尔变量,该类型的逻辑约束能够通过大 M 法转换为线性表达式,具体如下:
s i k + t i j − M i j ( 1 − x i j k ) ≤ s j k ∀ i , j ∈ N , ∀ k ∈ V s_{ik}+t_{ij}-M_{ij}(1-x_{ijk})\leq s_{jk}\quad \forall i,j\in\mathcal{N},\forall k \in \mathcal{V} sik+tij−Mij(1−xijk)≤sjk∀i,j∈N,∀k∈V
其中, M M M 是一个极大的常数值,该约束的含义是,当 x i j k = 1 x_{ijk}=1 xijk=1 时,说明车辆 k k k 直接从节点 i i i 移动到节点 j j j,此时车辆到达 i , j i,j i,j 的时间间隔不小于两个节点间的转运时间 t i j t_{ij} tij;反之,如果 x i j i k = 0 x_{ijik}=0 xijik=0,则该约束恒成立,即约束无效。这里的 M M M 的取值会对求解效率有一定的影响,一般尽量取紧凑的值,假设车辆 k k k 从节点 i i i 到达节点 j j j,由于一直有 a i ≤ s i k ≤ b i a_i \leq s_{ik} \leq b_i ai≤sik≤bi,可得:
→ a i + t i j ≤ s i + t i j ≤ b i + t i j \rightarrow a_i+t_{ij}\leq s_i+t_{ij}\leq b_i+t_{ij} →ai+tij≤si+tij≤bi+tij
由于 s i + t i j ≤ s j s_i+t_{ij}\leq s_j si+tij≤sj,因此 s i + t i j − s j ≤ 0 s_i+t_{ij}-s_j\leq 0 si+tij−sj≤0,找到最紧凑的 M M M 值,即找到 s i + t i j − s j s_i+t_{ij}-s_j si+tij−sj 的上界值,简单画图可知,当 s j s_j sj 严格大于 s i + t i j s_i+t_{ij} si+tij 时,说明车辆到早了,发生了等待,因此等待时间越短,则得到的 s i + t i j − s j s_i+t_{ij}-s_j si+tij−sj 的上界值越大,最短的等待时间即 b i + t i j − a j b_i+t_{ij}-a_j bi+tij−aj,遍历取最大值(绝对值最小)得到, s i + t i j − s j s_i+t_{ij}-s_j si+tij−sj 不会大于 m a x { b i + t i j − a j } , ∀ ( i , j ) ∈ A max\{b_i+t_{ij}-a_j\},\forall (i,j)\in A max{bi+tij−aj},∀(i,j)∈A,具体为什么取紧凑的大 M M M 对求解效率有影响可以参考文章《避免大M取值过大引起的数值问题》。
2.3 目标函数
VRPTW 的目标函数可以根据具体情况进行设置,而本文引用的模型的目标是使总旅行成本最小化,具体如下:
min ∑ k ∈ V ∑ i ∈ N ∑ j ∈ N c i j x i j k \min \sum_{k \in \mathcal{V}} \sum_{i \in \mathcal{N}} \sum_{j \in \mathcal{N}} c_{i j} x_{i j k} mink∈V∑i∈N∑j∈N∑cijxijk
即最小化所有车辆的所有途径路线的代价(成本或距离)
值得讨论的一个问题是,如果车辆 k k k 不启用,那么变量 s i k , ∀ i ∈ C s_{ik},\forall i\in C sik,∀i∈C 的取值大小。由于在求解模型前对决策变量的取值并不清楚,因此需要对所有可能的情况进行覆盖建模,此时 s i k s_{ik} sik 可能表示的是一个未启用车辆到达各个客户点的时间,该时间为空,但在模型优化中,它会被取特定的值。有以下两种处理方式:
- 把没启用的车辆,或者是车辆不负责该客户点的 s i k s_{ik} sik 设置为 0 0 0,该约束的实现需要判断车辆 k k k 是否服务于客户点 i i i,该逻辑约束复杂性较高;
- 不管车辆 k k k 是否会服务于 i i i,都将 s i k s_{ik} sik 视为会正常服务,只需要增加约束 a i ≤ s i k ≤ b i a_i\leq s_{ik}\leq b_i ai≤sik≤bi。根据前面的“时间相关约束”的说明,在这种处理方式下,如果车辆 k k k 没有从节点 i i i 到节点 j j j,那么车辆在两个节点的到达时间不受约束,会在 [ a I , b i ] [a_I, b_i] [aI,bi] 当中任取,那么,对于这种无关的变量的任取行为,是否会影响目标函数值呢?显然不会,因此,为了方便建模,采用该方式处理是可行的。
那有人会问,如果目标函数中包含有最小化运输时间,最小化服务结束时间等与时间有关的项时,是否还能用这种建模方式呢?大家可以思考一下
3. 利用pyscipopt库进行求解
这里的案例数据取 C101.txt 的数据,为了方便演示(过多客户点过于复杂),这里只取其中的前
25
25
25 个节点进行演示求解。
为了方便相关变量及参数能够在求解 VRPTW 问题的全局都可以调用,可以将该问题定义为一个类,实例化该类形成一个具体的待求问题。
class VRPTW(object):
def __int__(self, c_num, v_num, cap, x, y, demand, a, b, service):
self.customerNum, self.vehicleNum, self.capacity = c_num, v_num, cap
self.cor_X, self.cor_Y, self.demand, self.readyTime, self.dueTime, self.serviceTime = x, y, demand, a, b, service
self.disMatrix = [[]] # 距离矩阵
基于Solomon数据的模型与上述模型有一些区别,在Solomon数据当中,给出了各个节点的坐标位置,以及客户点的服务时间,默认车辆的移动速度为 1 1 1 单位时间移动 1 1 1 单位距离,以及默认单位距离的运输成本为 1 1 1,因此目标为最小化总的运输距离。
具体步骤及说明如下:
3.1 读入数据并实例化 vrp 问题
这里只取 C101.txt 数据的前
25
25
25 个客户点。关于 Solomon 标准数据的格式介绍可以参考 VRPTW问题的Solomon标准测试数据集介绍。
cus_num = 25 # 顾客点数量
with open('C101.txt') as file:
lines = file.readlines()
# 第5行 NUMBER CAPACITY
vehicleNum, capacity = list(map(int, re.split(r" +", lines[4].strip()))) # 车辆数,车容量
# 第10行到最后一行分别存储. CUST NO, XCOORD, YCOORD, DEMAND, READY TIME, DUE DATE, SERVICE TIME
cust_data = np.array([list(map(int, re.split(r" +", i.strip()))) for i in lines[9:10+cus_num]])
cor_X = cust_data[:, 1] # 节点 x 轴坐标
cor_Y = cust_data[:, 2] # 节点 y 轴坐标
demand = cust_data[:, 3] # 节点需求(起始点需求为0)
readyTime = cust_data[:, 4] # 节点时间窗左边界
dueTime = cust_data[:, 5] # 节点时间窗右边界
serviceTime = cust_data[:, 6] # 节点服务时间(起始点服务时间为0)
vrp = VRPTW(cus_num, cus_num, capacity, cor_X, cor_Y, demand, readyTime, dueTime, serviceTime)
3.2 数据预处理
在建模时,由于环路消除约束的存在,常常需要复制一个起始点的虚拟点,来使得车辆最终回到初始点,实际的含义不变,但在模型当中需要复制一个新的节点。这种方式比较直观简单,还有另一种在工程化过程的方式,就是对约束的范围以及变量的范围稍加限制即可,由于目标函数中并无时间相关的项,因此形成路径环并不影响最终的结果。
该部分的预处理对初步传入的数据进行整理,主要是计算距离矩阵,以及紧凑的大 M M M 值,其中大 M M M 值要考虑上服务时间,代码如下:
def prepare_date(self):
self.disMatrix = np.full((self.customerNum + 1, self.customerNum + 1), 0)
M = np.full((self.customerNum + 1, self.customerNum + 1), 0)
for i in range(self.customerNum + 1):
for j in range(self.customerNum + 1):
if i != j:
self.disMatrix[i, j] = math.sqrt((self.cor_X[i] - self.cor_X[j]) ** 2 + (self.cor_Y[i] - self.cor_Y[j]) ** 2)
M[i, j] = self.dueTime[i] + self.disMatrix[i, j] - self.readyTime[j]
self.bigM = np.max(M) + max(self.serviceTime)
3.3 建模并求解
了解一个求解器的建模接口最快的方式就是看一个简单的混合整数建模例子,可以参考 基于Python调用SCIP求解器的入门文档,了解 pyscipopt 库的基本调用接口。具体到本文的 VRPTW 案例的建模如下:
def solve_vrptw(self):
model= scip.Model()
# ==========定义变量==========
x, s = {}, {}
for i in range(self.customerNum + 1):
for j in range(self.customerNum + 1):
if (i != j) and (i + j > 0):
for k in range(self.vehicleNum):
x[i, j, k] = model.addVar(vtype='B', name=f'x_{i}{j}{k}')
for i in range(self.customerNum + 1):
for k in range(self.vehicleNum):
s[i, k] = model.addVar(vtype='C', name=f's_{i}{k}')
# ==========定义约束==========
## 约束1:流平衡约束
for i in range(1, self.customerNum + 1):
model.addCons(scip.quicksum(x[i, j, k] for j in range(self.customerNum + 1) for k in range(self.vehicleNum) if i!=j) == 1,
name=f'customer_depart_{i}')
model.addCons(scip.quicksum(x[j, i, k] for j in range(self.customerNum + 1) for k in range(self.vehicleNum) if i!=j) == 1,
name='customer_enter_{i}')
## 约束2:车辆的进出流平衡
for k in range(self.vehicleNum):
for i in range(1, self.customerNum + 1):
model.addCons(scip.quicksum(x[i, j, k] for j in range(self.customerNum + 1) if i!=j) ==
scip.quicksum(x[j, i, k] for j in range(self.customerNum + 1) if i!=j), name=f'flow_{k}{i}')
## 约束3:启用的车辆数平衡
model.addCons(scip.quicksum(x[0, j, k] for j in range(1, self.customerNum + 1) for k in range(self.vehicleNum)) ==
scip.quicksum(x[j, 0, k] for j in range(1, self.customerNum + 1) for k in range(self.vehicleNum)), name='dispatch')
## 约束4:车辆载重限制
for k in range(self.vehicleNum):
model.addCons(scip.quicksum(self.demand[i] * x[i, j, k] for i in range(1, self.customerNum + 1) for j in range(self.customerNum + 1) if i!=j) <= self.capacity,
name=f'capacity_vehicle_{k}')
## 约束5:前后节点时间关系
for k in range(self.vehicleNum):
for i in range(self.customerNum + 1):
for j in range(1, self.customerNum + 1):
if (i != j) and (i + j > 0):
model.addCons(s[i,k] + self.serviceTime[i] + self.disMatrix[i,j] <= s[j,k] + self.bigM * (1 - x[i,j,k]))
model.addCons(s[i,k] + self.serviceTime[i] + self.disMatrix[i,j] <= self.dueTime[0])
## 约束6:时间窗约束
for k in range(self.vehicleNum):
model.addCons(s[0, k] == 0)
for i in range(1, self.customerNum + 1):
model.addCons(s[i, k] >= self.readyTime[i])
model.addCons(s[i, k] <= self.dueTime[i])
# ==========定义目标==========
model.setObjective(scip.quicksum(x[i, j, k] * self.disMatrix[i, j] for (i, j, k) in x))
model.setMinimize()
model.optimize()
# ==========输出结果==========
print('model_status = ', model.getStatus())
print('model_gap =', model.getGap())
print('model_obj =', model.getObjVal())
# model.writeProblem('vrpTW.lp')
vrptw_route = []
for k in range(self.vehicleNum):
for i in range(self.customerNum + 1):
for j in range(self.customerNum + 1):
if (i != j) and (i + j > 0):
if model.getVal(x[i,j,k]) > 0:
vrptw_route.append((i,j,k))
print('vrptw_route:\n', vrptw_route)
# 绘制结果路径
self.plt_route_pic(vrptw_route)
上述方法是 VRPTW 类的一个成员方法,模型中最关键的约束函数与前面对约束的介绍逐一对应,方便读者能够对照理解,尽管部分循环的写法过于冗余。最后求解得到的车辆配送路线 ( i , j , k ) (i,j,k) (i,j,k) 集合如下:
[(12, 0, 0), (0, 13, 1), (0, 20, 1), (12, 0, 1), (13, 17, 1), (14, 12, 1), (15, 16, 1), (16, 14, 1), (17, 18, 1), (18, 19, 1), (19, 15, 1), (20, 24, 1), (21, 0, 1), (22, 21, 1), (23, 22, 1), (24, 25, 1), (25, 23, 1), (0, 5, 2), (1, 0, 2), (2, 1, 2), (3, 7, 2), (4, 2, 2), (5, 3, 2), (6, 4, 2), (7, 8, 2), (8, 10, 2), (9, 6, 2), (10, 11, 2), (11, 9, 2), (0, 13, 4), (12, 0, 4), (13, 17, 4), (14, 12, 4), (15, 16, 4), (16, 14, 4), (17, 18, 4), (18, 19, 4), (19, 15, 4)]
通过调用另一个成员方法 plt_route_pic 展示路线图:
def plt_route_pic(self, vrp_route):
plt.figure(figsize=(10, 8))
# 绘制坐标的散点图
for i in range(self.customerNum + 1):
if i == 0:
plt.scatter(self.cor_X[i], self.cor_Y[i], marker='^', c='r')
plt.annotate('depot', (self.cor_X[i], self.cor_Y[i]))
else:
plt.scatter(self.cor_X[i], self.cor_Y[i], marker='o', c='black')
plt.annotate(str(i), (self.cor_X[i], self.cor_Y[i]))
# 绘制箭头
for idx in vrp_route:
i,j,k = idx
plt.arrow(self.cor_X[i], self.cor_Y[i], self.cor_X[j] - self.cor_X[i], self.cor_Y[j] - self.cor_Y[i],
length_includes_head = True, head_width =0.5, head_length=0.8, fc='red', ec='red',linewidth=0.3)
plt.xlabel('x')
plt.ylabel('y')
plt.title('VRPTW')
plt.show()
plt.savefig('vrptw.png')
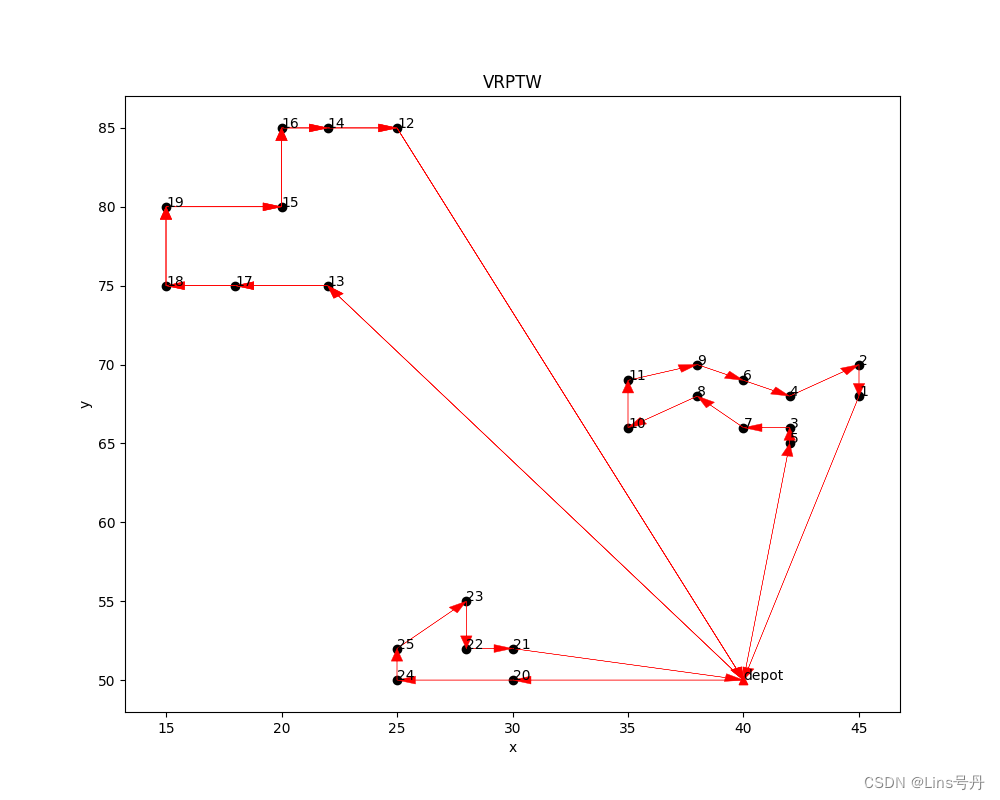
该案例的求解时间
18.93
s
18.93s
18.93s,求解到最优值,目标值为:
187
187
187。






















 1938
1938











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










