强化学习（二）马尔科夫决策过程(MDP)

强化学习（二）马尔科夫决策过程(MDP)

参考：https://www.cnblogs.com/pinard/p/9426283.html

在强化学习（一）模型基础中，我们讲到了强化学习模型的8个基本要素。但是仅凭这些要素还是无法使用强化学习来帮助我们解决问题的, 在讲到模型训练前，模型的简化也很重要，这一篇主要就是讲如何利用马尔科夫决策过程(Markov Decision Process，以下简称MDP)来简化强化学习的建模。

1. 强化学习引入MDP的原因

强化学习的8个要素我们在第一节已经讲了。其中的第七个是环境的状态转化模型，它可以表示为一个概率模型，即在状态s下采取动作a,转到下一个状态s′的概率，表示为$P_{s{s}^{\prime }}^a$
如果按照真实的环境转化过程看，转化到下一个状态$s$′的概率既与上一个状态$s$有关，还与上上个状态，以及上上上个状态有关。这一会导致我们的环境转化模型非常复杂，复杂到难以建模。因此我们需要对强化学习的环境转化模型进行简化。简化的方法就是假设状态转化的马尔科夫性，也就是假设转化到下一个状态$s\prime$的概率仅与上一个状态s有关，与之前的状态无关。用公式表示就是：
$$P_{s{s}^{\prime }}^a=E(S_{t+1}=s^{\prime }|S_t=s,A_t=a)$$

除了对于环境的状态转化模型这个因素做马尔科夫假设外，我们还对强化学习第四个要素个体的策略$(policy)\pi$也做了马尔科夫假设。即在状态s时采取动作a的概率仅与当前状态s有关，与其他的要素无关。用公式表示就是
$$\pi (a|s)=P(A_t=a|S_t=s)$$
对于第五个要素，价值函数$v_{\pi }(s)$也是一样，$v_{\pi }(s)$现在仅仅依赖于当前状态了，那么现在价值函数$v_{\pi }(s)$可以表示为：
$$v_{\pi }(s)=E(G_t|S_t=s)=E_{\pi }(R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...|S_t=s)$$
其中$G_t$表示收获$return$，是一个MDP中从某一个状态$S_t$开始采样直到终止状态是所有奖励的衰减之和。

2. MDP的价值函数与贝尔曼方程

对于MDP。我们在第一节降到了他的价值函数$v_{\pi }(s)$的表达式。但是这个表达是没有考虑到所采用动作a带来的价值影响，因此我们除了$v_{\pi }(s)$这个状态函数外，还有一个动作价值函数$q_{\pi }(s,a)$，即：
$$q_{\pi }(s,a)=E(G_t|S_t=s,A_t=a)=E_{\pi }(R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...|S_t=s,A_t=a)$$
根据价值函数的表达式，我们可以推倒出价值函数基于状态的递推关系，比如对于状态价值函数$v_{\pi }(s)$，可以发现：
$$\begin{array}{rl}{v}_{\pi }(s)& =E_{\pi }(R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...|S_t=s)\\ & =E_{\pi }(R_{t+1}+\gamma (R_{t+2}+\gamma R_{t+3}+...)|S_t=s)\\ & =E_{\pi }(R_{t+1}+\gamma G_{t+1}|S_t=s)\\ & =E_{\pi }(R_{t+1}+\gamma v_{\pi }(S_{t+1})|S_t=s)\end{array}$$
也就是说，在t时刻的状态$S_t$和t+1时刻的状态$S_{t+1}$是满足递推关系的，即：
$$v_{\pi }(s)=E_{\pi }(R_{t+1}+\gamma v_{\pi }(S_{t+1})|S_t=s)$$
这个递推式子我们一般将它叫做贝尔曼方程。这个式子告诉我们，一个状态的价值由该状态的奖励以及后续状态价值按一定的衰减比例联合组成。

同样的方法，我们可以得到动作价值函数$q_{\pi }(s,a)$的贝尔曼方程：
$$q_{\pi }(s,a)=E_{\pi }(R_{t+1}+\gamma q_{\pi }(S_{t+1},A_{t+1})|S_t=s,A_t=a)$$

3. 状态价值函数与动作价值函数的递推关系

根据动作价值函数$q_{\pi }(s,a)$和状态价值函数$v_{\pi }(s)$的定义，我们很容易得到他们之间的转化关系公式：
$$v_{\pi }(s)=\sum _{a\in A}\pi (a|s)q_{\pi }(s,a)$$
也就是说，状态价函数是所有动作价值函数基于策略$\pi$的期望。通俗说就是某状态下所有状态动作价值乘以该动作出现的概率，最后求和，就得到了对应的状态价值。
反过来，利用贝尔曼方程，我们很容易从状态价值函数$v_{\pi }(s)$表示动作价值函数$q_{\pi }(s,a)$,即：
$$q_{\pi }(s,a)=R_s^a+\gamma \sum _{s^{\prime }\in S}{P}_{s{s}^{\prime }}^a{v}_{\pi }(s^{\prime })$$
通俗说就是状态动作价值由两部分相加组成，第一部分是即时奖励，第二部分是环境所有可能的下一个状态的概率乘以该下一个状态的状态值，最后求和，并加上衰减。
转化过程如图所示：
把上面两个式子结合起来，我们可以得到：
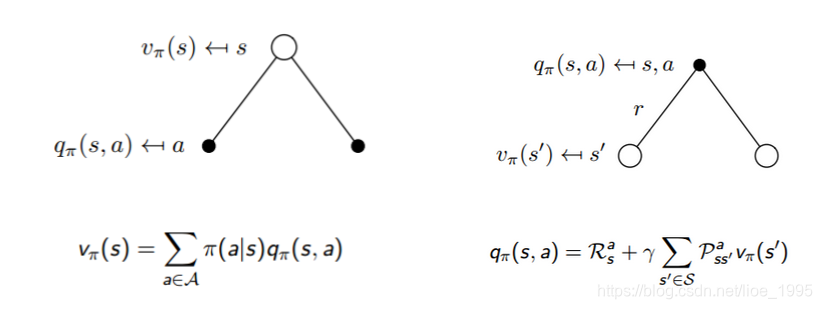
$$v_{\pi }(s)=\sum _{a\in A}\pi (a|s)(R_s^a+\gamma \sum _{s\in s^{\prime }}{P}_{s{s}^{\prime }}^a{v}_{\pi }(s^{\prime }))$$
$$q_{\pi }(s,a)=R_s^a+\gamma \sum _{s^{\prime }\in S}{P}_{s{s}^{\prime }}^a\sum _{a^{\prime }\in A}\pi (a^{\prime }|s^{\prime })q_{\pi }(s^{\prime },a^{\prime })$$

4.最优价值函数

解决强化学习问题意味着要寻找一个最优的策略让个体在与环境交互过程中获得始终比其它策略都要多的收获，这个最优策略我们可以用 ${\pi }^{\ast }$表示。一旦找到这个最优策略${\pi }^{\ast }$，那么我们就解决了这个强化学习问题。一般来说，比较难去找到一个最优策略，但是可以通过比较若干不同策略的优劣来确定一个较好的策略，也就是局部最优解。
如何比较策略的优劣呢？一般是通过对应的价值函数来比较的，也就是说，寻找较优策略可以通过寻找较优的价值函数来完成。可以定义最优状态价值函数是所有策略下产生的众多状态价值函数中的最大者，即：
$$v_{\ast }(s)=\underset{\pi }{\max }{v}_{\pi }(s)$$
同理也可以定义最优动作价值函数是所有策略下产生的中多动作状态价值函数中的最大值，即：
$$q_{\ast }(s,a)=\underset{\pi }{\max }{q}_{\pi }(s,a)$$
对于最优的策略，基于动作价值函数我们可以定义为：
$${\pi }_{\ast }(a|s)=\{\begin{array}{l}1,ifa=argma{x}_{a\in A}{q}_{\ast }(s,a)\\ 0,else\end{array}$$
只要我们找到了最大的状态价值函数或者动作价值函数，那么对应的策略${\pi }^{\ast }$就是我们强化学习问题的解。同时利用状态价值函数和动作价值函数之间的关系，我们可以得到：
$$v_{\ast }(s)=\underset{a}{\max }{q}_{\ast }(s,a)$$
反过来的最优价值函数关系也很容易得到：
$$q_{\ast }(s,a)=R_s^a+\gamma \sum _{s^{\prime }\in S}{P}_{s{s}^{\prime }}^a{v}_{\ast }(s^{\prime })$$
利用上面两个式子也可以得到和第三届每位类似的式子：
$$v_{\ast }(s)=\underset{a}{\max }(R_s^a+\gamma \sum _{s^{\prime }\in S}{P}_{s{s}^{\prime }}^a{v}_{\ast }(s^{\prime }))$$
$$q_{\ast }(s,a)=R_s^a+\gamma \sum _{s^{\prime }\in S}{P}_{s{s}^{\prime }}^a\underset{a^{\prime }}{\max }{q}_{\ast }(s^{\prime },a^{\prime })$$

5.MDP实例

这是一个例子，图中左下那个圆圈位置是七点，方框位置是终点。上面动作有study，pub，facebook，quit，sleep，每个状态对应的及时奖励R已经标出来了。我们的目标是找到最优的动作价值函数或者状态价值函数，进而找出最优策略。
为了方便，我们假设衰减因子γ=1，$\pi (a|s)=0.5$.
对于终点方框位置，由于没有下一个状态，也没有当前状态的动作，因此状态价值函数为0。其余四个状态，我们一次定义其价值为$v_1,v_2,v_3,v_4$，分别对应左上，左下，中下，右上位置的圆圈，我们基于$v_{\ast }(s)={\max }_a(R_s^a+\gamma {\sum }_{s^{\prime }\in S}{P}_{s{s}^{\prime }}^a{v}_{\ast }(s^{\prime }))$计算所有状态价值函数，可以得到一个方程组：
对于位置$v_1$,我们有：$v_1=0.5\ast (-1+v_1)+0.5\ast (0+v_2)$
对于位置$v_2$,我们有：$v_2=0.5\ast (-1+v_1)+0.5\ast (-2+v_3)$
对于位置$v_3$,我们有：$v_3=0.5\ast (0+0)+0.5\ast (-2+v_4)$
对于位置$v_4$,我们有：$v_4=0.5\ast (10+0)+0.5\ast (1+0.2\ast v_2+0.4\ast v_3+0.4\ast v_4)$
求得$v_1=-2.3,v_2=-1.3,v_3=2.7,v_4=7.4$每个状态的价值函数如下所示：
上面我们固定了策略$\pi (a|s)$，虽然求出了每个状态的状态价值函数，但是并不一定是最优价值函数。那么如何求出最优价值函数呢？这里有与状态机简单，求出最优的状态价值该函数$v_{\ast }(s)$或者动作价值函数$q_{\ast }(s,a)$比较容易。
我们这次以动作价值函数$q_{\ast }(s,a)$为例求解，首先终点方框处的好求。
$$q_{\ast }(s_3,sleep)=0,q_{\ast }(s_4,study)=10$$
接着利用$$q_{\ast }(s,a)=R_s^a+\gamma \sum _{s^{\prime }\in S}{P}_{s{s}^{\prime }}^a\underset{a^{\prime }}{\max }{q}_{\ast }(s^{\prime },a^{\prime })$$
列方程组求出所有的$q_{\ast }(s,a)$。有了所有的$q_{\ast }(s,a)$，利用
$$v_{\ast }(s)=\underset{a}{\max }{q}_{\ast }(s,a)$$
就可以求出所有的$v_{\ast }(s)$。最终求出所有$v_{\ast }(s)$和$q_{\ast }(s,a)$如下图所示：

从而我们的最优决策路径是走6->6->8->10->结束

6. MDP小结

MDP是强化学习入门的关键一步，如果这部分研究的比较清楚，后面的学习就会容易很多。因此值得多些时间在这里。虽然MDP可以直接用方程组来直接求解简单的问题，但是更复杂的问题却没有办法求解，因此我们还需要寻找其他有效的求解强化学习的方法。