leetcode 84.Largest Rectangle in Histogram(Hard)
Problem:
Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.
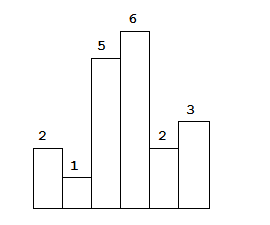
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].
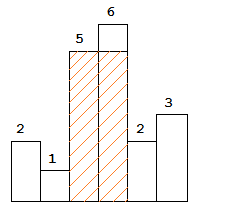
The largest rectangle is shown in the shaded area, which has area = 10 unit.
Example:
Given heights = [2,1,5,6,2,3],
return 10.
Algorithm:
方法一:显然,最大面积矩形的高即为条形图中某一元素的高度。因此,较为直接的做法是枚举所有的元素,以其高度作为矩形的高度,再尽可能地往左往右延伸,取最大长度为矩形的宽度,最后选出所有矩形中的最大值,即为我们所求的答案。由于算法复杂度为O(n^2),本题会导致超时
方法二:我们注意到以下几点特征:
(1)若条形图元素高度依次递增,假设条形图中共有n个元素,则以第i个元素(i = 0,1,2…)作为高的最大矩形的宽度必然为n - i,因为它只能往右边延伸且能延伸到最右端。也就是说,以其作为高的最大矩形面积为h[i] * (n - i),这样,我们只需要以每个元素为高计算面积,再选出最大者即可,时间复杂度为O(n)。
(2)在上述条形图的基础上,假设我们在其中两个元素i,j之间插入一系列元素(假设插入的元素也满足依次递增),且每个新插入元素的高度均大于i和j的高度。显然,如果整个图最大矩形的高为新插入元素中任意一个的高度,则矩形最大宽度必定不会超过新插入的这组元素个数,因为i,j的高度均比它们的小。这时,我们可以把新插入的元素组看成一个新的条形图,进行步骤1的处理即可得到最大矩形面积。如果最大矩形高度不属于新插入的元素,则最大矩形的算法与步骤1相同,只是以i及i左边的元素作为高的最大矩形宽度有所改变(新宽 = 原宽 + 新插入元素个数)
(3)注意,步骤2中的i可以不存在,即往原条形图的左侧插入新元素,这种情况与步骤2中的分析是相同的。
(4)多次重复步骤2或3,即可得到参差不齐的条形图及计算最大矩形的方法
方法二实现方法:
(1)用一个栈来存储元素下标,在原条形图最右侧插入高度为0的元素作为结束标志。
(2)从左往右遍历每个条形图元素,若该元素的高度大于栈顶元素的高度,则将其入栈。也就是说,我们保证栈中元素高度依次递增
(3)若遍历到某一元素i的高度小于栈顶元素高度,则弹出栈中所有比它高的元素。所有弹出的元素等价于方法二步骤2中新插入的元素(注意,这些元素满足依次递增)。我们把这些弹出的元素看成一个新的条形图,计算出其最大矩形面积(用方法二中步骤1的方法),与当前所记录的最大面积进行比较更新。
(4)令该元素i入栈,重复步骤2,直到遍历完所有元素。
(5)因为条形图最后一个元素为0,所以原条形图中的所有元素必会经历步骤3的过程。而0对最大面积不造成影响,因此算法是正确的。该方法的时间复杂度为O(n)
Code:
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
heights.push_back(0); //条形图后面补0
stack<int> s;
s.push(0);
int smax = 0;
for(int i = 1; i < heights.size(); ++ i) {
//将满足递增关系的元素入栈
while(heights[i] > heights[s.top()]) {
s.push(i);
++ i;
}
//弹出所有不满足的元素,更新最大面积
while(heights[i] < heights[s.top()]) {
int cindex = s.top();
s.pop();
if(s.empty()){
smax = max(smax, heights[cindex] * i);
break;
}
smax = max(smax, heights[cindex] * (i - s.top() - 1));
}
s.push(i);
}
return smax;
}
};leetcode 85.Maximal Rectangle(Hard)
Problem:
Given a 2D binary matrix filled with 0’s and 1’s, find the largest rectangle containing only 1’s and return its area.
Example:
given the following matrix:
1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0
Return 6
Algorithm:
该题思路与leetcode 84相似,我们用矩阵中的每一行及其以上各行生成一个柱形图,求出最大面积,再求出所有柱形图中的面积最大者即可。
Code:
class Solution {
public:
//leetcode 84
int largestRectangleArea(vector<int>& heights) {
heights.push_back(0);
stack<int> s;
s.push(0);
int smax = 0;
for(int i = 1; i < heights.size(); ++ i) {
while(heights[i] > heights[s.top()]) {
s.push(i);
++ i;
}
while(heights[i] < heights[s.top()]) {
int cindex = s.top();
s.pop();
if(s.empty()){
smax = max(smax, heights[cindex] * i);
break;
}
smax = max(smax, heights[cindex] * (i - s.top() - 1));
}
s.push(i);
}
return smax;
}
//leetcode 85
int maximalRectangle(vector<vector<char>>& matrix) {
if(matrix.size() == 0) return 0;
vector<int> v(matrix[0].size());
int mmax = 0;
for(int i = 0; i < matrix.size(); ++ i) {
for(int j = 0; j < matrix[i].size(); ++ j) {
if(matrix[i][j] == '1') v[j] ++;
else v[j] = 0;
}
mmax = max(mmax, largestRectangleArea(v));
}
return mmax;
}
};




















 7569
7569

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








