基于遗传与免疫两种算法求解生产节拍物料搬运问题
文章目录
1.问题描述
某汽车装配线物料供应布局如图1,在物料超市内,零部件按照品种和工作站划分,存放在货架上。拖车在物料超市装载料箱,并沿着特定的路线行驶,依次经过6个工作站的14种零件存放处,在需补货的零件位置卸载,执行完一次搬运任务回到超市,等待下一次搬运。在给定装配计划期内,待组装的不同车型按照装配序列依次进人装配线,零件包装在标准料箱中,根据各个车型的BOM表能够计算出此段装配计划期内各种零件的总料箱需求。

考虑一个简单的混流装配线,生产三种车型M1,M2,M3,消耗三种零件P1,P2,P3,每个工作站包含一种零件。假定装配序列为<1 1 2 3 2>,可以计算出此段装配计划期内每个生产节拍的零件需求,零件以料箱的形式运送到工作站,详见表1。根据计算,此段装配计划期内,零件P1,P2,P3需求分别为2.1,2个料箱,则可获得此段装配计划期内每个生产节拍的零件料箱需求见表2。
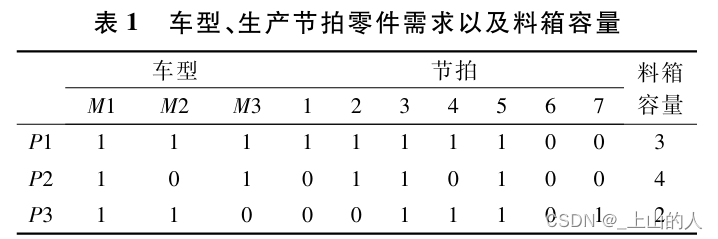
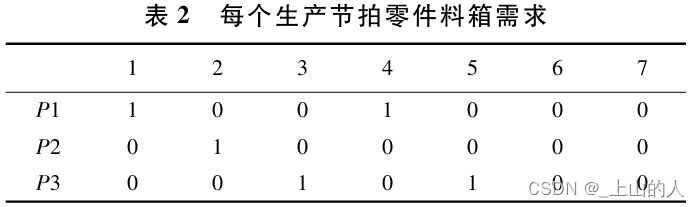
因为车道狭窄和车间运力能力有限,每次搬运携带不超过拖车容量的料箱。此外,由于车道的固定,拖车只能匀速行驶,不能掉头或者中断。因此:本文设立如下假设条件:
(1)仅有一辆牵引拖车,无设备故障,在其路线上勾速行驶,搬运的行驶时间恒定
(2)零件包装在标准料箱中,牵引拖车在物料超市装载料箱,在工作站零件点卸载料箱,需要、定装、卸载时间,且时间相同。
(3)牵引拖车的搬运过程不可中断,当车辆从物料超市出发,在固定路线上行驶,必须处理完所有的搬运任务,执行完整的工作循环,才能回到超市。
(4)牵引拖车容量有限,每次装载的料箱数量不能超过其容量限制,对于每种零件,一次搬运只能装载一个料箱,不允许重复装载。准时化配送在给定装配计划期内,根据工作站的物料需求和消耗时间,为避免零件缺货,需要确定每次搬运的零件种类、搬运的最佳开始时间以及到达搬运零件位置的时间。
2 符号定义
集合
P
p
P_p
Pp 零件类型集合
n
n
n 搬运次数集合
M
+
M^+
M+ 生产节拍集合
索引
p
p
p 零件类型下标
p
∈
P
p
p \in P_p
p∈Pp
n
n
n 搬运次数下标
n
∈
N
n \in N
n∈N
m
m
m 产品序列下标
m
∈
M
+
m \in M^+
m∈M+
参数
l
l
l 在超市装载一个满箱零件的时间
r
r
r 在零件库存点卸载一个满箱零件的时间
B
p
m
B_{pm}
Bpm 装配第 m 公生产节拍对零件 p 的需求
C
+
C_+
C+ 一个参数(车辆能够承载的最大零件批数量的数量)
h
p
h_p
hp 超市到零件 p 的行驶时间
h
o
p
1
hop1
hop1 初始时刻零件 p 的库存量
t
t
e
x
t
s
t
a
r
t
t_{ text{start}}
ttextstart 物料搬运调度开始的时刻
t
t
e
x
t
e
n
d
t_{ text{end}}
ttextend 物料搬运调度结束的时刻
z
1
z_1
z1 足够大的整数
z
2
z_2
z2 足够小的整数
Q
p
2
Q_{p2}
Qp2 一个满箱零件 p 的数量
c
+
t
c^t_+
c+t 装配线的生产节拍
T
n
T_n
Tn 一次搬运行驶的时间
决策变量
y p n y_{pn} ypn 0-1 变量,第 n 次搬运是否产生
3 模型
目标函数
为了降低搬运成本,本文在充分利用多载量小车容量的前提下采用最少的搬运次数来进行物料搬运,而搬运次数可以通过多载量小车容量的变化来调整。根据零件箱总需求及零件捆车容量,可以计算出最少搬运次数 N min N_{\text{min}} Nmin 为:
N min = ⌈ ∑ p = 1 P p ( ∑ m = 1 M + B p m ⋅ h o p 1 c + p ) C + ⌉ N_{\text{min}} = \left\lceil \frac{\sum_{p=1}^{P_p} \left( \sum_{m=1}^{M^+} \frac{B_{pm} \cdot hop1}{c_{+p}} \right)}{C_+} \right\rceil Nmin= C+∑p=1Pp(∑m=1M+c+pBpm⋅hop1)
在给定的搬运次数下,以最小化工作站零件库存和最小化搬运次数为目标,由于工作站库存和搬运次数之间的耦合关系十分复杂,故在不同优化目标前添加了不同的权重,体现了不同目标函数的优先级别。目标函数如下
Min ( α ⋅ ∑ m = 1 M + ∑ p = 1 P p H m p + β ⋅ ∑ n = 1 N y n ) \text{Min} \left( \alpha \cdot \sum_{m=1}^{M^+} \sum_{p=1}^{P_p} H_{mp} + \beta \cdot \sum_{n=1}^{N} y_n \right) Min α⋅m=1∑M+p=1∑PpHmp+β⋅n=1∑Nyn
约束条件
α = 1 0 3 , β = 1 0 − 3 \alpha = 10^3, \beta = 10^{-3} α=103,β=10−3
H m p = h o p 1 + ∑ n = 1 N e n m p × Q p − ∑ i = 1 m + 1 B p i ∀ n ∈ N , m ∈ M , p ∈ P (3-3) H_{mp} = hop1 + \sum_{n=1}^{N} e_{nmp} \times Q_p - \sum_{i=1}^{m+1} B_{pi} \quad \forall n \in N, m \in M, p \in P \quad \text{(3-3)} Hmp=hop1+∑n=1Nenmp×Qp−∑i=1m+1Bpi∀n∈N,m∈M,p∈P(3-3)
∑ p = 1 P X n p ≤ y n × C ∀ n ∈ N (3-4) \sum_{p=1}^{P} X_{np} \leq y_n \times C \quad \forall n \in N \quad \text{(3-4)} ∑p=1PXnp≤yn×C∀n∈N(3-4)
t n + 1 ≥ t n + T + r × ∑ p = 1 P X n p + l × ∑ p = 1 P X ( n + 1 ) p ∀ n = 1 , … , N − 1 (3-5) t_{n+1} \geq t_n + T + r \times \sum_{p=1}^{P} X_{np} + l \times \sum_{p=1}^{P} X_{(n+1)p} \quad \forall n = 1, \ldots, N-1 \quad \text{(3-5)} tn+1≥tn+T+r×∑p=1PXnp+l×∑p=1PX(n+1)p∀n=1,…,N−1(3-5)
t n ≥ t 0 ∀ n ∈ N (3-6) t_n \geq t_0 \quad \forall n \in N \quad \text{(3-6)} tn≥t0∀n∈N(3-6)
t n + r × ∑ p = 1 P X n p + T × f n ≤ t e ∀ n ∈ N (3-7) t_n + r \times \sum_{p=1}^{P} X_{np} + T \times f_n \leq t_e \quad \forall n \in N \quad \text{(3-7)} tn+r×∑p=1PXnp+T×fn≤te∀n∈N(3-7)
t n p ′ = t n + d p + r × ∑ q = 1 P X n q ∀ n ∈ N , p ∈ P (3-8) t'_{np} = t_n + d_p + r \times \sum_{q=1}^{P} X_{nq} \quad \forall n \in N, p \in P \quad \text{(3-8)} tnp′=tn+dp+r×∑q=1PXnq∀n∈N,p∈P(3-8)
D n p = ∑ m = 1 M B p m × z n m p ∀ n ∈ N , ∀ p ∈ P (3-9) D_{np} = \sum_{m=1}^{M} B_{pm} \times z_{nmp} \quad \forall n \in N, \forall p \in P \quad \text{(3-9)} Dnp=∑m=1MBpm×znmp∀n∈N,∀p∈P(3-9)
m ∗ c t − t n p ′ ≤ Z ( n + 1 ) p × G ∀ n ∈ N , ∀ p ∈ P , ∀ m ∈ M − 1 (3-10) m^*ct - t'_{np} \leq Z_{(n+1)p} \times G \quad \forall n \in N, \forall p \in P, \forall m \in M-1 \quad \text{(3-10)} m∗ct−tnp′≤Z(n+1)p×G∀n∈N,∀p∈P,∀m∈M−1(3-10)
t n p ′ − m ∗ c t + g ≤ Z n ( l ) p × G ∀ n ∈ N , ∀ p ∈ P (3-11) t'_{np} - m^*ct + g \leq Z_{n(l)p} \times G \quad \forall n \in N, \forall p \in P \quad \text{(3-11)} tnp′−m∗ct+g≤Zn(l)p×G∀n∈N,∀p∈P(3-11)
c t − t n p ′ ≤ Z n ( l ) p × G ∀ n ∈ N , ∀ p ∈ P (3-12) ct - t'_{np} \leq Z_{n(l)p} \times G \quad \forall n \in N, \forall p \in P \quad \text{(3-12)} ct−tnp′≤Zn(l)p×G∀n∈N,∀p∈P(3-12)
t n p ′ − c t + g ≤ ∑ Z n ( l ) p × G ∀ n ∈ N , ∀ p ∈ P (3-13) t'_{np} - ct + g \leq \sum Z_{n(l)p} \times G \quad \forall n \in N, \forall p \in P \quad \text{(3-13)} tnp′−ct+g≤∑Zn(l)p×G∀n∈N,∀p∈P(3-13)
z n m p + Z n m p ′ = 1 ∀ n ∈ N , ∀ p ∈ P , ∀ m ∈ M (3-14) z_{nmp} + Z'_{nmp} = 1 \quad \forall n \in N, \forall p \in P, \forall m \in M \quad \text{(3-14)} znmp+Znmp′=1∀n∈N,∀p∈P,∀m∈M(3-14)
m ∗ c t − t n p ′ + g ≥ u n m p × G ∀ n ∈ N , ∀ p ∈ P , ∀ m ∈ M (3-15) m^*ct - t'_{np} + g \geq u_{nmp} \times G \quad \forall n \in N, \forall p \in P, \forall m \in M \quad \text{(3-15)} m∗ct−tnp′+g≥unmp×G∀n∈N,∀p∈P,∀m∈M(3-15)
t n p ′ − m ∗ c t ≤ ( 1 − u n m p ) × G ∀ n ∈ N , ∀ p ∈ P , ∀ m ∈ M (3-16) t'_{np} - m^*ct \leq (1 - u_{nmp}) \times G \quad \forall n \in N, \forall p \in P, \forall m \in M \quad \text{(3-16)} tnp′−m∗ct≤(1−unmp)×G∀n∈N,∀p∈P,∀m∈M(3-16)
2 e n m p ≤ X n p + u n m p ∀ n ∈ N , ∀ p ∈ P (3-17) 2e_{nmp} \leq X_{np} + u_{nmp} \quad \forall n \in N, \forall p \in P \quad \text{(3-17)} 2enmp≤Xnp+unmp∀n∈N,∀p∈P(3-17)
1 + e n m p ≥ X n p + u n m p ∀ n ∈ N , ∀ p ∈ P , ∀ m ∈ M (3-18) 1 + e_{nmp} \geq X_{np} + u_{nmp} \quad \forall n \in N, \forall p \in P, \forall m \in M \quad \text{(3-18)} 1+enmp≥Xnp+unmp∀n∈N,∀p∈P,∀m∈M(3-18)
h 0 p + ∑ j = 1 N Q p × X j p − D n p ≥ 0 ∀ n ∈ N , ∀ p ∈ P (3-19) h_{0p} + \sum_{j=1}^{N} Q_p \times X_{jp} - D_{np} \geq 0 \quad \forall n \in N, \forall p \in P \quad \text{(3-19)} h0p+∑j=1NQp×Xjp−Dnp≥0∀n∈N,∀p∈P(3-19)
h 0 p + ∑ n = 1 N Q p × X n p − ∑ m = 1 M B p m ≥ 0 ∀ n ∈ N , ∀ p ∈ P , ∀ m ∈ M (3-20) h_{0p} + \sum_{n=1}^{N} Q_p \times X_{np} - \sum_{m=1}^{M} B_{pm} \geq 0 \quad \forall n \in N, \forall p \in P, \forall m \in M \quad \text{(3-20)} h0p+∑n=1NQp×Xnp−∑m=1MBpm≥0∀n∈N,∀p∈P,∀m∈M(3-20)
H m p ≥ 0 ∀ p ∈ P , ∀ m ∈ M (3-21) H_{mp} \geq 0 \quad \forall p \in P, \forall m \in M \quad \text{(3-21)} Hmp≥0∀p∈P,∀m∈M(3-21)
t 0 ≤ t n p ′ ≤ t e ∀ n ∈ N , ∀ p ∈ P (3-22) t_0 \leq t'_{np} \leq t_e \quad \forall n \in N, \forall p \in P \quad \text{(3-22)} t0≤tnp′≤te∀n∈N,∀p∈P(3-22)
D
n
p
≥
0
∀
n
∈
N
,
∀
p
∈
P
(3-23)
D_{np} \geq 0 \quad \forall n \in N, \forall p \in P \quad \text{(3-23)}
Dnp≥0∀n∈N,∀p∈P(3-23)
在上述模型中,优化目标 (3-2) 最小化每个节拍后各种零件的线边库存总和以及最小搬运次数。
约束 (3-3) 表示第 m 个节拍后零件 p 的库存;
约束 (3-4) 保证零件捆车在每次搬运过程中装载的料箱数量不超过它的搬运能力;
约束 (3-5) 保证相邻两次搬运的时间不重叠;
约束 (3-6) - (3-7) 限定每次搬运的开始时间;
约束 (3-8) 计算第 n 次搬运零件 p 的送达时刻;
约束 (3-9) - (3-14) 计算零件 p 在第 n 次搬运送达时的总消耗量。引入 0-1 变量
z
n
m
p
z_{nmp}
znmp 和
z
(
m
+
1
)
p
′
z'_{(m+1)p}
z(m+1)p′ 来确定第 n 次搬运送达时所处的节拍数范围,来辅助确定物料需求量
D
n
p
D_{np}
Dnp;
约束 (3-15) - (3-18) 确定零件 p 在节拍 m 内送达可用,用
X
n
p
X_{np}
Xnp 和
u
n
m
p
u_{nmp}
unmp 来确定
e
n
m
p
e_{nmp}
enmp 的范围;
约束 (3-19) 保证上一次数搬运发生后的所有零件不缺货;
约束 (3-20) 使得初始库存和搬运的零件总数量满足装配产品所需的零件总数;
约束 (3-21) - (3-23) 为约束变量的取值范围。
4 算例分析
4.1 算例描述
D 汽车公司总装车间生产线上可生产 K、S、X 三种车型。物料超市服务生产线 38 个工作站(工作站 22-59),该物料超市由 5 个送料工位负责向生产线作坊搬运物料,以其中一个送料工位 43509 为例,该岗位负责其中的 4 个工作站,负责 21 种不同的零件 P1-P21,在作坊具体的布局见图 3.1。生产线的生产节拍为 112s,车型拖车依次经过 21 种零件的储存位置,速度为 3m/s,行驶的路线总长为 450m。装载一个空箱料箱的时间为 40s,卸载一个空箱料箱的时间为 35s。某个阶段订单生产时将以批量生产,不在超过设备产能瓶颈的情况下,会优先考虑总相同车型和材质集中排产,便于控制生产过程中过程设备切换的成本。车型生产序列均按照 K i , K j , K l K_i, K_j, K_l Ki,Kj,Kl 和 S h , S k , S t S_h, S_k, S_t Sh,Sk,St 和 X r , X s , X t X_r, X_s, X_t Xr,Xs,Xt 等三种车型带“i”的车型为高配车型, K 1 , S 1 , X 1 K_1, S_1, X_1 K1,S1,X1 等三种车型带“I”的车型为低配置车型,同一种车型不同配置相应的车型物料清单 BOM 也会有所不同。表 1 列出了三种车型不同配置的物料清单 BOM,每种车型的空箱料箱的包装量为 Q,每种车型对应的工作站存位物料超市的距离为 D。
| P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 | P10 | P11 | P12 | P13 | P14 | P15 | P16 | P17 | P18 | P19 | P20 | P21 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| k h k_h kh车型 | 2 | 1 | 2 | 1 | 1 | 1 | 2 | 1 | 2 | 1 | 3 | 1 | 1 | 2 | 3 | 4 | 2 | 2 | 3 | 2 | 3 |
| k l k_l kl车型 | 2 | 1 | 2 | 1 | 1 | 1 | 2 | 1 | 2 | 1 | 0 | 1 | 1 | 1 | 3 | 1 | 2 | 2 | 1 | 2 | 2 |
| S h S_h Sh车型 | 2 | 2 | 4 | 2 | 3 | 2 | 2 | 2 | 1 | 1 | 2 | 3 | 2 | 3 | 2 | 2 | 3 | 2 | 4 | 2 | 3 |
| S l S_l Sl车型 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 1 | 3 | 2 | 3 | 2 | 2 | 3 | 2 | 3 | 2 | 4 |
| X h X_h Xh车型 | 2 | 2 | 4 | 2 | 3 | 2 | 2 | 2 | 2 | 3 | 2 | 1 | 2 | 3 | 2 | 3 | 2 | 4 | 3 | 2 | 1 |
| X l X_l Xl车型 | 2 | 1 | 4 | 2 | 2 | 2 | 2 | 2 | 3 | 3 | 2 | 1 | 1 | 3 | 2 | 3 | 2 | 3 | 3 | 1 | 1 |
| D / M D/M D/M | 102 | 104 | 105 | 108 | 110 | 212 | 215 | 217 | 218 | 222 | 331 | 333 | 334 | 337 | 340 | 404 | 405 | 408 | 410 | 411 | 415 |
4.2 算法求解
4.2.1 遗传算法求解
遗传算法的流程不再赘述,这里直接上matlab的代码
选择操作
function [xx,A]=xuanze(x,f,gap)%选择
%采用轮盘赌法选择个体
%目标函数值越差的概率越大
f1=f;
f1=1./f1;
f1=mapminmax(f1',0,1)';
f1=f1+0.01;
f1=sum(f1,2);
A=[];
xx=x(A,:);
交叉操作
function xx=jiaocha(xx,pcross,N,canshu,f)%交叉函数
%单点交叉操作
if nargin<5
p=pcross(1);
end
x1=xx;
for i=1:size(xx,1)
if nargin==5
f1=f;
end
if rand<p
flag=0;
while flag==0
a=randi([1,size(xx,1)]);
b=randi([1,size(xx,2)-1]);
xx(i,:)=[x1(i,1:b),x1(a,b+1:end)];
P=[];%统计每个车次的搬运
for j=1:N
P(j,1)=numel(find(xx(i,:)==j));
end
end
end
end
变异操作
function xx=bianyi(xx,pmutation,N,canshu,f)
%变异操作
if nargin<5
p=pmutation(1);
end
for i=1:size(xx,1)
if nargin==5
f1=f;
end
if rand<p
flag=0;
while flag==0
xx(i,:)=randi([1,N],1,size(xx,2));%产生随机变量
P=[];%统计每个车次的搬运
if isempty(find(P>canshu.C))==1%不超过车辆最大载量
flag=1;
end
end
end
end
计算适应度
function [f,Z,T,ZZ,TT]=fitness(x,X,N,L,canshu)
Z=zeros(N,max(X));%记录每次搬运的物料箱数
T=zeros(N,1);%记录每次搬运的时间
for i=1:N
b=find(Z(i,:)>0);%小车经过的节点
for j=1:length(b)
%计算节点之间的行程
if j==1
T(i,1)=T(i,1)+canshu.D(b(j))/canshu.v;
end
%计算取货时间
T(i,1)=T(i,1)+Z(i,b(j))*canshu.t1;
end
%返回起点时间
T(i,1)=T(i,1)+canshu.D(b(end))/canshu.v;
%卸箱时间
T(i,1)=T(i,1)+sum(Z(i,:))*canshu.t2;
end
T1=cumsum(T);%物流补充的时间点
m=1;%第几次补充
ZZ=[];%记录每个产品生产后的剩余物料
TT=zeros(length(L),1);%计算每个产品的加工时间(如果物料不足则需等待车辆运送足够物流再进行生产)
for i=1:length(L)
if i==1
if isempty(find(canshu.h0-canshu.BOM(L(i),:)<0))==1
ZZ=[ZZ;canshu.h0-canshu.BOM(L(i),:)];
TT(i,1)=canshu.t3;
end
else
if isempty(find(ZZ(end,:)-canshu.BOM(L(i),:)<0))==1
ZZ=[ZZ;ZZ(end,:)-canshu.BOM(L(i),:)];
TT(i,1)=TT(i-1,1)+canshu.t3;
end
end
end
f=canshu.a*sum(ZZ,'all')+canshu.b*N;
择优操作
function exc=excellence(f,Concentration,i,ps)
% 计算个体繁殖概率
% individuals input 种群
% M input 种群规模
% ps input 多样性评价参数
% exc output 繁殖概率
fit = 1./f;
fit = mapminmax(fit',0,1)';
sumfit = sum(fit);
con = Concentration;
sumcon = sum(con);
exc = fit(i)/sumfit*ps +con(i)/sumcon*(1-ps); %exc为当前每个个体的一个评价值
相似度
function concentration = concentration(i,M,x)
% 计算个体浓度值
% i input 第i个抗体
% M input 种群规模
% x input 个体
% concentration output 浓度值
concentration=0;
for j=1:M
xsd=similar(x(i,:),x(j,:)); % 第i个体与种群所有个体间的相似度
% 相似度大于阀值就说明相似
if xsd>0.7
concentration=concentration+1;
end
end
concentration=concentration/M;%计算相似度
end
主函数(GA算法)
clear
clc
close all
tic
%% 模型参数设置
canshu=fun_data;
L=canshu.L;%生产序列
W=ceil(max((sum(canshu.BOM(L,:),1)-canshu.h0),0)./canshu.Q);%每种零件需要搬运的物料箱数
N=ceil(sum(W)/canshu.C);
X=[];%将所需的每个物料箱视为任务,构建任务集
for i=1:length(W)
X=[X,i.*ones(1,W(i))];
end
dim=length(X);
%% 遗传算法参数设置
sizepop=100;%种群规模
MAXGEN=100;%迭代次数
gap=0.9;%选择率
pcross=0.3;%遗传过程中的交叉概率
pmutation=0.1;%遗传过程中的变异概率
%% 初始化种群
x=[];%记录变量
f=[];%记录目标函数
for i=1:sizepop
flag=0;
while flag==0
x(i,:)=randi([1,N],1,dim);%产生随机变量
P=[];%统计每个车次的搬运
end
f(i,1)=fitness(x(i,:),X,N,L,canshu);
end
%记录最优
[bestf,o]=min(f);
bestx=x(o,:);
trace=[bestf];
%% 迭代寻优
for ii=1:MAXGEN
%选择
[xx,A]=xuanze(x,f,gap);
%交叉
xx=jiaocha(xx,pcross,N,canshu);
%变异
xx=bianyi(xx,pmutation,N,canshu);
%计算新的目标函数值
ff=[];
for i=1:size(xx,1)
ff(i,1)=fitness(xx(i,:),X,N,L,canshu);
%更新个体
end
%更新最优
if min(f)<bestf
[bestf,o]=min(f);
bestx=x(o,:);
end
trace=[trace;bestf];
end
%迭代曲线
figure
plot([0:MAXGEN],trace,'LineWidth',2)
xlabel('迭代次数')
ylabel('目标函数值')
title('遗传算法迭代曲线')
legend('最优值')
%最优解
[~,Z,T,ZZ,TT]=fitness(bestx,X,N,L,canshu);
result_Z=[["批次\物料种类",1:size(Z,2),"所需时间/s"];[[1:N]',Z,round(T)]];
result_ZZ=[["生产序列\物料剩余量",1:size(Z,2),"生产时间/s"];[L',ZZ,round(TT)]];
fprintf('目标函数值:%.4f\n',bestf)
fprintf('每批次不同物料箱装车数量:')
disp(result_Z)
fprintf('每个生产节拍后的物流剩余量:')
disp(result_ZZ)
%甘特图
figure
hold on
for i=1:size(TT)
t0=(i-1)*canshu.t3;
t1=TT(i,1)-canshu.t3;
t2=TT(i,1);
x0=[t0,t1,t1,t0,t0];
x1=[t1,t2,t2,t1,t1];
y1=[i-0.3,i-0.3,i+0.3,i+0.3,i-0.3];
fill(x0,y1,'b','FaceAlpha',0.3,'EdgeColor','none')
fill(x1,y1,'g','FaceAlpha',0.3,'EdgeColor','none')
text(TT(i,1)-canshu.t3,i,["车型"+L(i)],'color','r','FontSize',8)
end
xlabel('时间/s')
yticks([1:size(TT,1)])
ylim([0,size(TT,1)+1])
ylabel('生产序列')
legend('延迟时间段','生产时间段','location','northwest')
save result1
toc
4.2.2 遗传算法结果分析
结果图如下



| 物料种类\批次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 3 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 8 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 12 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 13 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 14 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 15 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 16 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 17 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 18 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 19 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 20 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 21 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 所需时间/s | 66 | 71 | 89 | 93 | 94 | 93 | 93 |
| 物料剩余量\生产序列 | 1 | 1 | 1 | 3 | 5 | 2 | 2 | 2 | 4 | 6 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 8 | 6 | 4 | 2 | 0 | 8 | 6 | 4 | 2 | 0 |
| 2 | 11 | 10 | 9 | 7 | 5 | 4 | 3 | 2 | 12 | 11 |
| 3 | 13 | 11 | 9 | 5 | 1 | 14 | 12 | 10 | 8 | 4 |
| 4 | 9 | 8 | 7 | 5 | 3 | 2 | 11 | 10 | 8 | 6 |
| 5 | 17 | 16 | 15 | 12 | 9 | 8 | 7 | 6 | 4 | 2 |
| 6 | 14 | 13 | 12 | 10 | 8 | 7 | 6 | 5 | 3 | 1 |
| 7 | 10 | 8 | 6 | 4 | 2 | 0 | 10 | 8 | 6 | 4 |
| 8 | 7 | 6 | 5 | 3 | 1 | 8 | 7 | 6 | 4 | 2 |
| 9 | 8 | 6 | 4 | 13 | 11 | 9 | 7 | 5 | 3 | 0 |
| 10 | 14 | 13 | 12 | 11 | 8 | 7 | 6 | 5 | 4 | 1 |
| 11 | 15 | 12 | 9 | 7 | 5 | 5 | 5 | 5 | 4 | 2 |
| 12 | 9 | 8 | 7 | 4 | 3 | 2 | 1 | 0 | 7 | 6 |
| 13 | 11 | 10 | 9 | 7 | 5 | 16 | 15 | 14 | 12 | 11 |
| 14 | 6 | 4 | 2 | 7 | 4 | 3 | 2 | 1 | 6 | 3 |
| 15 | 7 | 4 | 1 | 9 | 7 | 14 | 11 | 8 | 6 | 4 |
| 16 | 11 | 7 | 3 | 16 | 13 | 12 | 11 | 10 | 8 | 5 |
| 17 | 10 | 8 | 6 | 3 | 1 | 11 | 9 | 7 | 4 | 2 |
| 18 | 18 | 16 | 14 | 12 | 8 | 6 | 4 | 2 | 20 | 17 |
| 19 | 21 | 18 | 15 | 11 | 8 | 7 | 6 | 5 | 26 | 23 |
| 20 | 16 | 14 | 12 | 10 | 8 | 6 | 4 | 2 | 18 | 17 |
| 21 | 12 | 9 | 6 | 3 | 2 | 0 | 13 | 11 | 7 | 6 |
| 生产时间/s | 112 | 224 | 336 | 448 | 560 | 672 | 784 | 896 | 1008 | 1120 |
4.2.3 免疫遗传算法求解
在免疫遗传算法中添加如下步骤

主函数(IA算法)
clear
clc
close all
tic
%% 模型参数设置
canshu=fun_data;
L=canshu.L;%生产序列
W=ceil(max((sum(canshu.BOM(L,:),1)-canshu.h0),0)./canshu.Q);%每种零件需要搬运的物料箱数
N=ceil(sum(W)/canshu.C);
X=[];%将所需的每个物料箱视为任务,构建任务集
for i=1:length(W)
X=[X,i.*ones(1,W(i))];
end
dim=length(X);
%% 免疫算法参数设置
sizepop=100;%种群规模
overbest=30;%记忆库容量大小
MAXGEN=100;%迭代次数
gap=0.9;%选择率
pcross=[0.1,0.5];%免疫细胞遗传过程中的自适应交叉概率
pmutation=[0.05,0.3];%免疫细胞遗传过程中的自适应变异概率
ps=0.7;% 多样性评价参数
number=sizepop+overbest;
%% 初始化种群
x=[];%记录变量
f=[];%记录目标函数
for i=1:number
flag=0;
while flag==0
x(i,:)=randi([1,N],1,dim);%产生随机变量
P=[];%统计每个车次的搬运
if isempty(find(P>canshu.C))==1%不超过车辆最大载量
flag=1;
end
end
f(i,1)=fitness(x(i,:),X,N,L,canshu);
end
%记录最优
[bestf,o]=min(f);
bestx=x(o,:);
trace=[bestf];
%% 迭代寻优
for ii=1:MAXGEN
Concentration=[];
%计算个体浓度
Excellence=[];
%计算繁殖概率
%繁殖概率排序
[~,o]=sort(Excellence,'descend');
%更新记忆库(将个体较好的储存记忆库)
Jf=f(o(1:overbest),:);
Jx=x(o(1:overbest),:);
%选择
[xx,A]=xuanze(x,f,gap);
%交叉
xx=jiaocha(xx,pcross,N,canshu,f);
%变异
xx=bianyi(xx,pmutation,N,canshu,f);
%计算新的目标函数值
ff=[];
for i=1:size(xx,1)
ff(i,1)=fitness(xx(i,:),X,N,L,canshu);
%更新个体
if ff(i,1)<f(A(i),1)
f(A(i),1)=ff(i,1);
x(A(i),:)=xx(i,:);
end
end
%加入记忆库
fl=[f;Jf];
xl=[x;Jx];
%更新最优
if min(f)<bestf
[bestf,o]=min(fl);
bestx=xl(o,:);
end
trace=[trace;bestf];
end
%迭代曲线
figure
plot([0:MAXGEN],trace,'LineWidth',2)
xlabel('迭代次数')
ylabel('目标函数值')
title('免疫算法迭代曲线')
legend('最优值')
%最优解
[~,Z,T,ZZ,TT]=fitness(bestx,X,N,L,canshu);
result_Z=[["批次\物料种类",1:size(Z,2),"所需时间/s"];[[1:N]',Z,round(T)]];
result_ZZ=[["生产序列\物料剩余量",1:size(Z,2),"生产时间/s"];[L',ZZ,round(TT)]];
fprintf('目标函数值:%.4f\n',bestf)
fprintf('每批次不同物料箱装车数量:')
disp(result_Z)
fprintf('每个生产节拍后的物流剩余量:')
disp(result_ZZ)
%甘特图
figure
hold on
for i=1:size(TT)
t0=(i-1)*canshu.t3;
t1=TT(i,1)-canshu.t3;
t2=TT(i,1);
x0=[t0,t1,t1,t0,t0];
x1=[t1,t2,t2,t1,t1];
y1=[i-0.3,i-0.3,i+0.3,i+0.3,i-0.3];
fill(x0,y1,'b','FaceAlpha',0.3,'EdgeColor','none')
fill(x1,y1,'g','FaceAlpha',0.3,'EdgeColor','none')
text(TT(i,1)-canshu.t3,i,["车型"+L(i)],'color','r','FontSize',8)
end
xlabel('时间/s')
yticks([1:size(TT,1)])
ylim([0,size(TT,1)+1])
ylabel('生产序列')
legend('延迟时间段','生产时间段','location','northwest')
save result2
toc
4.2.4 人工免疫遗传算法结果分析


| 物料种类\批次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 8 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 9 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 12 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 13 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 14 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 15 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 16 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 17 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 18 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 19 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 20 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 21 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 所需时间/s | 93 | 81 | 94 | 93 | 67 | 93 | 71 |
| 物料剩余量\生产序列 | 1 | 1 | 1 | 3 | 5 | 2 | 2 | 2 | 4 | 6 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 8 | 6 | 4 | 2 | 0 | 8 | 6 | 4 | 2 | 0 |
| 2 | 11 | 10 | 9 | 7 | 5 | 4 | 3 | 2 | 0 | 11 |
| 3 | 13 | 11 | 9 | 5 | 1 | 14 | 12 | 10 | 8 | 4 |
| 4 | 9 | 8 | 7 | 5 | 3 | 12 | 11 | 10 | 8 | 6 |
| 5 | 17 | 16 | 15 | 12 | 9 | 8 | 7 | 6 | 4 | 2 |
| 6 | 14 | 13 | 12 | 10 | 8 | 7 | 6 | 5 | 3 | 1 |
| 7 | 10 | 8 | 6 | 4 | 2 | 12 | 10 | 8 | 6 | 4 |
| 8 | 7 | 6 | 5 | 3 | 1 | 8 | 7 | 6 | 4 | 2 |
| 9 | 8 | 6 | 4 | 3 | 1 | 9 | 7 | 5 | 3 | 0 |
| 10 | 14 | 13 | 12 | 11 | 8 | 7 | 6 | 5 | 4 | 1 |
| 11 | 15 | 12 | 9 | 7 | 5 | 5 | 5 | 5 | 4 | 2 |
| 12 | 9 | 8 | 7 | 4 | 3 | 12 | 11 | 10 | 7 | 6 |
| 13 | 11 | 10 | 9 | 7 | 5 | 4 | 3 | 2 | 0 | 11 |
| 14 | 6 | 4 | 2 | 7 | 4 | 3 | 2 | 9 | 6 | 3 |
| 15 | 7 | 4 | 1 | 9 | 7 | 4 | 1 | 8 | 6 | 4 |
| 16 | 11 | 7 | 3 | 16 | 13 | 12 | 11 | 10 | 8 | 5 |
| 17 | 10 | 8 | 6 | 3 | 1 | 11 | 9 | 7 | 4 | 2 |
| 18 | 18 | 16 | 14 | 12 | 8 | 6 | 4 | 2 | 0 | 17 |
| 19 | 21 | 18 | 15 | 11 | 8 | 7 | 6 | 5 | 2 | 23 |
| 20 | 16 | 14 | 12 | 10 | 8 | 6 | 4 | 2 | 0 | 17 |
| 21 | 12 | 9 | 6 | 3 | 2 | 15 | 13 | 11 | 7 | 6 |
| 生产时间/s | 112 | 224 | 336 | 448 | 560 | 672 | 784 | 896 | 1008 | 1120 |
4.3 遗传算法与人工免疫遗传算法对比

从迭代曲线可以看出,在遗传算法的基础上做优化操作的人工免疫遗传算法求解出的结果更优
5 总结
本文针对混流装配线准时化物料配送调度设计两种算法–遗传算法与免疫遗传算法,在该案例中,求出结果显示,在目标人工免疫遗传算法的效率比遗传算法的效率更高。
源代码整篇源代码以及说明文档都已整理好,有需要的同学可以私信或者加我V:etg243,备注来源。


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








