链接:http://hihocoder.com/problemset/problem/1069
思想:
利用dfs + ST 算法
记录下dfs的序列,还有dfs过程中每一个点的深度,对应到之前的dfs的序列中。还需要记录一个在dfs中每一个节点首次出现的位置,也是对应到dfs的那个序列中。
举个例子(画的很丑)
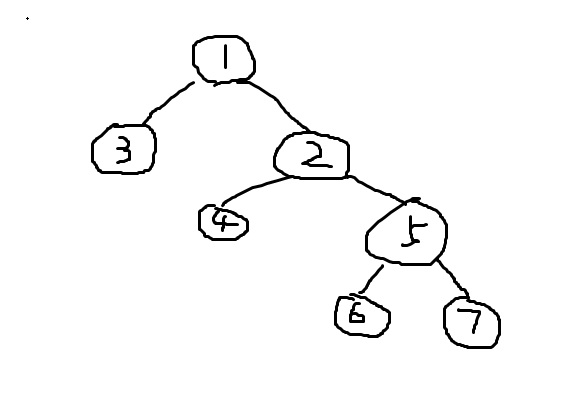
假设先去右儿子这样可以得到
dfs序列称作f : 1 2 5 7 5 6 5 2 4 2 1 3 1
深度序列称作dep: 1 2 3 4 3 4 3 2 3 2 1 2 1
首次出现序列称作first : 1 2 12 9 3 6 4
对于查询两个点之间的LCA就是各自第一次出现的路径之间一个深度最小的点。
这里就出现一个RMQ问题,在一段序列之中查找一个最小的值,所以运用了ST算法来解决这个问题
LCA(4,5) = RMQ(dep,first[4],first[7]) 将4和7的LCA 转换成求4 到 7 第一次出现的之间的序列的深度最小的值。
first[4] = 9 ,first[7] = 4 就是要求 4 3 4 3 2 3 这个序列的深度最小值, 是深度为2,对应到dfs的序列中是在第8个,返回f[8] 得到 节点 2 。
这里就是要求出的是最小值的index,然后利用这个index 在 dfs序列中对应到节点编号
代码:
hihocoder 1069:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
#include <map>
using namespace std;
#define M 500009
int dep[M],pos[M],f[M];
int in[M];
int dp[M][100];
vector<int> adj[M];
map<string,int> mp;
string name[M];
int n,m;
int tot;
void init()
{
tot = 0;
mp.clear();
memset(in,0,sizeof(in));
memset(dp,0,sizeof(dp));
for(int i = 0;i <= n;i++) adj[i].clear();
}
void dfs(int u,int pre,int depth)
{
f[++tot] = u; //dfs array which record the order
pos[u] = tot; //record the first time when a node is visited.the index mean the number of the node
dep[tot] = depth; // record the depth
for(int i = 0;i < adj[u].size();i++)
{
int v = adj[u][i];
if(v == pre) continue;
dfs(v,u,depth+1);
f[++tot] = u; // it can't be the first time,so the pos array isn't needed
dep[tot] = depth;
}
}
void st()
{
for(int i = 1;i <= tot;i++)
dp[i][0] = i; // dp[i][j] record the index of the RMQ from i to i + 2^j - 1
for(int j = 1;(1<<j) <= tot;j++)
{
for(int i = 1;i + (1<<j) - 1 <= tot;i++)
{
int mid = i + (1<<(j-1));
if(dep[dp[i][j-1]] < dep[dp[mid][j-1]]) dp[i][j] = dp[i][j-1];
else dp[i][j] = dp[mid][j-1];
}
}
}
int rmq(int l,int r)
{
l = pos[l];
r = pos[r];
if(l > r) swap(l,r);
int len = r - l + 1;
int k = (int)(log((double)len) / log(2.0));
if(dep[dp[l][k]] < dep[dp[r-(1<<k)+1][k]]) return dp[l][k];
return dp[r-(1<<k)+1][k];
}
int main()
{
//freopen("in.txt","r",stdin);
while(cin >> n)
{
init();
for(int i = 0;i < n;i++)
{
string a,b;
cin >> a >> b;
if(mp[a] == 0)
{
mp[a] = ++tot;
name[tot] = a;
}
if(mp[b] == 0)
{
mp[b] = ++tot;
name[tot] = b;
}
adj[mp[a]].push_back(mp[b]); // input the tree
in[mp[b]]++;
}
tot = 0;
for(int i = 1;i <= n;i++)
{
if(in[i] == 0)
{
dfs(i,-1,0);
break;
}
}
st();
cin >> m;
while(m--)
{
string a,b;
cin >> a >> b;
int aa = mp[a],bb = mp[b];
int ans = rmq(aa,bb); // ans is the index of the minimum in (aa,bb) of dep
cout << name[f[ans]] << endl;
}
}
return 0;
}






















 2764
2764

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








