算法导论读书笔记（23）最小生成树

第六部分 图算法

第23章 最小生成树

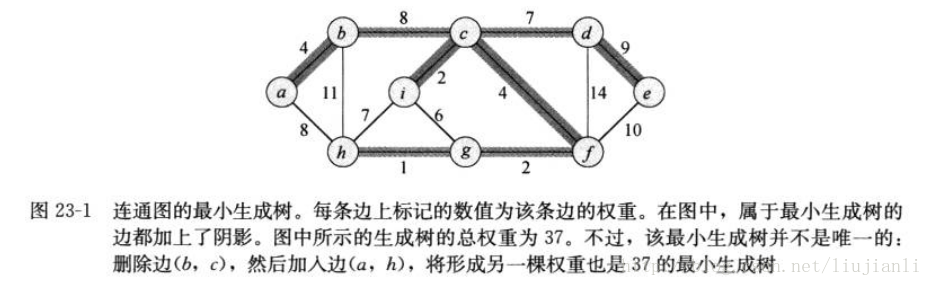
一个无环子集T⊆E，既能够将所有的结点连接起来，又具有最小的权重。由于T是无环的，并且连通所有的结点，因此，T必然是一棵树。我们称这样的树为（图G的）生成树，因为它是由图G所生成的。我们称求取该生成树的问题为最小生成树问题。

1.最小生成树的形成

在每遍循环之前，A是某棵最小生成树的一个子集。在每一步，我们要做的事情是选择一条边（u，v），将其加入到集合A中，使得A不违反循环不变式，即A∪{（u，v）}也是某棵最小生成树的子集。由于我们可以安全地将这种边加入到集合A而不会破坏A的循环不变式，因此称这样的边为集合A的安全边。

Generic-MST(G, w)
    A = ∅
    while A does not formed a spanning tree
        find and edge(u, v) that is safe for A
        A = A ∪ {(u,v)}
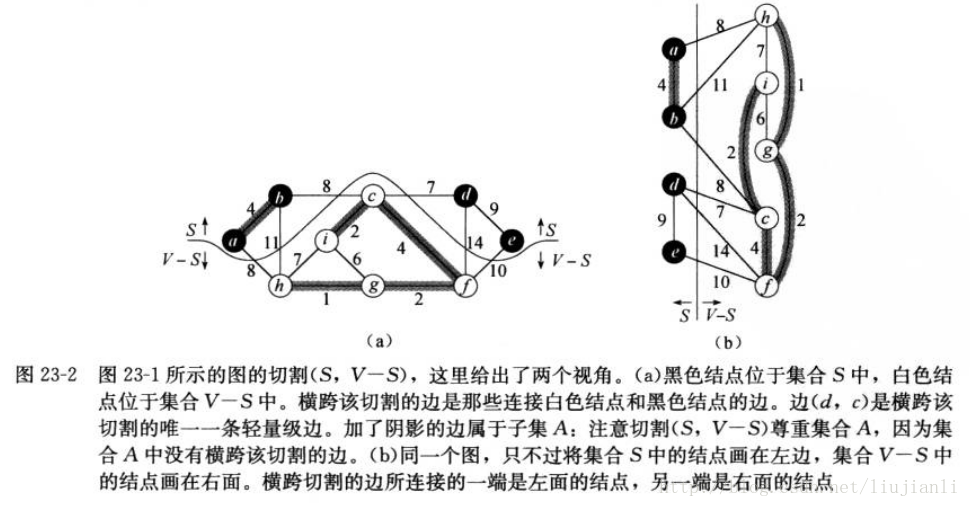
    return A

无向图G=（V，E）的一个切割（S，V-S）是集合V的一个划分。
如果一条边（u，v）∈E的一个端点位于集合S，另一个端点位于集合V-S，则称该条边横跨切割（S，V-S）。
如果集合A中不存在横跨该切割的边，则称该切割尊重集合A。
在横跨一个切割的所有边中，权重最小的边称为轻量级边。

2.Kruskal算法和Prim算法

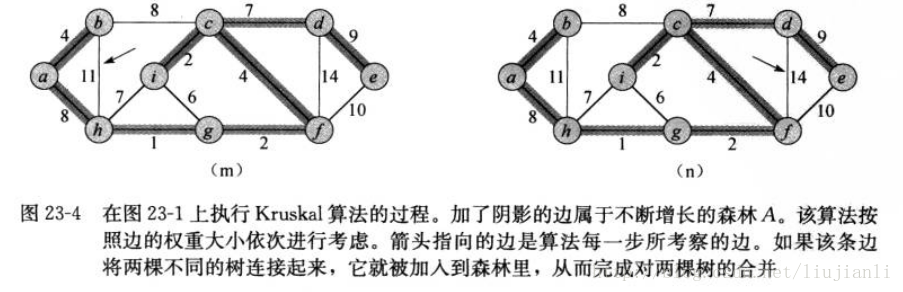
在Kruskal算法中，集合A是一个森林，其结点就是给定图的结点。每次加入到集合A中的安全边永远是权重最小的连接两个不同分量的边。在Prim算法里，集合A则是一棵树。每次加入到A中的安全边永远是连接A和A之外某个结点的边中权重最小的边。

Kruskal算法

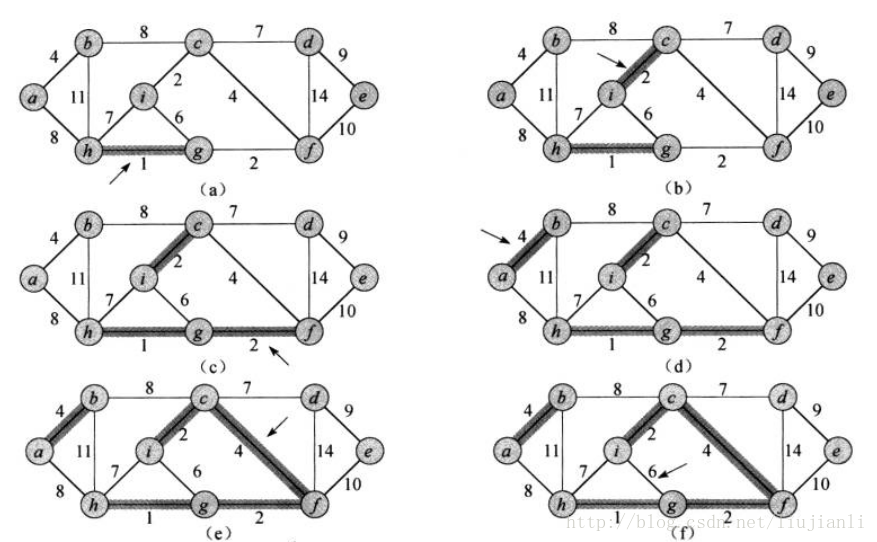
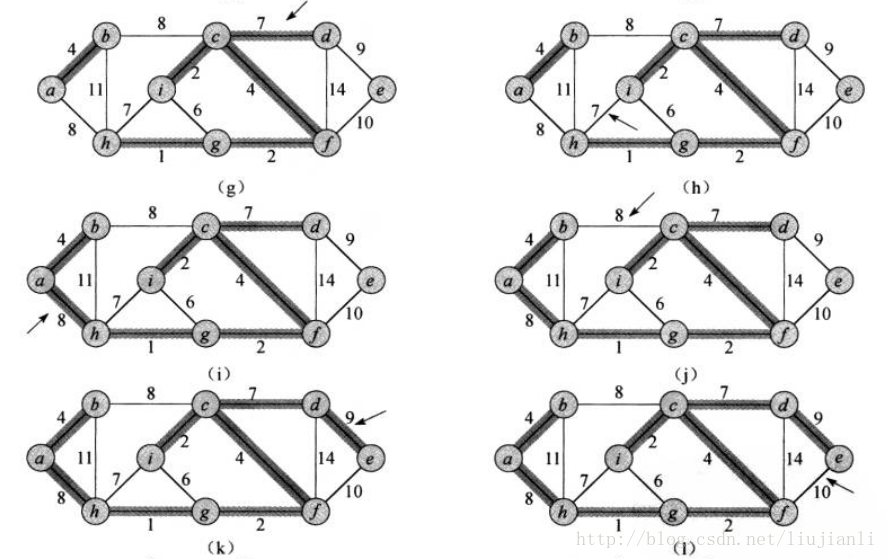
MST-Kruskal(G, w)
    A = ∅
    for each vertex v∈G.V
        Make-Set(v)
    sort the edges of G.E into nondecreasing order by weight w
    for each edge(u,v)∈G.E, taken in nondecreasing order by weight
        if Find-Set(v) != Find-Set(u)
            A = A ∪ {(u,v)}
            Union(u,v)
    return A

Kruskal算法的时间代价为O(ElgV)

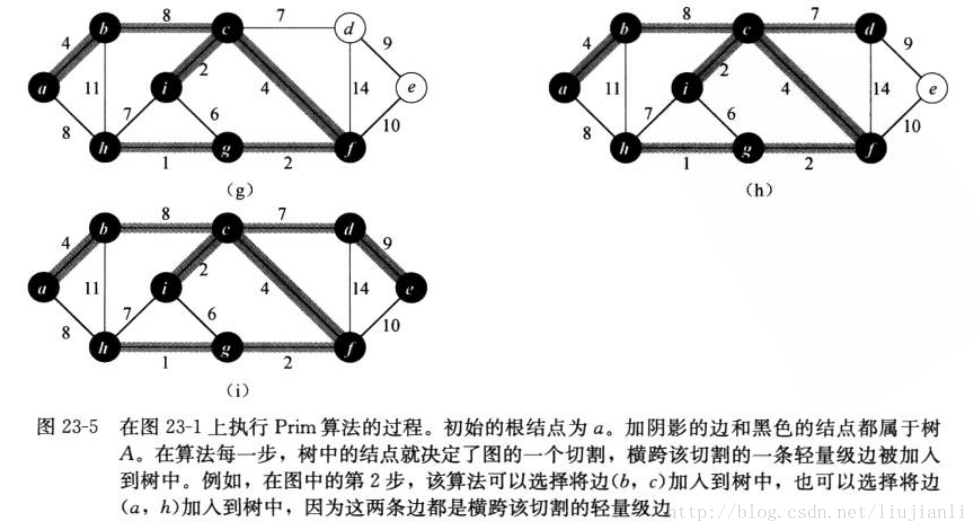
Prim算法

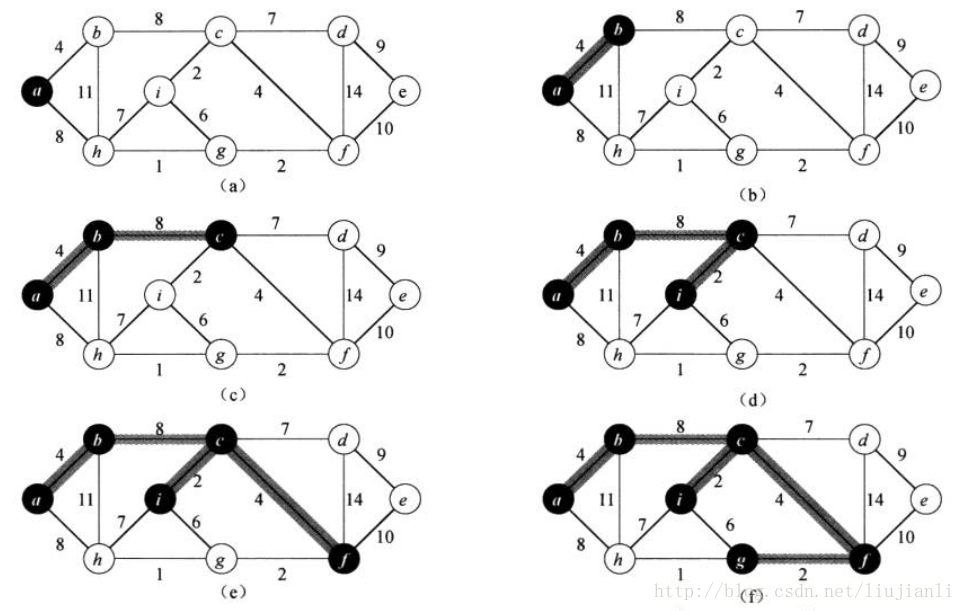
MST-Prim(G, w, r)
    for each u∈G.V
        u.key = ∞
        u.π = NIL
    r.key = 0
    Q = G.V
    while Q != ∅
        u = Extract-Min(Q)
        for each v∈G.Adj[u]
            if v∈Q and w(u,v) < v.key
                v.π = u
                v.key = w(u,v)

Prim算法的时间代价为O(ElgV)。从渐近意义上来说，它与Kruskal算法的运行时间相同。
如果使用斐波那契堆来实现最小优先队列Q，则Prim算法的运行时间将改进到O(E+VlgV)。