并查集的英文是Disjoint Set Union, 因此又称(DSU)
算法导论里的 不相交集合的数据结构 章节指的就是这个。
并查集有两种优化策略:
1.按秩合并 Union by Rank
2.路径压缩 Path Compression
使用与不使用这些策略的时间复杂度分析如下:
在实际应用中,人类现有甚至未来的数据几乎不可能让该算法复杂度过高。 因此可以把该算法复杂度当成近乎线性来使用。
平摊代价指的是在最坏情况下,这些操作的平均复杂度。










 并查集(DSU),全称为Disjoint Set Union,是算法导论中的一种数据结构,用于处理不相交集合。其优化策略包括按秩合并和路径压缩,这两者能有效降低算法复杂度。尽管不使用优化策略时时间复杂度较高,但在实际应用中,由于数据规模限制,可以近似看作线性时间复杂度。平摊代价分析表明,在最坏情况下,这些操作的平均复杂度仍然较低。
并查集(DSU),全称为Disjoint Set Union,是算法导论中的一种数据结构,用于处理不相交集合。其优化策略包括按秩合并和路径压缩,这两者能有效降低算法复杂度。尽管不使用优化策略时时间复杂度较高,但在实际应用中,由于数据规模限制,可以近似看作线性时间复杂度。平摊代价分析表明,在最坏情况下,这些操作的平均复杂度仍然较低。




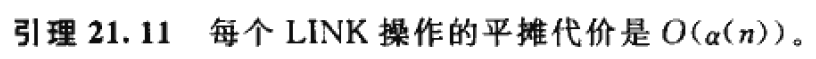
















 469
469

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








