Description
Apurva is obsessed with Fibonacci numbers. She finds Fibonacci numbers very interesting. Fibonacci numbers can be defined as given below.
Fib(1) = 1 , Fib(2) = 1.
Fib(n) = Fib(n-1) + Fib(n-2) for n > 2 .
Given a set S having N elements and an integer K, She wants to find out the value of FIBOSUM(S).
Where sum(s) represents the sum of elements in set s.
Note that values might be repeated in the set, two subsets will be called different if there is an index i such that S[i] is occurring in one of the subset and not in another.
As the value of FIBOSUM(S) can be very large, print it modulo 99991.
Input
First line of input contains two integer N and K sepeated by a space.
Next line contains N space separated integers denoting the set S.
Output
Print a single integer representing the answer.
Constraints
1 ≤ K ≤ N
Subtask #1: 10 points
1 ≤ N ≤ 20, 1 ≤ value in set ≤ 109
Subtask #2: 30 points
1 ≤ N ≤ 2000, 1 ≤ value in set ≤ 109
Subtask #3: 60 points
1 ≤ N ≤ 50000, 1 ≤ value in set ≤ 109
Example
Input:
3 1
1 2 3
Output:
4
Explanation
FIBOSUM(S) = Fib(1) + Fib(2) + Fib(3) = 4.
Solution
-
这题我们可以用到斐波那契数列的通项公式: F n = 1 5 [ ( 1 + 5 2 ) n − ( 1 − 5 2 ) n ] F_n=\frac{1}{\sqrt 5}[(\frac{1+\sqrt 5}{2})^n-(\frac{1-\sqrt 5}{2})^n] Fn=51[(21+5)n−(21−5)n]
-
由于 5 在模数 99991 下有二次剩余(直接枚举出来),设为 P P P。
-
那么我们用 P P P 去替换上式中的 5 \sqrt 5 5 就好算了。
-
令 n = ∑ S i n=\sum S_i n=∑Si ,其中 S i S_i Si 表示集合中不同的 k k k 个数的和,
-
于是我们就可以通过计算 ( 1 + 5 2 ) S i (\frac{1+\sqrt 5}{2})^{S_i} (21+5)Si 和 ( 1 − 5 2 ) S i (\frac{1-\sqrt 5}{2})^{S_i} (21−5)Si 来得到答案了。
-
计算这个我们可以用分治 FFT 来计算(由于99991不是NTT模数,要用任意模数NTT)。
-
比如说做到区间(l,r),而 (l,mid) 和 (mid+1,r) 已经处理好了(即得到两个多项式,次数界为k+1, x i x^i xi 的系数表示有 i i i 个数相乘的和)。
-
那么区间 ( l , r ) (l,r) (l,r) 的多项式就直接由其两个子区间的多项式相乘即可。
-
时间复杂度为 O ( n l o g 2 n ) O(n\ log^2n) O(n log2n) 。
Code
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cctype>
using namespace std;
typedef long long LL;
const int N=50005,mo=99991,p=321;
const double Pi=acos(-1);
int G,n,k,n5,tot1,tot2;
int a[N<<1],b[N<<1],rev[N<<2];
int sa[N],ea[N],sb[N],eb[N];
struct comp
{
double r,i;
comp(){}
comp(double rr,double ii){r=rr,i=ii;}
friend comp operator +(comp x,comp y)
{
return comp(x.r+y.r,x.i+y.i);
}
friend comp operator -(comp x,comp y)
{
return comp(x.r-y.r,x.i-y.i);
}
friend comp operator *(comp x,comp y)
{
return comp(x.r*y.r-x.i*y.i,x.r*y.i+x.i*y.r);
}
};
comp a1[N<<2],a2[N<<2],b1[N<<2],b2[N<<2];
comp c1[N<<2],c2[N<<2],c3[N<<2],w[N<<2];
inline int read()
{
int X=0,w=0; char ch=0;
while(!isdigit(ch)) w|=ch=='-',ch=getchar();
while(isdigit(ch)) X=(X<<1)+(X<<3)+(ch^48),ch=getchar();
return w?-X:X;
}
inline int ksm(int x,int y)
{
int s=1;
while(y)
{
if(y&1) s=(LL)s*x%mo;
x=(LL)x*x%mo;
y>>=1;
}
return s;
}
inline void FFT(comp *y,int len,int ff)
{
for(int i=0;i<len;i++)
if(i<rev[i]) swap(y[i],y[rev[i]]);
for(int h=2;h<=len;h<<=1)
{
int half=h>>1;
for(int i=0;i<half;i++)
{
comp wn=ff>0?w[i*len/h]:w[len-i*len/h];
for(int k=i;k<len;k+=h)
{
comp u=y[k],v=wn*y[k+half];
y[k]=u+v;
y[k+half]=u-v;
}
}
}
if(ff==-1)
for(int i=0;i<len;i++) y[i].r/=len;
}
void solve(int l,int r)
{
if(l==r) return;
int mid=l+r>>1;
solve(l,mid);
solve(mid+1,r);
tot1=0;
for(int i=sa[l];i<=ea[l];i++)
{
a1[tot1]=comp(a[i]/p,0);
b1[tot1++]=comp(a[i]%p,0);
}
tot2=0;
for(int i=sa[mid+1];i<=ea[mid+1];i++)
{
a2[tot2]=comp(a[i]/p,0);
b2[tot2++]=comp(a[i]%p,0);
}
int m=1,ll=0;
while(m<tot1+tot2) m<<=1,ll++;
for(int i=0;i<m;i++) rev[i]=rev[i>>1]>>1|(i&1)<<ll-1;
for(int i=0;i<=m;i++) w[i]=comp(cos(2*Pi*i/m),sin(2*Pi*i/m));
for(int i=tot1;i<m;i++) a1[i]=b1[i]=comp(0,0);
for(int i=tot2;i<m;i++) a2[i]=b2[i]=comp(0,0);
FFT(a1,m,1),FFT(b1,m,1);
FFT(a2,m,1),FFT(b2,m,1);
for(int i=0;i<m;i++)
{
c1[i]=a1[i]*a2[i];
c2[i]=a1[i]*b2[i]+a2[i]*b1[i];
c3[i]=b1[i]*b2[i];
}
FFT(c1,m,-1),FFT(c2,m,-1),FFT(c3,m,-1);
for(int i=0;i<tot1+tot2-1;i++)
{
int num=(LL)(c1[i].r+0.5)*p%mo*p%mo;
num=(num+(LL)(c2[i].r+0.5)*p)%mo;
num=(num+(LL)(c3[i].r+0.5))%mo;
a[sa[l]+i]=(num+mo)%mo;
}
ea[l]=sa[l]+tot1+tot2-2;
tot1=0;
for(int i=sb[l];i<=eb[l];i++)
{
a1[tot1]=comp(b[i]/p,0);
b1[tot1++]=comp(b[i]%p,0);
}
tot2=0;
for(int i=sb[mid+1];i<=eb[mid+1];i++)
{
a2[tot2]=comp(b[i]/p,0);
b2[tot2++]=comp(b[i]%p,0);
}
m=1,ll=0;
while(m<tot1+tot2) m<<=1,ll++;
for(int i=0;i<m;i++) rev[i]=rev[i>>1]>>1|(i&1)<<ll-1;
for(int i=tot1;i<m;i++) a1[i]=b1[i]=comp(0,0);
for(int i=tot2;i<m;i++) a2[i]=b2[i]=comp(0,0);
FFT(a1,m,1),FFT(b1,m,1);
FFT(a2,m,1),FFT(b2,m,1);
for(int i=0;i<m;i++)
{
c1[i]=a1[i]*a2[i];
c2[i]=a1[i]*b2[i]+a2[i]*b1[i];
c3[i]=b1[i]*b2[i];
}
FFT(c1,m,-1),FFT(c2,m,-1),FFT(c3,m,-1);
for(int i=0;i<tot1+tot2-1;i++)
{
int num=(LL)(c1[i].r+0.5)*p%mo*p%mo;
num=(num+(LL)(c2[i].r+0.5)*p)%mo;
num=(num+(LL)(c3[i].r+0.5))%mo;
b[sb[l]+i]=(num+mo)%mo;
}
eb[l]=sb[l]+tot1+tot2-2;
}
int main()
{
for(int i=0;i<mo;i++)
if((LL)i*i%mo==5)
{
n5=i;
break;
}
n=read(),k=read();
int num1=(LL)(1+n5)*ksm(2,mo-2)%mo;
int num2=(LL)(1-n5+mo)*ksm(2,mo-2)%mo;
for(int i=1;i<=n;i++)
{
int x=read();
a[sa[i]=++tot1]=1;
a[ea[i]=++tot1]=ksm(num1,x);
b[sb[i]=++tot2]=1;
b[eb[i]=++tot2]=ksm(num2,x);
}
solve(1,n);
int ans=(LL)(a[k+1]-b[k+1]+mo)*ksm(n5,mo-2)%mo;
printf("%d",ans);
return 0;
}











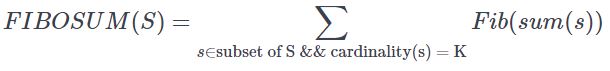














 191
191











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








