仿射变换
- 使用OpenCV函数 warpAffine 来实现一些简单的重映射.
- 使用OpenCV函数 getRotationMatrix2D 来获得一个
 旋转矩阵
旋转矩阵
什么是仿射变换?
-
一个任意的仿射变换都能表示为 乘以一个矩阵 (线性变换) 接着再 加上一个向量 (平移).
-
综上所述, 我们能够用仿射变换来表示:
- 旋转 (线性变换)
- 平移 (向量加)
- 缩放操作 (线性变换)
你现在可以知道, 事实上, 仿射变换代表的是两幅图之间的 关系 .
-
我们通常使用
 矩阵来表示仿射变换.
矩阵来表示仿射变换.
考虑到我们要使用矩阵
 和
和  对二维向量
对二维向量  做变换, 所以也能表示为下列形式:
做变换, 所以也能表示为下列形式: or
or ![T = M \cdot [x, y, 1]^{T}](https://i-blog.csdnimg.cn/blog_migrate/001fe047f04c6276d15c0388fd4328e4.png)

怎样才能求得一个仿射变换?
-
好问题. 我们在上文有提到过仿射变换基本表示的就是两幅图片之间的 联系 . 关于这种联系的信息大致可从以下两种场景获得:
- 我们已知
 和 T 而且我们知道他们是有联系的. 接下来我们的工作就是求出矩阵
和 T 而且我们知道他们是有联系的. 接下来我们的工作就是求出矩阵 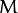
- 我们已知
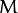 and
and  . 要想求得
. 要想求得 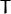 . 我们只要应用算式
. 我们只要应用算式 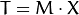 即可. 对于这种联系的信息可以用矩阵
即可. 对于这种联系的信息可以用矩阵 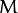 清晰的表达 (即给出明确的2×3矩阵) 或者也可以用两幅图片点之间几何关系来表达.
清晰的表达 (即给出明确的2×3矩阵) 或者也可以用两幅图片点之间几何关系来表达.
- 我们已知
-
让我们形象地说明一下. 因为矩阵
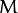 联系着两幅图片, 我们以其表示两图中各三点直接的联系为例. 见下图:
联系着两幅图片, 我们以其表示两图中各三点直接的联系为例. 见下图: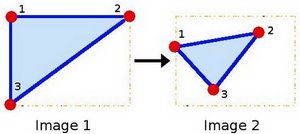
点1, 2 和 3 (在图一中形成一个三角形) 与图二中三个点一一映射, 仍然形成三角形, 但形状已经大大改变. 如果我们能通过这样两组三点求出仿射变换 (你能选择自己喜欢的点), 接下来我们就能把仿射变换应用到图像中所有的点.
函数:
(1)C++:
void
warpAffine
(
InputArray
src
, OutputArray
dst
, InputArray
M
, Size
dsize
, int
flags
=INTER_LINEAR, int
borderMode
=BORDER_CONSTANT, const Scalar&
borderValue
=Scalar()
)
The function warpAffine transforms the source image using the specified matrix:
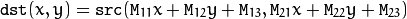
(2)C++: Mat getRotationMatrix2D(Point2f center, double angle, double scale)
计算二维旋转变换矩阵
The function calculates the following matrix:
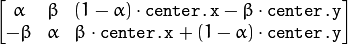
where

官方例程
- 加载一幅图片
- 对这幅图片应用仿射变换. 这个变换是从源图像和目标图像的两组三点之间的联系获得的. 这一步我们使用函数 warpAffine 来实现.
- 仿射变换结束后再对图像应用旋转. 这里的旋转绕图像中点
- 等待用户退出程序



























 510
510

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








