高级管理学：计算题

题1：决策树和期望值

        某企业拟开发新产品，现在有两个可行性方案需要决策。

• 方案一：开发新产品 A，需要追加投资 180 万元，经营期限为 5 年。此间，产品销路好每年可获利 170 万元；销路一般每年可获利 90 万元；销路差每年会亏损 6 万元。三种情况的概率分别为 30%，50%，20%。
• 方案二：开发新产品 B，需要追加投资 60 万元，经营期限为 4 年。此间，产品销路好每年可获利 100 万元；销路一般每年可获利 50 万元；销路差每年可获利 20 万元。三种情况的概率分别为 60%，30%，10%。

（1）画出决策树（6 分）。

（2）计算各点的期望值，并做出最优决策（3 分）。

解1：

 解2：

• 方案一：期望值=170*30%*5+90*50%*5-6*20%*5=474 万元，净收益值 =474-180=294 万元。
• 方案二：期望值=100*60%*4+50*60%*4+20*10%*4=308 万元，，净收益值 =308-60=248 万元。
• 因 294>248,故选方案一。

题二：关键路径

        某工程项目各活动之间关系及平均作业时间如下图所示，绘制网络图，计算时间参数并确定关键路径

活动名称	A	B	C	D	E	F	G	H	I	J	K
先行活动	-	-	-	A	B	B	C	D,E	E,F,G	E,F,G	J
作业时间	18	20	15	24	20	11	13	25	10	20	10

答：

网络图

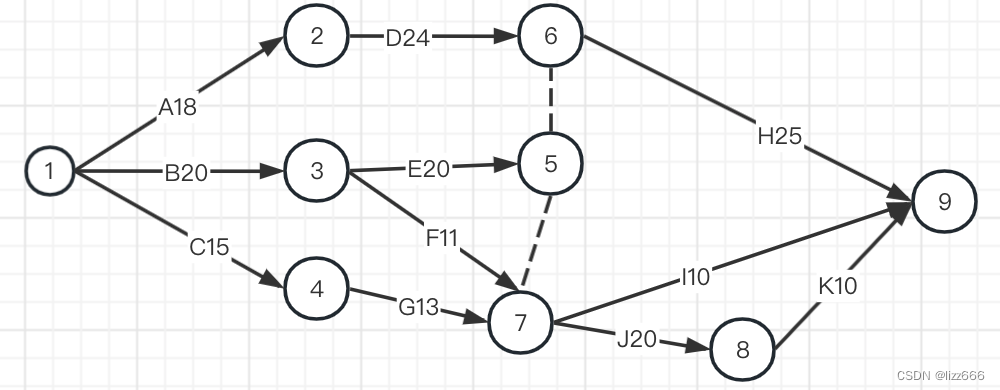
关键路径：画出每条从开始到结束的路径，并计算总作业时长，时间最大的一条为关键路径

1. ADH=18+24+25 = 67
2. BEH = 20 +20 +25 = 65
3. BEI = 20+20+10 =50
4. BEJK=20+20+20+10=70
5. BFI=20+11+10=41
6. BFJK=20+11+20+10=61
7. CGI =15+13+10=38
8. CGJK=15+13+20+10=58

BEJK=70为关键路径

题三：遗憾准则

        某公司准备赴 E、F和 G三个国家进行投资。不同国家的投资环境存在着好、一般
和不好三种不同情形。同样一笔投资，未来五年间在三个不同国家可能产生不同的收益
（如下表)。请你依据遗憾准则帮助该公司选择前往投资的国家。

三个国家的预期收益表，单位：万元

	E	F	G
环境好	9000	7500	8500
环境一般	5000	4000	6000
环境差	3000	1000	3000

 解：

	E	F	G
好	0	1500	500
一般	1000	2000	0
差	0	2000	0
选择	1000	2000	500

后悔遗憾准则：选择与最好结果偏差不大的

• 环境好：时最好收益为9000，E偏差0，F偏差1500，G偏差500
• 环境一般：最好收益为6000,E偏差1000，F偏差2000, G偏差0
• 环境差：最好收益为,3000,E偏差0，E偏差2000，G偏差0
• 选择各国中偏差最大E1000、F2000、G500中最小值
• 选择G国投资 

乐观准则：选择结果最好的

1. 选择最大收益E9000、F7500、G8500中最大值
2. 故选择E国投资

悲观准则：在最坏的结果中选择他们认为最好的行动方案

1. 选择各国中最差收益E3000、F2000、G3000中最大值
2. 故选择E或

等概率准则：选择期望值最大的行动方案(在概率论和统计学中，期望值（或数学期望、或均值，亦简称期望，物理学中称为期待值）是指在一个离散性随机变量试验中每次可能结果的概率乘以其结果的总和。)这里期望值的计算可参照决策树中期望收益值的计算方法。

1. E国期望值 = （9000+5000+3000）/3 = 5667
2. F国期望值 = （7500+4000+1000）/3 = 4167
3. G国期望值 = （8500+6000+3000）/3 = 5834
4. 选择其中最大值，G国