信息系统项目管理师-计算题汇总！大全！

整体管理

1. 净现值分析

把所有预期的未来现金流入和流出都则算成现值，以计算一个项目预期的净货币收益与损失。

现金流*折现因子=净现值。比如现金100元，折现因子0.9，净现值就是90元。

1. 投资收益率分析ROI

将净收入除以投资额所得的值。ROI越大越好。

投资收益率=（总的折现收益-总的折现成本）/则现成本

1. 投资回收期分析

就是以净现金流入补偿净投资所用的时间。越短越好。

动态回收期

下题折现率为10%，求动态回收期，考试中折现率一般都是10%，记住折现因子=（1+折现率）的-1、-2、-3、-4次方，比较难计算，记住折现因子为0.91、0.83、0.75、0.68

现金流是收入和成本的和；净现金流现值是现金流*折现因子；累计净现金流量值是是净现金流量值的总和。

动态投资回收期=3-1+(464/675)=2.68=2.7年

投资回收期= 累计净现金值开始出现正值的那年-1+（前一年的累计净现金值/这一年的净现金流）

进度管理

1. 前导图/紧前关系图

最早结束时间EF=最早开始时间ES+工期

最迟开始时间LS=最迟结束时间LF-工期

最早开始时间	工期	最早完成时间
活动名称
最迟开始时间	总浮动时间	最迟完成时间

1. 箭线图（例题1）

虚线是实际工作中不存在的一中虚设工作，因此通常不占用资源，不消耗时间，表示出来工时为0，它的作用只是为了正确表达工作间的逻辑关系。

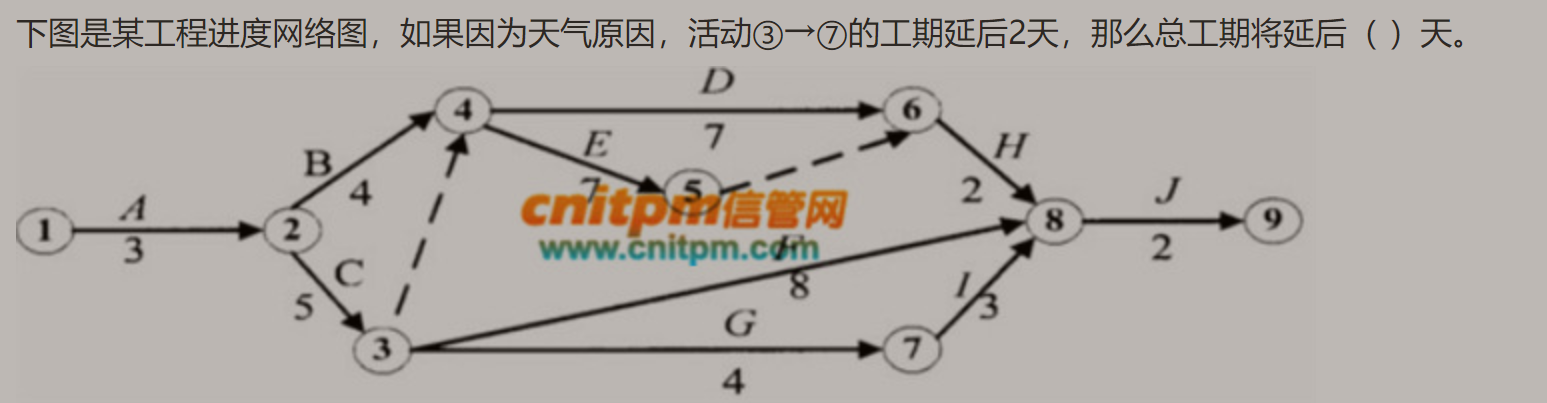
所以此题总工期延后0天。

1. 关键路径法

进度网络图中可能有多条关键路径

关键活动的总浮动时间为0

“自由浮动时间”是指在不延误任何紧后活动的最早开始时间，且不违反进度制约因素的前提下，活动可以从最早开始时间推迟或拖延的时间量。

关键路径是项目中时间最长的活动顺序，决定着可能的项目最短工期。

1. 三点估算PERT（例题3）

乐观时间T1：任何事情都按顺序的情况下，完成某项工作的时间

最可能时间T2：正常情况下，完成某项工作的时间

悲观时间T3：最不利情况下，完成某项工作的时间

期望时间T4：我们期望的时间

期望时间=（乐观时间+4*最可能时间+悲观时间）/6

标准差=（悲观时间-乐观时间）/6

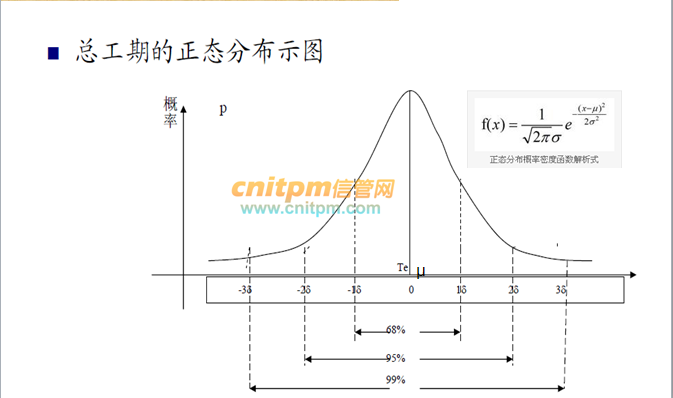
+-1个标准差的面积为68.3%

+-2个标准差的面积为95%

+-3个标准差的面积为95%

在期望时间内完成的概率为50%

例题：

解答：

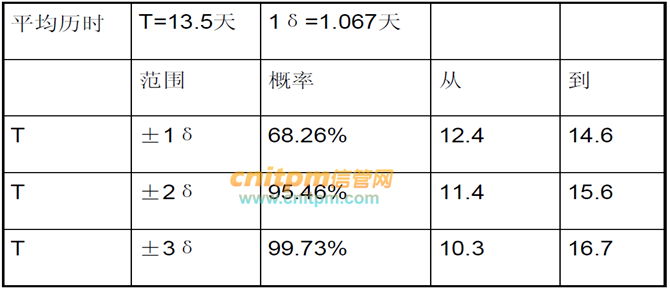
13.5天完成项目的概率为50%

68.26%的一半，34.13%

14.57天内完成的概率是84.13%

例题：

完成某信息系统集成项目中的一个最基本的工作单元A所需的时间，乐观的估计需8天，悲观的估计需38天，最可能的估计需20天，按照PERT方法进行估算，项目的工期应该为 (37) ，在26天以后完成的概率大致为 (38) 。 A．8.9%B．15.9%C．22.2%D．28.6%

答案解析

B

[分析] 期望工期=(8+4×20+38)/6=21 标准差=(38-8)/6=5 26天与21天之间为1个标准差(而非±1个标准差)，16天到26天之间为±1个标准差，根据正态分布规律，故16天到26天之间完成的概率为68.26%，26天以后完成的概率=(1-68.26%)/2=15.87%。

成本管理

1. 项目预算

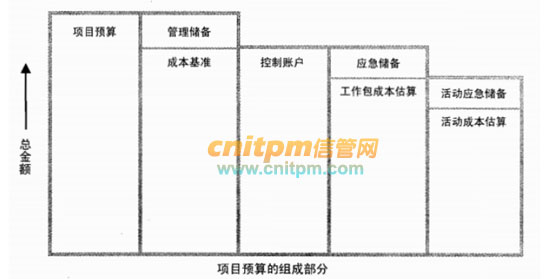
1. 回收期

指投资项目的未来现金净流量与原始投资额相等所经历的时间，既原始投资额通过未来现金流量所回收需要的时间。

累计现金流量开始出现正值的年份数-1+上一年累计现金流的绝对值/出现正值年份的净现金流量

1. 投资回报率

通过投资而应返回的价值，即企业从一项投资活动中得到的经济回报。

1. 内部报酬率IRR

使投资项目的净现值对于零的贴现率

1. 现金流贴现

就是把企业未来特定期间内的预期现金流量还原为当前现值

1. 净现值NPV

是指一个项目预期实现的现金流入的现值与实施该项计划的现金之处的现值的差额

7.三点估算（例题1）

来界定活动成本的近似区间，可以提高活动成本估算的准确性

最可能成本Cm，最乐观成本Co，最悲观成本Cp，常用的计算预期成本Ce的公式：

三角分布Ce=(Co+Cm+Cp)/3

贝塔分布Ce=（Co+4Cm+Cp)/6

例题1：

某项目估算，最乐观成本105万，利用三点估算法，按三角分布计算出的值为94万元，按β分布，计算出的值为94.5万元，则最悲观成本为（）万元。

解答：

信息系统项目管理师教程第3版P281:计划评审技术

三角分布 =（最悲观+最乐观+最可能）÷3，贝塔分布=（最悲观+最乐观+最可能×4）÷6

假设最悲观成本为X，最可能成本为Y，得出下列方程组：

（X+Y+105）/3=94

（X+4Y+105）/3=94.5

得出X=82 Y=95

1. 挣值分析（例题7）

看例题4、5

PV planned value 计划工作的预算价值

EV Earned value 实际完成工作的预算价值

AC Actual Cost 实际完成工作所花费的成本

BAC: Budget at completion 完工预算，就是成本基准=估算成本+应急储备，不要加上管理储备（看例题2）

项目的总计划价值 PV 的总和

当 EV = BAC 时，意味着项目完工

缩写	含义	公式	公式翻译	结果好	结果不好
SV	进度偏差	EV-PV	实际完成工作-计划完成工作	>0，进度提前	<0，进度落后
CV	成本偏差（例7）	EV-AC	计划完成工作成本-实际花费成本	>0，成本节约	<0，成本超支
SPI	进度绩效指数	EV/PV	实际完成工作/计划完成工作	>1，进度超前	<1，进度落后
CPI	成本绩效指数	EV/AC	实际完成工作/实际成本	>1，成本节约	<1，成本超支

完工估算EAC

EAC=ETC完工尚需估算+AC实际成本
典型偏差，如果预期项目剩余部分的CPI 不变	EAC = BAC / CPI（看例题1、2）
非典型偏差，如果未来工作将按计划速度完成 （后续不再发生成本偏差）	EAC = AC + ( BAC - EV )（例题1、2）
如果最初计划不再有效	EAC = AC + 自下而上估算的 ETC
如果CPI和SPI都会影响剩余工作	EAC = AC + （ BAC - EV ）/ （ CPI * SPI ）

完工尚需估算（看例题5）

典型情况（默认）	当前的 CPI 在以后会继续	ETC =（ BAC - EV ）/ CPI
非典型情况	当前 CPI 不再延续，一切回归原计划轨道	ETC = EAC - AC
重新自下而上估算剩余工作	重新自下而上估算剩余工作	ETC = 重新估算

完工尚需绩效指数（大于1都是不好的，小于1都是好的）

TCPI = 剩余工作 / 剩余资金

为完成计划必须保持的效率，则使用：TCPI = ( BAC - EV ) / ( BAC - AC )

为完成当前完工估算必须保 持的效率，则使用：TCPI = ( BAC - EV ) / ( EAC - AC )

TCPI < 1 轻易完成 TCPI > 1 成本超支

例题1：

某项目按工作量平均分配到10个月完成，每月成本相同，项目管理储备15万元。在项目进行到第3个月末时，项目实际花费为BAC的30%，完成总工作量的20%，如果不加以纠偏，根据当前进度，项目完工估算为120万元，则项目总预算为（）万元。

解答：

根据题干可知，管理储备为15万元，PV=0.3BAC，AC=0.3BAC，EV= 0.2BAC，BAC未知，EAC=120万元，CPI=EV/AC=2/3

如果不加以纠偏，属于典型情况，所以 EAC=BAC/CPI=120万元，BAC=120*(2/3)=80

所以，项目总预算=BAC＋管理储备=80万元＋15万元=95万元

例题2：

某项目的估算成本为90万，在此基础上，公司为项目设置10万元的应急储备和10万元的管理储备，项目工期为5个月，项目进行到第三个月的时候，项目SPI为0.6，实际花费为70万元，EV为60万元。以下描述正确的是（）。

A、项目的项目总预算为110万元

B、项目的成本控制到位。进度上略有滞后

C、基于典型偏差计算，到项目完成时，实际花费的成本为100万元

D、基于非典型偏差计算，到项目完成时，实际花费的成本为117万元

解答：

BAC=90+10=100万，总预算=BAC+管理储备。

AC=70万；EV=60万，SPI=0.6=EV/PV，计算出PV=100万

CV成本偏差=EV-AC=-10<0，成本超支

SV进度偏差= EV-PV=-40<0，进度落后

典型偏差EAC=BAC/CPI=100/（60/70）=117

非典型偏差EAC=AC+（BAC-EV）=70+100-60=100

例题3

下表给出了某项目到2019年6月30日为止的成本执行（绩效）数据。如果当前的成本偏差是典型的，下表给出了某项目到2019年6月30日为止的成本执行（绩效）数据。如果当前的成本偏差是典型的，则完工估算（EAC）为：（ ）元。

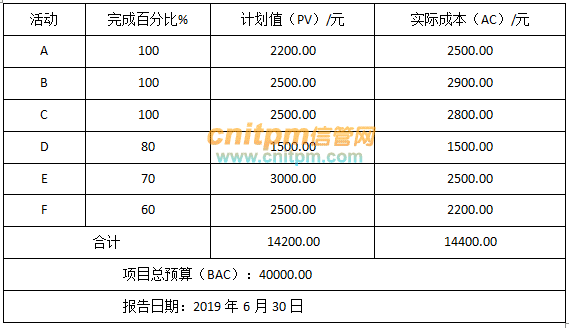
解答：

完成百分比也就是进度指数SPI=EV/PV，还已知的是PV、AC、BAC。

由此可计算出EV，A的EV=2200，B的EV=2500，C的EV=2500，D的EV=0.8*1500=1200，E的EV=0.7*3000=2100，F的EV=0.6*2500=1500。EV总和是12000。

EAC=BAC/CPI=40000/(12000/14400),算出是48000

例题4：

某系统集成项目包含了三个软件模块，现在估算项目成本时，项目经理考虑到其中的模块A技术成熟，已在以前类似项目中多次使用并成功交付，所以项目经理忽略了A的开发成本，只给A预留了5万元，以防意外发生。然后估算了B的成本为50万元，C的成本为30万元，应急储备为10万元，三者集成成本为5万元，并预留了项目的10万元管理储备。如果你是项目组成员，该项目的成本基准是（？）万元，项目预算是（？）万元，项目开始执行后，当项目的进度绩效指数SPI为0.6时，项目实际花费70万元，超出预算10万元，如果不加以纠偏，请根据当前项目进展，估算该项目的完工估算值（EAC）为（？）万元。

解答：

成本基准包括成本+应急储备，但是不包括管理储备。故成本基准=5+50+30+10+5=100、

项目预算=成本基准+管理储备=100+10=110.

由题目可知AC=10，SPI=0.6

此题的关键就在于千万不要认为EV=60万。成本超支10万，故PV=60万！

SPI=EV/PV，EV=SPI*PV=36

CPI=EV/AC=36/70

EAC=BAC/CPI=100/(36/70)=194.4

例题5：

某项目包含A、B、C三项主要活动，项目经理在成本估算时采用自下而上的估算方法，分别估算出三项活动的成本分别为13万元，23万元和8万元，同时为了应对未来可能遇到的不确定因素，预留了10万元的管理储备，同时为每个活动预留了2万元的准备金，该项目的总预算为（ 1 ）万元。项目进行到第二个月时，实际花费为20万元，完成总工作量的30%。如果项目按照当前的绩效继续进行下去，预测项目的完工尚需成本ETC约为（ 2 ）万元

解答：

总预算60万。

那0.3是完成的，EV和PV就都是50*0.3吧

ETC=（BAC-EV）/CPI=(50-50*0.3)/ (50*0.3/20)=46.7万。

例题6：

某大型项目进行到两年时，使用挣值法所需的三个中间变量的数值分别是：计划值PV为400万元，实际成本AC为200万元，挣值EV为100万元。基于该项目的成本偏差，下列描述中正确的是(38)；基于该项目的成本绩效指数，下列描述中正确的是(39)。

(38)A．项目成本偏差为负且项目处于超支状态

B．项目成本偏差为正且项目处于超支状态

C．项目成本偏差为负且项目处于成本节约状态

D．项目成本偏差为正且项目处于成本节约状态

(39)A．成本绩效指数小于l且实际发生的成本是预算成本的2倍

B．成本绩效指数大于1且实际发生的成本是预算成本的一半

C．成本绩效指数小于1且实际发生的成本是预算成本的一半

D．成本绩效指数大于1且实际发生的成本是预算成本的2倍

成本偏差CV=EV-AC=100-200<0，成本超支，选A

成本绩效CPI=EV/AC=100/200=0.5<1，选A

例题7：

干系人管理🆗

1. 沟通渠道计算

（n*（n-1））/2，其中n指参与沟通人数

风险管理🆗

1. 风险概率和影响矩阵

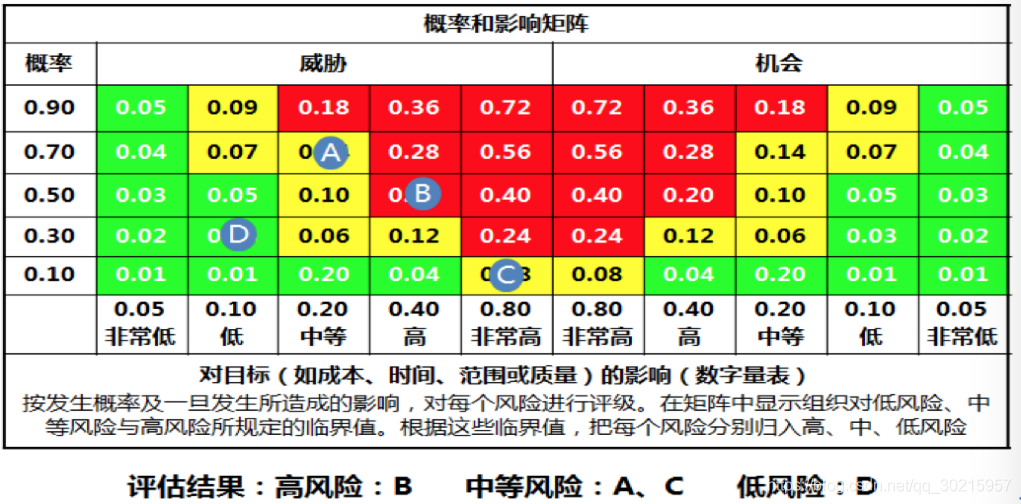
1. 决策树（例题1）

决策树的构成有四个要素：决策结点、方案枝、状态结点、概率枝

某厂房建设或者升级的两种方案的决策树分析如下图所示，由图可知，组织宜选择（ ）的方案，因为该方案的EMV为（ ）万元。

建设新厂房EMV=（200-100)*0.7+(90-100)*0.3=67,升级现有厂房EMV=（120-60）*0.7+（60-60）*0.3=42

应该选建造新厂房，EMV是67

管理科学🆗

1. 最小生成树（例题1）

下图标明了六个城市（A~F）之间的公路（每条公路旁标注了其长度公里数）。为将部分公路改造成高速公路，使各个城市之间均通过高速公路通达，至少要改造共计（）公里的公路，这种总公里数最少的改造方案共有（）个。

解析：

（1）普里姆算法

任取一点，例如A，将其纳入已完成部分。点A与其他各点中的最小距离为AE=200，从而将边AE以及点E纳入已完成部分，点A、E与其他各点B、C、D、F这两个集合之间的最短距离为AF=AB=300，从而可以将边AB与点B（或边AF与点F）纳入已完成部分。

点A、B、E与点C、D、F两个集合的最短距离为AF=BF=300，从而可以将边AF（或边BF）与点F纳入已完成部分。

点A、B、E、F与点C、D两个集合之间的最短距离为FD=200，从而将边FD与点D纳入已完成部分。

点A、B、E、F、D与点C两个集合之间的最短距离为CD=300，从而将边CD与点C纳入已完成部分。

此时，所有6个点都已经接通，其选为AE、AB、AF、FD、CD，总长度为1300。

（2）克鲁斯卡尔算法

依次选取长度最小的边，题干图中是6个结点则需要5条边（边数=结点数-1），因此有：AE、FD为200，AB、BF、AF、CD为300，所以最终方案有3种（连接AE、DF后还要连接三条边，设300米的AB、AF、BF、CD中，去掉任意一条边，再去掉不符合条件的，得出三种）。

1. 最大流量（例题1）

希赛视频教程：

6.2.3. 网络与最大流量问题_哔哩哔哩_bilibili

例题：

下图标出了某地区的运输网。各节点之间的运输能力如下表（万吨/小时），从节点1到节点6的最大运输能力（流量）可以达到（）万吨/小时。

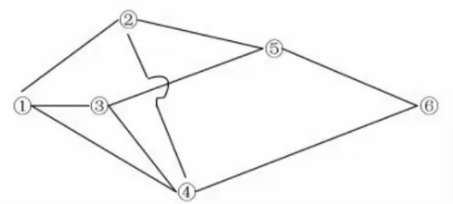
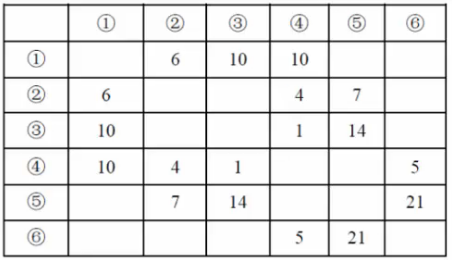
1. 决策论（例题1）注意注意

某公司需要根据下一年宏观经济的增长趋势预测决定投资策略。宏观经济增长趋势有不景气、不变和景气三种，投资策略有积极、稳健和保守三种，各种状态收益如下表。

1、乐观主义准则

乐观主义准则，也称为"最大最大准则"，其决策原则是"大中取大"。决策者依次在决策表中的各个投资方案所对应的各个结果中选择出最大结果，并记录，最后再从这些结果中选出最大者，其所对应的方案是应该采取的决策方案。

在本题中，积极方案的最大结果是500，稳健方案最大结果是300，保守方案最大结果是,400，三者最大值是500，选择其对应的积极投资方案。

2、悲观主义准则

悲观主义准则也称为"最大最小"原则，其决策原则是"小中取大"。决策者依次在决策表中各个投资方案所对应的各个结果中选出最小结果，并记录，最后再从这些结果中选出最大者，其所对应的方案就是应该采取的方案。

例如本题，积极方案中最小结果是50，稳健方案最小结果是150，保守方案最小结果是200，三者的最大值是200，因此，选择对应的保守投资方案。

3、后悔值准则

后悔值也叫做"最小最大后悔值"，该决策法的基本原理是，将每种自然状态的最高值（指收益矩阵，如果是损失矩阵应取最低值）定为该状态的理想目标，将该状态中的其他值与最高值相比所得之差作为未达到理想的后悔值。为了提高决策的可靠性，在每一方案中选取最大的后悔值，再各方案的最大后悔值中选取最小值作为决策依据，与该值所对应的方案即为入选方案。

乐观：最大最大，选取每种方案中最大的，再取出一个方案中最大的。

悲观：小中取大，选取每种方案中最小的，再取出一个方案中最大的。

后悔值：先计算后悔值，大中取小，先依据每种环境或情况中最赚钱的-现在的（绝对值），在每种方案中选取后悔值（绝对值）最大的，再从中选取后悔值（绝对值）最小的

后悔值矩阵。

在表中，积极方案的最大后悔值为350，稳健方案的最大后悔值为250，保守方案的最大后悔值300。三者中的最小后悔值为250，因此，选择其所对应的稳健投资方案。

例题：

1. 灵敏度分析（例题1）

假设有外表完全相同的木盒100只，将其分为2组，一组装白球，有70盒；另一组装黑球，有30盒。现在这100盒中任取一盒，请你猜，如果这盒内装白球，猜对了得500分，猜错了罚200分；如果这盒内装黑球，猜对了得1000分，猜错了罚150分。为使期望得分最多，应选哪一个方案？

解析：先画出决策树。

猜白球得分：0.7*500-0.3*200=290

猜黑球得分：0.3*1000-0.7*150=195

选择猜白球。

但是当白球的概率从0.7变为0.6时，"猜白"的期望值是220，"猜黑"的期望值是310，此时，"猜黑"变成最优方案。概率的变化引起了最优方案的改变，这个转折点的确定可以采用下面的公式。

设P为出现白球的概率，1-P为出现黑球的概率。当两个方案的期望值相等时，即：

P*500+(1-P)*(-200)=P*(-150)+(1-P)*1000，解出P=0.65（算到小数点后3位，进一位），称之为转折率。

1. 线性规划（例题1）

高项第8章管理科学基础03线性规划_哔哩哔哩_bilibili

线性规划最常考的是列方程求解的问题

解答：

1. 动态规划（例题2）

动态规划是决策分析中的一种常用方法，是解决多阶段决策过程问题的一种最优解化方法。

将问题分成相互联系的阶段，每个阶段都做出决策，从而使整个过程达到最优化

一个标准的动态规划算法包括划分阶段和选择状态两个步骤

例题1：

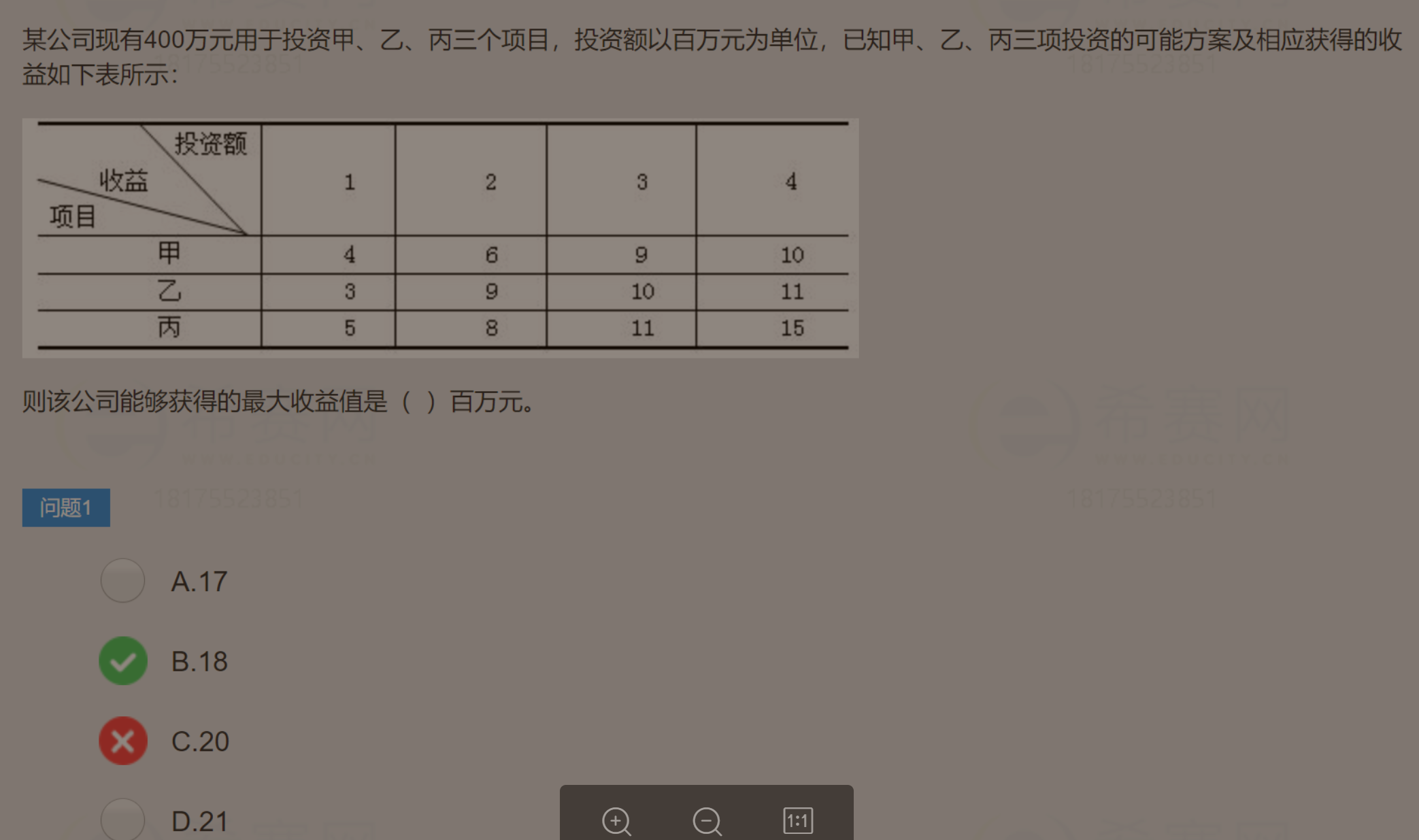
这里注意4.5要*2

例题2：