简介

上述问题就是最小支撑树的应用。我们可以把七个村庄抽象成图像中的7个顶点,图像之间用边来表示,村庄之间的距离通过权重进行表示。那么应该如何求出把七个村庄连接起来的最小边集合呢?
普利姆算法的思想
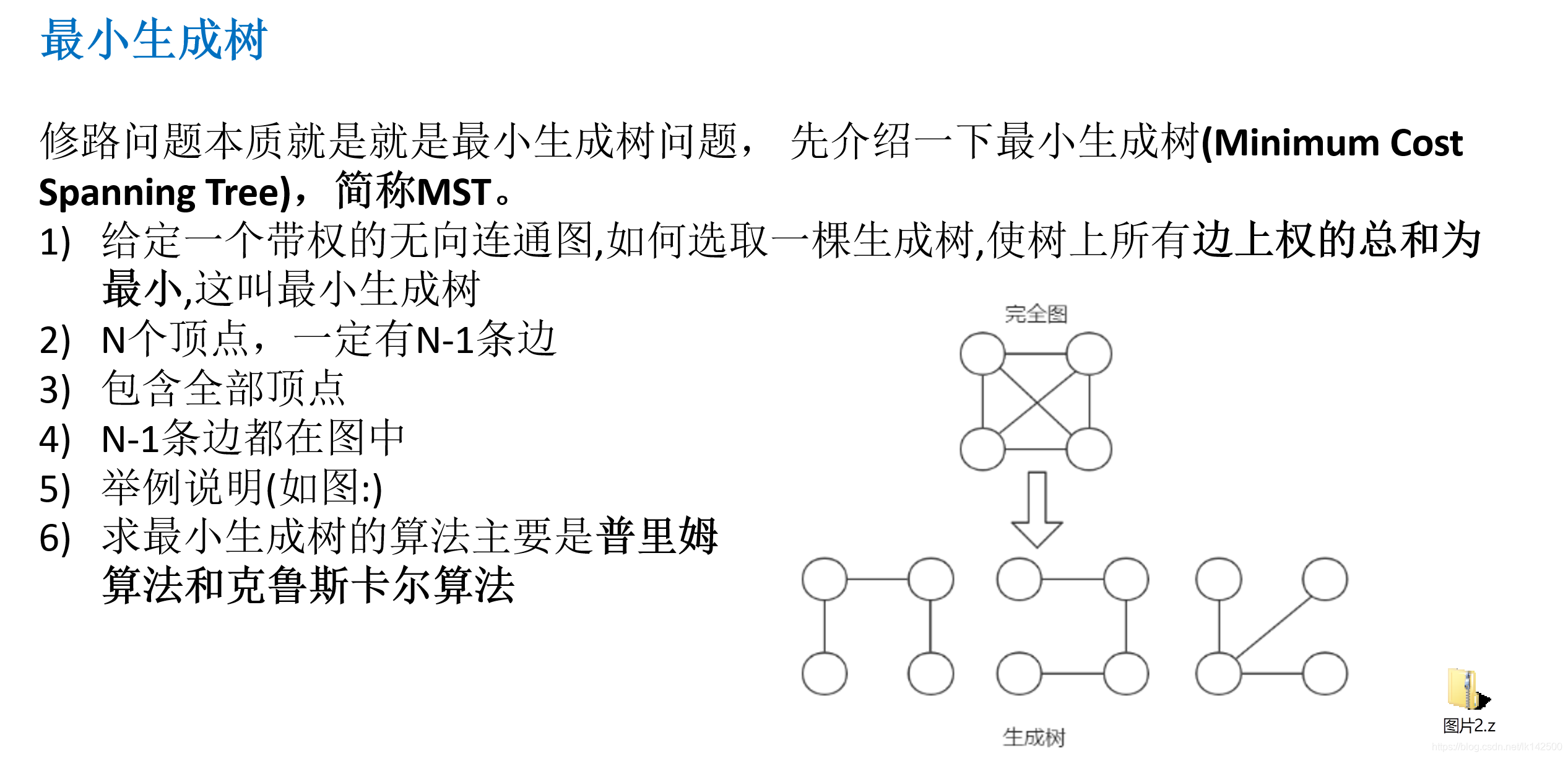
若要在n个顶点之间建立连通图,则至少要n-1个顶点。将这n-1条边上的权重之和定义为连通图的代价。对于一个无向网络----无向加权连通图N=(V, E, C),其顶点个数|V|=n,图中边的个数为|E|,可以从它的|E|条边中选出n-1条边,使之满足:
- 这n-1条边和图的n个顶点构成一个连通图(1)
- 该连通图是所有满足条件(1)而且具有最小代价的连通图。
这样的连通图被称为网络N的最小支撑树(MST)。显然,一个网络可能存在不止一棵最小支撑树
普利姆算法的处理过程如下所示:

从上面的叙述中,我们可以看到,普利姆算法以顶点为核心,因此普利姆算法的算法复杂度为O(n2)
普利姆算法实现

使用两层for循环实现普利姆算法
从上面的论述,我们可以看到,要把顶点分成两个类型:一个已经访问的顶点集合U,一个未访问的顶点集合V-U
在实际运行时,可以通过建立一个visited数组,用true和false来分类两个集合中的顶点。
核心代码如下所示:
/**
* 通过普利姆算法获取图形的最小支撑树
*
* @param vertex 普利姆算法的起始顶点
* @return 返回当前图形的最小支撑树,注意:这要求当前图形是连通图
*/
public MinTree prim(int vertex) {
boolean[] visited = new boolean[numberOfVertex];
Arrays.fill(visited, false);
// 表示vertex结点已经加入最小支撑树
visited[vertex] = true;
MinTree minTree = new MinTree(numberOfVertex);
// 感觉这个过程还是不太好理解。
// 注意选择排序的运用
while (minTree.numberOfMstEdge() < numberOfVertex - 1) {
MSTEdge edge = getShortestEdge(visited);
minTree.addMstEdge(edge);
visited[edge.getEnd()] = true;
}
return minTree;
}
/**
* 获取已访问顶点和未访问顶点之间相连的最短边
* @param visited 辅助遍历数组
* @return 获取最短边,一端是已经访问的点,一端是未访问的顶点。通过遍历求出最短的边
*/
private MSTEdge getShortestEdge(boolean[] visited) {
int minWeight = Integer.MAX_VALUE;
int minStart = Integer.MAX_VALUE;
int minEnd = Integer.MAX_VALUE;
// i 表示已经访问过的集合中的顶点
for (int i = 0; i < numberOfVertex; i++) {
// 表示未访问的顶点集合中的顶点
for (int j = 0; j < numberOfVertex; j++) {
if (visited[i] && !visited[j] && edges[i][j] < minWeight) {
minWeight = edges[i][j];
minStart = i;
minEnd = j;
}
}
}
return new MSTEdge(minStart, minEnd, minWeight);
}
class MinTree {
ArrayList<MSTEdge> mstEdges;
public MinTree(int numberOfVertex) {
mstEdges = new ArrayList<>(numberOfVertex - 1);
}
public void show() {
System.out.println("MinTree.show");
System.out.println("最小支撑树如下所示:");
mstEdges.stream()
.forEach(System.out::println);
}
public void addMstEdge(MSTEdge mstEdge) {
mstEdges.add(mstEdge);
}
public int numberOfMstEdge() {
return mstEdges.size();
}
}
class MSTEdge {
int start;
int end;
int weight;
public MSTEdge(int start, int end, int weight) {
this.start = start;
this.end = end;
this.weight = weight;
}
@Override
public String toString() {
return "MSTEdge{" +
"start=" + start +
", end=" + end +
", weight=" + weight +
'}';
}
public int getEnd() {
return end;
}
}
在此梳理一下:
对于ABCDEFG,七个点,假如说在某个时刻已经确定U = {A B C D}, V-U = {E F G },那么下一个时刻,要添加从{E F G}中选取一个点,因此可以先遍历E-A、 E-B E-C E-D F-A F-B F-C F-D G-A G-B G-C G-D这些,而这恰恰是循环所能做的。因此在上述的代码中getShortestEdge函数正好使用了二层循环,一层循环处理U集合,第二层循环处理V-U集合。然后把获取的最短边添加到最小支撑树中。
使用closedge数组实现普利姆算法
在刘大有《数据结构第二版》的第163页,我们可以看到大有哥也提供了一种计算普利姆算法的实现方式,并且给出了ADL描述。其实两种算法的思路基本上是一致的,不过在实现时,closedge的实现更加灵巧,采用了是累计更新的方式来获取未访问顶点集合到已访问顶点集合的最短边,而上述的使用两层for循环,则是更加的暴力,每次在添加了一条边之后,重头开始进行最短边的计算。
对于普利姆算法的理解如下图所示:
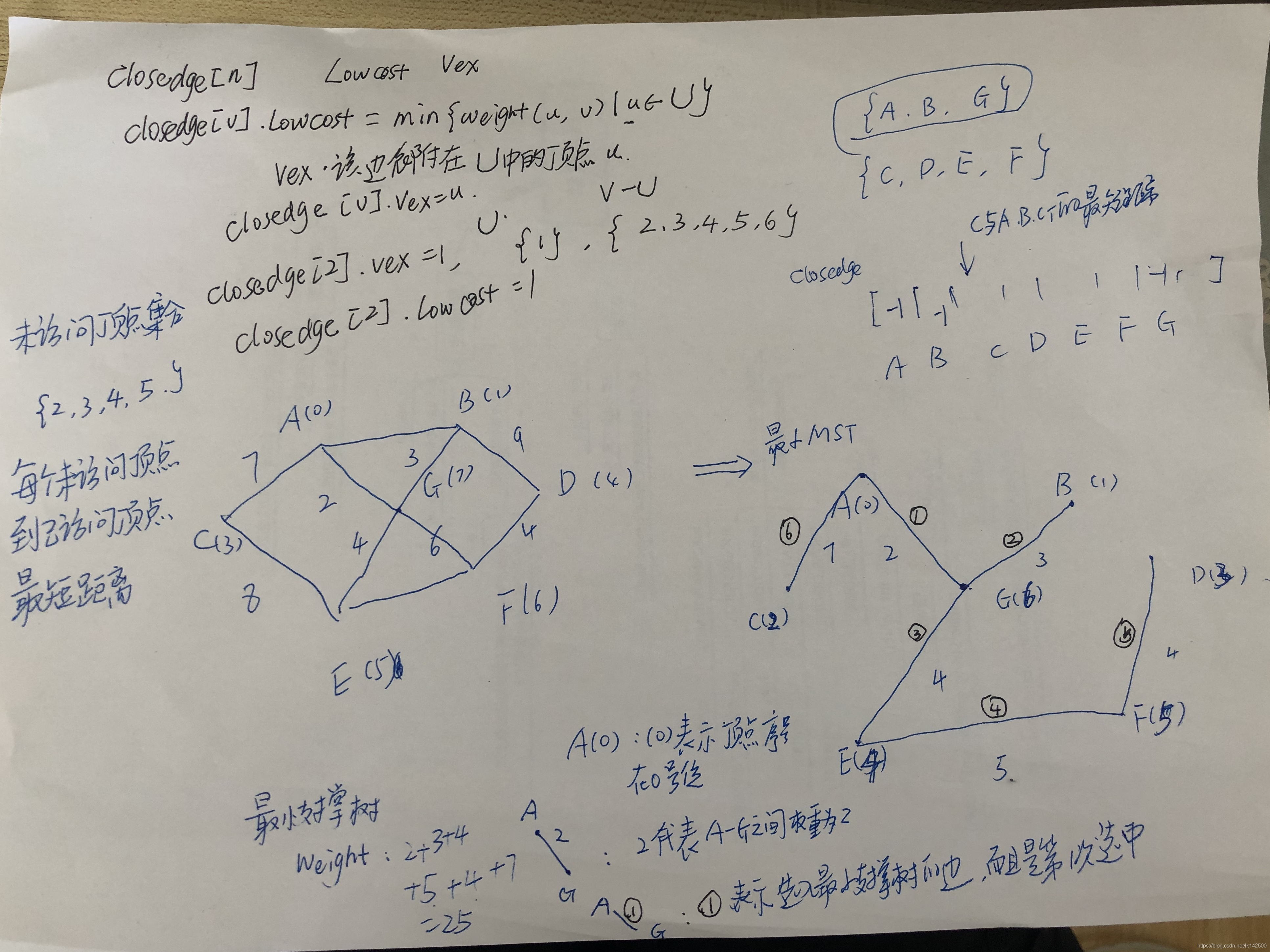
普利姆算法代码实现如下:
/**
* @param vertex 通过普利姆算法获取最小支撑树的开始顶点
* @return 获取最小支撑树
*/
public MinTree prim(int vertex) {
MinTree minTree = new MinTree(numberOfVertex);
// 1. 初始化邻接矩阵 ,当图已经得到良好的初始化了之后,邻接矩阵未初始化的边默认未0
for (int i = 0; i < numberOfVertex; i++) {
for (int j = 0; j < numberOfVertex; j++) {
if (edges[i][j] == 0) {
edges[i][j] = Integer.MAX_VALUE;
}
}
}
show();
// 2. 初始化closedge数组, 以顶点vertex未初始顶点,初始化数组closedge
MinEdge[] closedge = new MinEdge[numberOfVertex];
for (int i = 0; i < numberOfVertex; i++) {
// 设置了每个顶点到已访问顶点vertex的距离
closedge[i] = new MinEdge(vertex, edges[i][vertex]);
}
closedge[vertex].setVertex(-1);
closedge[vertex].setLowcost(0);
// 3. 构造图的最小支撑树
// 循环n-1次,获取n-1条最小的边
for (int i = 0; i < numberOfVertex - 1; i++) {
int minCost = Integer.MAX_VALUE;
// 未访问的目标顶点索引,其与lowcost[unAccessedTargetVertexIndex].getVertex()构成了未访问顶点集合到已访问顶点集合的最短边
int unAccessedTargetVertexIndex = -1;
for (int j = 0; j < numberOfVertex; j++) {
// 采用选择排序获取未访问顶点到已访问顶点的最小值。第一次循环是找出各个顶点到vertex顶点的距离的最小值
if (closedge[j].getVertex() != -1 && closedge[j].getLowcost() < minCost) {
minCost = closedge[j].getLowcost();
// 寻找最短边的位置序号,不断更新直到找到一个最小的。
unAccessedTargetVertexIndex = j;
}
}
// 如果在执行了通过选择排序查找未访问顶点集合到已访问顶点集合的最短边和顶点信息之后,查找的unAccessedTargetVertexIndex为-1表示未查找到有效的顶点
assert unAccessedTargetVertexIndex != -1;
MSTEdge edge = new MSTEdge(unAccessedTargetVertexIndex, closedge[unAccessedTargetVertexIndex].getVertex(), minCost);
minTree.addMstEdge(edge);
// 把找到的未访问顶点标记为已经访问
closedge[unAccessedTargetVertexIndex].setVertex(-1);
closedge[unAccessedTargetVertexIndex].setLowcost(0);
for (int j = 0; j < numberOfVertex; j++) {
// j代表未访问顶点, unAccessedTargetVertexIndex代表已经访问的新的顶点。
// 主要是为了更新,最新的顶点加入到已经访问的集合对未访问的顶点集合的影响。
// 采用选择排序获取未访问顶点到已访问顶点的最小值。第一次循环是找出各个顶点到vertex顶点的距离的最小值
if (closedge[j].getVertex() != -1 && edges[j][unAccessedTargetVertexIndex] < closedge[j].getLowcost()) {
closedge[j].setLowcost(edges[j][unAccessedTargetVertexIndex]);
closedge[j].setVertex(unAccessedTargetVertexIndex);
}
}
}
return minTree;
}
在使用closedge来获得最小支撑树的过程中,使用了如下的结构:
该结构存储了最短路径,也就是closedge数组中每个元素的结构。数组序号表示未访问的顶点序号,vertex表示的是已经访问的顶点序号,lowcost则表示未访问顶点到已经访问顶点的最短距离。
/**
* 刘大有 普利姆算法实现
*/
class MinEdge {
/**
* vertex顶点,含义是已访问的顶点序号
*/
private int vertex;
/**
* 某个未访问顶点到vertex顶点所需要的最短的开销
*/
private int lowcost;
public int getVertex() {
return vertex;
}
public void setVertex(int vertex) {
this.vertex = vertex;
}
public int getLowcost() {
return lowcost;
}
public void setLowcost(int lowcost) {
this.lowcost = lowcost;
}
public MinEdge(int vertex, int lowcost) {
this.vertex = vertex;
this.lowcost = lowcost;
}
}
其中closedge[n]的每个数组元素由lowcost和vertex两个域组成,其定义如下:
- 如果v不属于已访问集合U,则
- closedge[v].lowcost=min{weight(u, v)| u∈U}
- closedge[v].vertex存储的是该边依附在U中的顶点u。
- 如果v∈U,则
- closedge[v].lowcost=0
- closedge[v].vertex=-1 表示该顶点已经访问过了。
closedge数组中的i号元素的含义,i号顶点有没有访问过,由closedge[i].vertex是否等于-1可以进行判断
如果i号顶点未访问,那么closedge[i].vertex表示在集合U中,vertex顶点与i号顶点组成的边是最短权重的边。
可以粗浅的理解:
closedge数组记录了每个未访问顶点到已经访问顶点集合中的最短距离
/**
* 该数组的元素个数与图中的顶点个数相同。
* 数组的元素表示的是未访问的顶点序号
* edges[i] edges[i].lowcost表示当前情况下i号顶点尚未被访问,
* 而距离已访问顶点集合中最近的点未edges[i].vertex,
* edges[i].lowcost表示未访问的顶点i距离已访问的顶点edges[i].vertex之间的距离
*/
MinEdge[] edges;
两种算法比较

具体参见代码
从下述的代码中看,两层for循环与外边的n-1条边组成了三层for循环,性能会差于closedge的实现。
两层for循环
/**
* 获取已访问顶点和未访问顶点之间相连的最短边
* @param visited 辅助遍历数组
* @return 获取最短边,一端是已经访问的点,一端是未访问的顶点。通过遍历求出最短的边
*/
private MSTEdge getShortestEdge(boolean[] visited) {
int minWeight = Integer.MAX_VALUE;
int minStart = Integer.MAX_VALUE;
int minEnd = Integer.MAX_VALUE;
// i 表示已经访问过的集合中的顶点
for (int i = 0; i < numberOfVertex; i++) {
// 表示未访问的顶点集合中的顶点
for (int j = 0; j < numberOfVertex; j++) {
if (visited[i] && !visited[j] && edges[i][j] < minWeight) {
minWeight = edges[i][j];
minStart = i;
minEnd = j;
}
}
}
return new MSTEdge(minStart, minEnd, minWeight);
}
closedge数组
int minCost = Integer.MAX_VALUE;
// 未访问的目标顶点索引,其与lowcost[unAccessedTargetVertexIndex].getVertex()构成了未访问顶点集合到已访问顶点集合的最短边
int unAccessedTargetVertexIndex = -1;
for (int j = 0; j < numberOfVertex; j++) {
// 采用选择排序获取未访问顶点到已访问顶点的最小值。第一次循环是找出各个顶点到vertex顶点的距离的最小值
if (closedge[j].getVertex() != -1 && closedge[j].getLowcost() < minCost) {
minCost = closedge[j].getLowcost();
// 寻找最短边的位置序号,不断更新直到找到一个最小的。
unAccessedTargetVertexIndex = j;
}
}
// 如果在执行了通过选择排序查找未访问顶点集合到已访问顶点集合的最短边和顶点信息之后,查找的unAccessedTargetVertexIndex为-1表示未查找到有效的顶点
assert unAccessedTargetVertexIndex != -1;
MSTEdge edge = new MSTEdge(unAccessedTargetVertexIndex, closedge[unAccessedTargetVertexIndex].getVertex(), minCost);
minTree.addMstEdge(edge);
// 把找到的未访问顶点标记为已经访问
closedge[unAccessedTargetVertexIndex].setVertex(-1);
closedge[unAccessedTargetVertexIndex].setLowcost(0);
for (int j = 0; j < numberOfVertex; j++) {
// j代表未访问顶点, unAccessedTargetVertexIndex代表已经访问的新的顶点。
// 主要是为了更新,最新的顶点加入到已经访问的集合对未访问的顶点集合的影响。
// 采用选择排序获取未访问顶点到已访问顶点的最小值。第一次循环是找出各个顶点到vertex顶点的距离的最小值
if (closedge[j].getVertex() != -1 && edges[j][unAccessedTargetVertexIndex] < closedge[j].getLowcost()) {
closedge[j].setLowcost(edges[j][unAccessedTargetVertexIndex]);
closedge[j].setVertex(unAccessedTargetVertexIndex);
}
}
表示顶点已经被访问
这个在两个算法中,都是存在的,一个是通过visited数组来明确的标记,一个则是通过closedge数组来标记
- visited[i]=true,表示i号顶点已经被访问过
- closedge[i].vertex=-1,表示i号顶点已经访问过,
访问过的含义就是已经加入了已访问顶点集合U。
完整代码实现
package com.atguigu.graph.graph;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.LinkedList;
/**
* 使用邻接矩阵实现图类
*
* @author songquanheng
* @Time: 2020/6/20-11:32
*/
public class Graph {
/**
* 顶点数组
*/
private String[] vertexs;
private int numberOfVertex;
/**
* 边数
*/
private int numberOfEdges;
/**
* 边集合,采用二维数组表示
*/
private int[][] edges;
public static void main(String[] args) {
String[] vertices = "A B C D E F G".split(" ");
Graph graph = new Graph(vertices);
graph.show();
graph.insertEdge(0, 1, 5);
graph.insertEdge(0, 2, 7);
graph.insertEdge(0, 6, 2);
graph.insertEdge(1, 6, 3);
graph.insertEdge(1, 3, 9);
graph.insertEdge(2, 4, 8);
graph.insertEdge(3, 5, 4);
graph.insertEdge(4, 5, 5);
graph.insertEdge(4, 6, 4);
graph.insertEdge(5, 6, 6);
graph.show();
graph.dfs();
System.out.println();
graph.dfs(2);
System.out.println();
graph.bfs();
System.out.println();
graph.bfs(2);
System.out.println();
MinTree minTree = graph.prim(0);
minTree.show();
System.out.println("minTree.getMinWeight() = " + minTree.getMinWeight());
MinTree minTree2 = graph.prim2(0);
minTree.show();
System.out.println("minTree2.getMinWeight() = " + minTree2.getMinWeight());
}
/**
* @param vertex 通过普利姆算法获取最小支撑树的开始顶点
* @return 获取最小支撑树
*/
public MinTree prim(int vertex) {
MinTree minTree = new MinTree(numberOfVertex);
// 1. 初始化邻接矩阵 ,当图已经得到良好的初始化了之后,邻接矩阵未初始化的边默认未0
for (int i = 0; i < numberOfVertex; i++) {
for (int j = 0; j < numberOfVertex; j++) {
if (edges[i][j] == 0) {
edges[i][j] = Integer.MAX_VALUE;
}
}
}
show();
// 2. 初始化closedge数组, 以顶点vertex未初始顶点,初始化数组closedge
MinEdge[] closedge = new MinEdge[numberOfVertex];
for (int i = 0; i < numberOfVertex; i++) {
// 设置了每个顶点到已访问顶点vertex的距离
closedge[i] = new MinEdge(vertex, edges[i][vertex]);
}
closedge[vertex].setVertex(-1);
closedge[vertex].setLowcost(0);
// 3. 构造图的最小支撑树
// 循环n-1次,获取n-1条最小的边
for (int i = 0; i < numberOfVertex - 1; i++) {
int minCost = Integer.MAX_VALUE;
// 未访问的目标顶点索引,其与lowcost[unAccessedTargetVertexIndex].getVertex()构成了未访问顶点集合到已访问顶点集合的最短边
int unAccessedTargetVertexIndex = -1;
for (int j = 0; j < numberOfVertex; j++) {
// 采用选择排序获取未访问顶点到已访问顶点的最小值。第一次循环是找出各个顶点到vertex顶点的距离的最小值
if (closedge[j].getVertex() != -1 && closedge[j].getLowcost() < minCost) {
minCost = closedge[j].getLowcost();
// 寻找最短边的位置序号,不断更新直到找到一个最小的。
unAccessedTargetVertexIndex = j;
}
}
// 如果在执行了通过选择排序查找未访问顶点集合到已访问顶点集合的最短边和顶点信息之后,查找的unAccessedTargetVertexIndex为-1表示未查找到有效的顶点
assert unAccessedTargetVertexIndex != -1;
MSTEdge edge = new MSTEdge(unAccessedTargetVertexIndex, closedge[unAccessedTargetVertexIndex].getVertex(), minCost);
minTree.addMstEdge(edge);
// 把找到的未访问顶点标记为已经访问
closedge[unAccessedTargetVertexIndex].setVertex(-1);
closedge[unAccessedTargetVertexIndex].setLowcost(0);
for (int j = 0; j < numberOfVertex; j++) {
// j代表未访问顶点, unAccessedTargetVertexIndex代表已经访问的新的顶点。
// 主要是为了更新,最新的顶点加入到已经访问的集合对未访问的顶点集合的影响。
// 采用选择排序获取未访问顶点到已访问顶点的最小值。第一次循环是找出各个顶点到vertex顶点的距离的最小值
if (closedge[j].getVertex() != -1 && edges[j][unAccessedTargetVertexIndex] < closedge[j].getLowcost()) {
closedge[j].setLowcost(edges[j][unAccessedTargetVertexIndex]);
closedge[j].setVertex(unAccessedTargetVertexIndex);
}
}
}
return minTree;
}
/**
* 通过普利姆算法获取图形的最小支撑树
*
* @param vertex 普利姆算法的起始顶点
* @return 返回当前图形的最小支撑树,注意:这要求当前图形是连通图
*/
public MinTree prim2(int vertex) {
boolean[] visited = new boolean[numberOfVertex];
Arrays.fill(visited, false);
// 表示vertex结点已经加入最小支撑树
visited[vertex] = true;
MinTree minTree = new MinTree(numberOfVertex);
// 感觉这个过程还是不太好理解。
// 注意选择排序的运用
while (minTree.numberOfMstEdge() < numberOfVertex - 1) {
MSTEdge edge = getShortestEdge(visited);
minTree.addMstEdge(edge);
visited[edge.getEnd()] = true;
}
return minTree;
}
/**
* 获取已访问顶点和未访问顶点之间相连的最短边
* @param visited 辅助遍历数组
* @return 获取最短边,一端是已经访问的点,一端是未访问的顶点。通过遍历求出最短的边
*/
private MSTEdge getShortestEdge(boolean[] visited) {
int minWeight = Integer.MAX_VALUE;
int minStart = Integer.MAX_VALUE;
int minEnd = Integer.MAX_VALUE;
// i 表示已经访问过的集合中的顶点
for (int i = 0; i < numberOfVertex; i++) {
// 表示未访问的顶点集合中的顶点
for (int j = 0; j < numberOfVertex; j++) {
if (visited[i] && !visited[j] && edges[i][j] < minWeight) {
minWeight = edges[i][j];
minStart = i;
minEnd = j;
}
}
}
return new MSTEdge(minStart, minEnd, minWeight);
}
public Graph(String[] vertexs) {
numberOfVertex = vertexs.length;
this.vertexs = new String[numberOfVertex];
int i = 0;
for (String item : vertexs) {
this.vertexs[i++] = item;
}
// 初始化邻接矩阵
this.edges = new int[numberOfVertex][numberOfVertex];
}
public void show() {
System.out.println("Graph.show");
System.out.println(Arrays.toString(vertexs));
System.out.println();
for (int[] row : edges) {
System.out.println(Arrays.toString(row));
}
System.out.println("graph.getNumberOfEdges() = " + getNumberOfEdges());
System.out.println("graph.getNumberOfVertex() = " + getNumberOfVertex());
System.out.println();
}
/**
* @param v1 边的起点的序号
* @param v2 边的终点的序号
* @param w 边的权值 无向图赋值为1即可
*/
public void insertEdge(int v1, int v2, int w) {
assert v1 != v2;
edges[v1][v2] = w;
edges[v2][v1] = w;
numberOfEdges++;
}
/**
* 深度优先遍历,此时不考虑起始点,即以0号序列的顶点为起始顶点
*/
public void dfs() {
System.out.println("Graph.dfs");
boolean[] visited = new boolean[numberOfVertex];
Arrays.fill(visited, false);
for (int i = 0; i < numberOfVertex; i++) {
if (!visited[i]) {
dfs(i, visited);
}
}
System.out.println();
}
/**
* 从指定顶点进行深度优先遍历
*
* @param vertex 开始顶点的序号
*/
public void dfs(int vertex) {
boolean[] visited = new boolean[numberOfVertex];
Arrays.fill(visited, false);
dfs(vertex, visited);
System.out.println();
}
/**
* @param vertex 深度优先遍历的开始顶点所在的序号
*/
private void dfs(int vertex, boolean[] visited) {
System.out.print(vertexs[vertex] + "->");
visited[vertex] = true;
int w = getFirstNeighbour(vertex);
while (w != -1) {
if (!visited[w]) {
dfs(w, visited);
} else {
// 如果w已经被访问过,则访问w的下一个邻接顶点
w = getNextNeighbour(vertex, w);
}
}
}
/**
* 广度优先遍历
*/
public void bfs() {
System.out.println("Graph.bfs");
boolean[] visited = new boolean[numberOfVertex];
Arrays.fill(visited, false);
for (int i = 0; i < numberOfVertex; i++) {
if (!visited[i]) {
bfs(i, visited);
}
}
}
/**
* 从指定顶点vertex开始进行广度优先遍历
*
* @param vertex 从vertex顶点开始进行广度优先遍历
*/
public void bfs(int vertex) {
boolean[] visited = new boolean[numberOfVertex];
Arrays.fill(visited, false);
bfs(vertex, visited);
}
/**
* 从顶点vertex开始进行广度优先遍历
*
* @param vertex 顶点序号
* @param visited 辅助遍历数组
*/
private void bfs(int vertex, boolean[] visited) {
System.out.print(vertexs[vertex] + "->");
visited[vertex] = true;
LinkedList<Integer> queue = new LinkedList<>();
queue.addLast(vertex);
while (!queue.isEmpty()) {
// 此时head所在的顶点已经访问过了
int head = queue.remove();
int w = getFirstNeighbour(head);
while (w != -1) {
if (!visited[w]) {
// 深度优先遍历从此处开始递归,但广度优先不进行递归
System.out.print(vertexs[w] + "->");
visited[w] = true;
queue.addLast(w);
}
w = getNextNeighbour(head, w);
}
}
}
/**
* 返回序号为vertex的第一个邻接顶点的序号
*
* @param vertex 顶点的序号,对于A顶点,则传入的vertex为A顶点所在的序号0
* @return 返回该顶点的第一个邻接顶点所在的序号, 如果存在,返回顶点所在的序号,否则返回-1表示不存在
*/
public int getFirstNeighbour(int vertex) {
return neighbour(vertex, 0);
}
/**
* 返回序号为vertex的顶点相对于序号为currentAdjacentVertex的顶点的下一个邻接顶点的序号
*
* @param vertex 顶点序号
* @param currentAdjacentVertex currentAdjacentVertex为vertex序号顶点的邻接点,求相对于这个currentAdjacentVertex的下一个邻接顶点的序号
* @return 返回下一个邻接顶点的序号
*/
public int getNextNeighbour(int vertex, int currentAdjacentVertex) {
return neighbour(vertex, currentAdjacentVertex + 1);
}
/**
* 从firstSearchLocation查找获取顶点vertex序号的顶点的邻接点的序号,
*
* @param vertex 顶点序号
* @param firstSearchIndex 查找位置值的范围为[0, numberOfVertex - 1]
* @return 如果从firstSearchIndex开始查找存在返回邻接顶点,则返回邻接顶点的序号,否则返回1
*/
private int neighbour(int vertex, int firstSearchIndex) {
for (int i = firstSearchIndex; i < numberOfVertex; i++) {
if (edges[vertex][i] > 0) {
return i;
}
}
return -1;
}
public int getNumberOfEdges() {
return numberOfEdges;
}
public int getNumberOfVertex() {
return numberOfVertex;
}
}
class MinTree {
ArrayList<MSTEdge> mstEdges;
public MinTree(int numberOfVertex) {
mstEdges = new ArrayList<>(numberOfVertex - 1);
}
public void show() {
System.out.println("MinTree.show");
System.out.println("最小支撑树如下所示:");
mstEdges.stream()
.forEach(System.out::println);
}
public void addMstEdge(MSTEdge mstEdge) {
mstEdges.add(mstEdge);
}
public int numberOfMstEdge() {
return mstEdges.size();
}
/**
* @return 返回最小支撑树的最小权重
*/
public int getMinWeight() {
return mstEdges.stream()
.mapToInt(edge -> edge.getWeight())
.sum();
}
}
/**
* 最小支撑树的边类
*/
class MSTEdge {
int start;
int end;
int weight;
public MSTEdge(int start, int end, int weight) {
this.start = start;
this.end = end;
this.weight = weight;
}
@Override
public String toString() {
return "MSTEdge{" +
"start=" + start +
", end=" + end +
", weight=" + weight +
'}';
}
public int getEnd() {
return end;
}
public int getWeight() {
return weight;
}
}
/**
* 刘大有 普利姆算法实现
*/
class MinEdge {
/**
* vertex顶点,含义是已访问的顶点序号
*/
private int vertex;
/**
* 某个未访问顶点到vertex顶点所需要的最短的开销
*/
private int lowcost;
public int getVertex() {
return vertex;
}
public void setVertex(int vertex) {
this.vertex = vertex;
}
public int getLowcost() {
return lowcost;
}
public void setLowcost(int lowcost) {
this.lowcost = lowcost;
}
public MinEdge(int vertex, int lowcost) {
this.vertex = vertex;
this.lowcost = lowcost;
}
}
完整代码执行结果
Graph.show
[A, B, C, D, E, F, G]
[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0]
graph.getNumberOfEdges() = 0
graph.getNumberOfVertex() = 7
Graph.show
[A, B, C, D, E, F, G]
[0, 5, 7, 0, 0, 0, 2]
[5, 0, 0, 9, 0, 0, 3]
[7, 0, 0, 0, 8, 0, 0]
[0, 9, 0, 0, 0, 4, 0]
[0, 0, 8, 0, 0, 5, 4]
[0, 0, 0, 4, 5, 0, 6]
[2, 3, 0, 0, 4, 6, 0]
graph.getNumberOfEdges() = 10
graph.getNumberOfVertex() = 7
Graph.dfs
A->B->D->F->E->C->G->
C->A->B->D->F->E->G->
Graph.bfs
A->B->C->G->D->E->F->
C->A->E->B->G->F->D->
Graph.show
[A, B, C, D, E, F, G]
[2147483647, 5, 7, 2147483647, 2147483647, 2147483647, 2]
[5, 2147483647, 2147483647, 9, 2147483647, 2147483647, 3]
[7, 2147483647, 2147483647, 2147483647, 8, 2147483647, 2147483647]
[2147483647, 9, 2147483647, 2147483647, 2147483647, 4, 2147483647]
[2147483647, 2147483647, 8, 2147483647, 2147483647, 5, 4]
[2147483647, 2147483647, 2147483647, 4, 5, 2147483647, 6]
[2, 3, 2147483647, 2147483647, 4, 6, 2147483647]
graph.getNumberOfEdges() = 10
graph.getNumberOfVertex() = 7
MinTree.show
最小支撑树如下所示:
MSTEdge{start=6, end=0, weight=2}
MSTEdge{start=1, end=6, weight=3}
MSTEdge{start=4, end=6, weight=4}
MSTEdge{start=5, end=4, weight=5}
MSTEdge{start=3, end=5, weight=4}
MSTEdge{start=2, end=0, weight=7}
minTree.getMinWeight() = 25
MinTree.show
最小支撑树如下所示:
MSTEdge{start=6, end=0, weight=2}
MSTEdge{start=1, end=6, weight=3}
MSTEdge{start=4, end=6, weight=4}
MSTEdge{start=5, end=4, weight=5}
MSTEdge{start=3, end=5, weight=4}
MSTEdge{start=2, end=0, weight=7}
minTree2.getMinWeight() = 25
Disconnected from the target VM, address: '127.0.0.1:1925', transport: 'socket'
Process finished with exit code 0
下载
参考
总结
这个文章主要是讲述了MST构建最小支撑树的普利姆算法,深刻明确理解算法的每一个步骤,才能真正的写出这个算法,另外,就是思维天马行空,不受局限,因此必须真正上手敲一遍,在代码键入的过程中加入对算法的理解,才能融汇贯通。
有句话说的好,所有你想要的样子,都得靠自己来雕刻。
看了一个文章,上面讲述黄百鸣、李若彤很厉害,大体是在所纵欲的人生到底由多可怕,本意应该就是让人多自律,少放纵,节制自己的欲望吧,文章上说,只有不断对抗自己的欲望,做一些不那么好玩,不那么容易坚持的事情,比如健身、跑步、读书。
毁掉我们的不是我们所憎恨的东西,而恰恰是我们所热爱的东西
文章最后说的是如何让禁欲变成一种习惯?
- 延迟满足
- 禁欲,意味着放弃眼前的享乐,去未一个长远目标而努力。
- 循序渐进
- 只有循序渐进的努力才能让人适应变化。
- 正向激励
- 人们都不喜欢苦行僧的生活,适当奖励自己才能持续进步。
今年完成了韩顺平老师数据结构的学习,感觉很好,那么接下来就要认真的完成如下的文章
- 10大算法
- 图
- 树
- 8大排序算法

很多事情要做。
2020年6月26日12:04:33于AUX
























 1511
1511

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








