王道C语言笔记（中级算法篇）

目录

第一章：算法的基本概念

一、逻辑结构与空间结构

1、逻辑结构(对人友好）：数据元素之间的逻辑关系（抽象的）

2、存储结构（对计算机友好）：数据结构在计算机中的表示（具体的）

二、算法的基本概念

   1、程序=数据结构+算法

   2、算法（Algorithm）定义：是对特定问题求解步骤的描述，它是指令的有限序列，其中的每条指令表示一个或多个操作。

     3、算法的特性：

三、算法的时间复杂度（渐进时间复杂度）

1、如何计算：

2、常用技巧：

3、三种复杂度：

​三、算法的空间复杂度

1、如何计算：

2、常用技巧：​

​第二章：链表

一、线性表

1、定义：由n(n>=0)个相同类型的元素组成的有序集合。

2、线性表的特点：

3、注意：本小节描述的是线性表的逻辑结构，是独立于存储结构的；

二、顺序表(线性表的顺序表示)

1、逻辑上相邻的两个元素在物理位置上也相邻；

2、优点：

3、缺点：

 4、插入操作：

5、删除操作：

6、思考：动态分配的数组还属于顺序存储结构吗？

三、顺序表的初始化及插入操作实战

1、命名规范：变量名或者函数名

2、 业界命名规范:

四、顺序表的删除及查询

五、链表(线性表的链式表示)

1、顺序表：

2、单链表：

3、链表的优点：

4、链表的缺点：

5、链表的插入操作：

6、链表的删除操作：

7、链表的查找操作：

六、头插法新建链表

1、头插法新建链表流程：

七、尾插法新建链表

1、尾插法新建链表流程：​编辑

2、尾插法的特点是我们始终让尾指针r指向链表的尾部。

八、按位置查找及按值查找

1、按位置查找流程：​编辑

2、按值查找流程：

九、往第i个位置插入元素

1、往第i个位置插入元素流程：​编辑

十、链表的调试方法解析

十一、单链表的删除

1、单链表的删除操作流程：​编辑

第三章：栈

一、栈的原理解析

栈(stack):堆栈，又称为栈或堆叠，先进后出,后进先出1、栈：只允许在一端进行插入或删除操作的线性表栈顶*(Top);

2、S.top=-1时栈为空      S.top=MaxSize-1时栈满；

3、入栈：S.data[++S.top]=4 //前加加，先做加1，然后再去做其他运算      出栈：x=S.data[S.top--]

4、链式存储实现栈；

二、初始化栈-入栈-出栈实战

第四章：队列

一、循环队列

二、链表队列

第五章：二叉树

一、树与二叉树原理解析

1、树的定义：

2、树的特点：

3、二叉树的定义：

4、树结点数据结构:

二、二叉树层次建树

1、function.h文件：

2、main.cpp文件：

三、二叉树的深度优先搜索(DFS)

1、function.h文件：

2、main.cpp文件：

四、二叉树的广度优先搜索(BFS)

1、function.h文件：

2、main.cpp文件：

3、queue.cpp文件：

第六章：查找算法

一、顺序查找

二、二分查找（Binary Search）

1、二分查找又称折半查找，它仅适用于有序的顺序表（升序或降序）；

2、折半查找的基本思想:

3、针对顺序表有序，我们使用qsort来排序

4、折半查找代码：

三、二叉排序树（BST）

1、二叉排序树(也称二叉查找树)或者是一棵空树，或者是具有下列特性的叉树:

2、非递归与递归代码实战

3、二叉排序树删除 

第七章：排序算法

一、冒泡排序（Bubble Sort）

1、排序算法分为交换类排序，插入类排序，选择类排序，归并类排序

2、交换排序分为：

3、冒泡排序（冒泡排序考研中一般考选择题，考大题概率较低）：

 4、代码实战步骤:

5、时间复杂度与空间复杂度：

二、快速排序（Quick Sort）

1、快速排序的核心是分治思想（快速排序，简称快排，快排在考研初试中出大题的概率很高，也会出选择题，所以非常重要!）:

2、代码实战步骤:

3、假如每次快速排序数组都被平均地一分为二：

4、快速排序最差的时间复杂度为什么是n2呢?

5、快排的空间复杂度是 O(log2n)，因为递归的次数是log2n，而每次递归的形参都是需要占用空间的。

三、插入排序（Insertion Sort）

1、插入排序分为

2、如果一个序列只有一个数，那么该序列自然是有序的。

​编辑3、代码实战步骤：

4、时间复杂度与空间复杂度：

四、选择排序（Selection Sort）

1、选择排序分为

2、简单选择排序原理:

3、代码实战步骤：

4、时间复杂度与空间复杂度：

五、堆排序（Heap Sort）

1、堆(Heap)是计算机科学中的一种特殊的树状数据结构：

2、假设我们有3,87,2,93,78,56,61,38,12,40共10个元素我们将这10个元素建成一棵完全二叉树

3、代码实战步骤:

4、时间复杂度与空间复杂度：

六、归并排序（Merge sort）

1、如上图所示

 2、代码实战步骤：

3、时间复杂度与空间复杂度

---

第一章：算法的基本概念

一、逻辑结构与空间结构

1、逻辑结构(对人友好）：数据元素之间的逻辑关系（抽象的）

   分类：

        1、集合结构（无关系）
        2、线性结构（一对一），1在2的前面称为前驱，3在2的后面称为后继
        3、树形结构（一对多）
        4、图形结构（多对多）
    优点：
        1、可以实现随机存取；
        2、每个元素占用最少得空间。
    缺点：
        1、只能使用整块的存储单元，会产出较多的碎片。

2、存储结构（对计算机友好）：数据结构在计算机中的表示（具体的）

   分类：
        1、*顺序存储

        2、*链式存储：链式存储的基本单元是节点。
                    每个节点包含两个部分，一部分是数据域，用于存储实际的数据元素；另一部分是指针域，用于存储指向下一个节点的地址

        3、索引存储
        4、散列存储

    优点：
        1、充分利用所有的存储单元，不会出现碎片现象。
    缺点：
        1、需要额外的存储空间用来存放下一结点的指针；
        2、只能实现顺序存取。

二、算法的基本概念

   1、程序=数据结构+算法

        数据结构：如何用数据正确地描述现实世界的问题，并存入计算机；
        算法：如何高效地处理这些数据，以解决实际问题；

   2、算法（Algorithm）定义：是对特定问题求解步骤的描述，它是指令的有限序列，其中的每条指令表示一个或多个操作。

        例：要解决的问题：做番茄炒蛋
           食材：鸡蛋4个、西红柿2个、盐10g、糖30g
           步骤：1）、西红柿切块；
                2）、鸡蛋打匀；
                3）、将锅烧热，倒入鸡蛋翻炒；
                4）、倒入西红柿翻炒；
                5）、加入盐和糖；
                6）、装盘

     3、算法的特性：

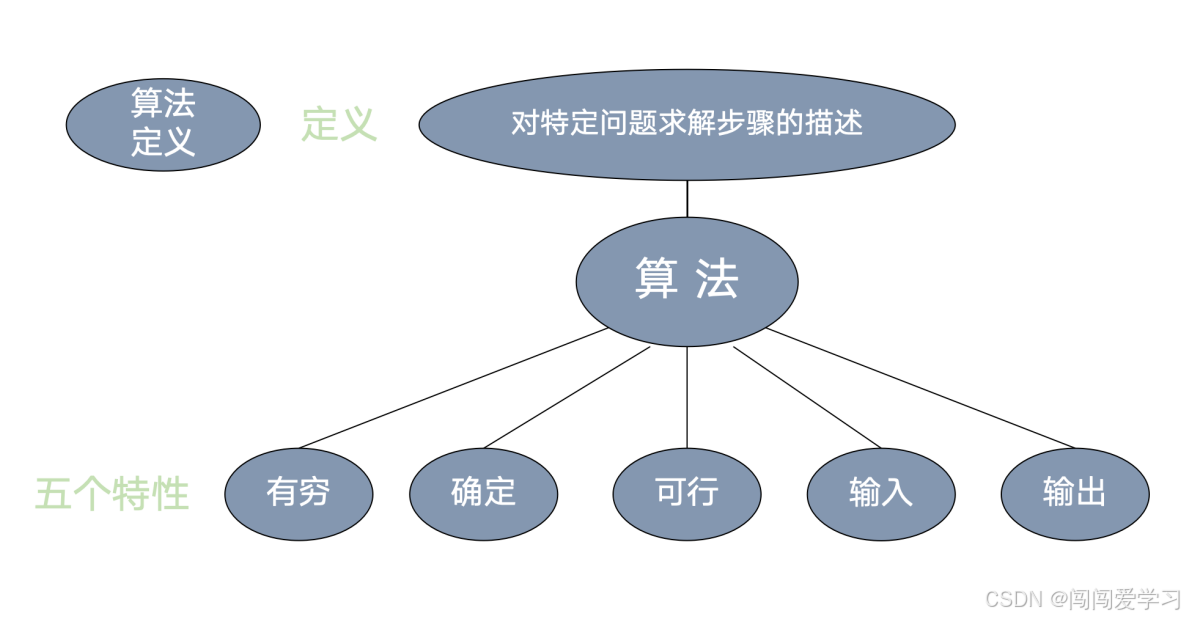
       1）、有穷：算法必须在执行有限步骤后结束，不能无限循环；
       2）、确定：算法的每一步都必须有确定的定义，不能有歧义；
       3）、可行：可以用已有的基本操作实现算法；
       4）、输入：算法可以有零个或多个输入，这些输入是算法执行所需的初始数据或条件；
       5）、输出：算法在结束时应该有一个或多个输出，这些输出是算法执行的结果；
       例：插入排序"8 1 5 9 3"=>"1 8 5 9 3"=>"1 5 8 9 3"=>"1 3 5 8 9";

三、算法的时间复杂度（渐进时间复杂度）

算法效率的度量：时间复杂度与空间复杂度；
算法时间复杂度：事前预估算法时间开销T(n)与问题规模n的关系（T表示"time");

1、如何计算：

1）、如何评估算法的时间开销：
让算法先运行，事后统计运行时间？
存在的问题：
    (1）、和机器性能有关；
    (2）、和编程语言有关，越高级的语言执行效率越低；
    (3）、和编译程序产生的机器指令质量有关；
    (4）、有些算法是不能事后再统计的；
2）、时间开销与问题规模n的关系，T(n)=3n+3=O(n),只考虑阶数，用大O记法表示
3）、当问题规模n足够大时，可以只考虑阶数高的部分；
4）、当问题规模n足够大时，常数项系数也可以忽略；
5）、大O表示“同阶”，同等数量级。即：当n->无穷时，两者之比为常数；
    （1）、T1(n)=O(n);
    （2）、T2(n)=O(n的二次方);
    （3）、T3(n)=O(n的三次方);
6)、顺序执行的代码只会影响常数项，可以忽略；
7)、只需挑循环中的一个基本操作分析它的执行次数与n的关系即可；
8）、如果有多层嵌套循环，只需关注最深层循环循环了几次；

2、常用技巧：

1）、加法规则：多项相加，只保留最高阶的项，且系数变为1
    例：T3(n)=n的三次方+n的二次方log2n=O（n的三次方）+O(n的二次方log2n）=O（n的二次方*n）+O(n的二次方log2n）=O(n的三次方)
2）、乘法规则：多项相乘，都保留；
3）、(常对幂指阶) O(1)<O(log2n)<O(n)<O(nlog2n)<O(n的二次方)<O(n的三次方)<O(2的n次方)<O(n!)<O(n的n次方);

3、三种复杂度：

1)、最坏时间复杂度：最坏情况下算法的时间复杂度；
2)、平均时间复杂度：所有输入实例等概率出现的情况下，算法的期望运行时间；
3)、最好时间复杂度：最好情况下算法的时间复杂度；

#include <stdio.h>

void loveYou(int n){//n为问题规模
    int i=1;//1
    while(i<=n){//3001,外层循环执行n次
        i=i*2;//每次翻倍
        printf("I Love You %d\n",i);//3000
//        for(int j=1;j<n;j++){//内层循环执行n的2次方
//            printf("I am Iron Man\n");
//        }
    }
    printf("I Love You More Than %d\n",n);//1
    //T(3000)=1+3001+2*3000+1,时间开销与问题规模n的关系，T(n)=3n+3
}

int main(){
    int m;
    scanf("%d",&m);
    loveYou(m);
    return 0;
}

三、算法的空间复杂度

空间复杂度：空间开销(内存开销)与问题规模n之间的关系

1、如何计算：

        普通程序：
           1、找到所占空间大小与问题规模相关的变量；
           2、分析所占空间x与问题规模n的关系x=f(n);
           3、x的数量级O(x)就是算法空间复杂度S(n);
       递归程序：
           1、找到递归调用的深度x与问题规模n的关系x=f(n);
           2、x的数量级O(x)就是算法空间复杂度S(n);
           3、注:有的算法各层函数所需存储空间不同，分析方法略有区别；

2、常用技巧：

        加法规则：O(f(n))+O(g(n))=O(max(f(n),g(n)),加法规则取阶数最大的那一项;
       乘法规则：O(f(n))*O(g(n))=O(f(n)*g(n));
       复杂度按照"常对幂指阶"大小进行排序;

#include <stdio.h>

//程序代码大小固定，与问题规模无关，S(n)=O(1),注:S表示"Space"
//数据，局部变量i，参数n... ...
//算法原地工作--算法所需内存空间为常量
void loveYou(int n){//n为问题规模
    int i=1;
    while(i<=n){
        i++;//每次+1
        printf("I Love You %d\n",i);
    }
    printf("I Love You More Than %d\n",n);
}

void test(int n){
    int flag[n];//假设一个int变量占4个字节，则所需内存空间为4+4n+4=4n+8，只需关注存储空间大小与问题规模相关的变量，S(n)=O(n)；
    int i;
}

void text(int n){
    int flag[n][n];//s(n)=O(n的2次方)+O(n)+O(1)=O(n的2次方),加法规则取阶数最大的那一项;
    int other[n];
    int i;
}

//函数递归调用带来的内存开销，S(n)=O(n);
void loveYou1(int n){//n为问题规模
    if(n>1){
        loveYou1(n-1);
    }
    printf("I Love You %d\n",n);
}

int main() {
    int n;
    scanf("%d",&n);
//    loveYou(n);
//    test(n);
//    text(n);
    loveYou1(n);
    return 0;
}

第二章：链表

一、线性表

1、定义：由n(n>=0)个相同类型的元素组成的有序集合。

        L=(a1,a2,... ...,ai-1,ai,ai+1,... ...,an)
       线性表中元素个数n，称为线性表的长度，当n=0时，为空表；
       a1是唯一的“第一个”数据元素，an是唯一的“最后一个”数据元素；
       ai-1为ai的直接前驱，ai+1为ai的直接后继；
       线性表中的元素是一一对应的。

2、线性表的特点：

       表中元素的个数是有限的；
       表中元素的数据类型都相同。意味着每一个元素占用相同大小的空间；
       表中元素具有逻辑上的顺序性，在序列中各元素排序有其先后顺序；

3、注意：本小节描述的是线性表的逻辑结构，是独立于存储结构的；

二、顺序表(线性表的顺序表示)

1、逻辑上相邻的两个元素在物理位置上也相邻；

2、优点：

       1）、可以随机存取（根据表头元素地址和元素序号）表中任意一个元素；
       2）、存储密度高，每个结点只存储数据元素；

3、缺点：

       1）、插入和删除操作需要移动大量元素；
       2）、线性表变化较大时，难以确定存储空间的容量；
       3）、存储分配需要一整段连续的存储空间，不够灵活；

 4、插入操作：

       1）、最好情况：在表位插入元素，不需要移动元素，时间复杂度为O(1);
       2）、最坏情况：在表头插入元素，所有元素依次后移，时间复杂度为O(n);
       3）、平均情况：在插入位置概率均等的情况下，平均移动元素的次数为n/2，时间复杂度为O(n);

5、删除操作：

       1）、最好情况：删除表尾元素，不需要移动元素，时间复杂度为O(1);
       2）、最坏情况：删除表头元素，之后的所有元素依次后移，时间复杂度为O(n);
       3）、平均情况：在删除位置概率均等的情况下，平均移动元素的次数为(n-1)/2，时间复杂度为O(n);

6、思考：动态分配的数组还属于顺序存储结构吗？

       1）、C的初试动态分配语句为：L.data=(ElemType)malloc(sizeof(ElemType)*IntiSize);
       2）、C++的初试动态分配语句为：L.data=new ElemType[InitSize];

#include <stdio.h>

#define MaxSize 50//定义线性表的长度
typedef struct{
    int data[MaxSize];//顺序表的元素
    int len;//顺序表的当前长度
}SqList;//顺序表的类型定义

int main() {
    //判断插入位置i是否合法（满足1<=i<=len+1)
    //判断存储空间是否已满（即插入x后是否会超出数组长度）
    /*int L[100];
    int i=1,x;
    for(int j=L.len;j>=i;j--){//将最后一个元素到第i个元素依次后移一位
        L.data[j]=L.data[j-1];
        L.data[i-1]=x;//空出的位置i处放入x
        L.len++;//线性表长度加1
    }
     */
    //注意：新型表的第一个元素的数组下标是0；
    return 0;
}

三、顺序表的初始化及插入操作实战

1、命名规范：变量名或者函数名

2、 业界命名规范:

        1）、下划线命名法，不同的单词用下划线例：list_insert；

        2）、驼峰命名法，每个单词首字母大写，例：ListInert；

#include <stdio.h>

#define MaxSize 50
typedef int ElemType;//让顺序表存储其他类型元素时，可以快速完成代码修改
//静态分配
typedef struct {
    ElemType data[MaxSize];
    int length;//当前顺序表中有多少个元素
}SqList;

//顺序表的插入，因为L会改变，因此我们这里要用引用,i是插入的位置
bool ListInsert(SqList &L,int i,ElemType element)
{
    //判断i是否合法,1<=i<=L.length+1
    if(i<1 || i>L.length+1){
        return false;
    }
    //如果存储空间满了，不能插入
    if(L.length==MaxSize){
        return false;//未插入成功返回false
    }
    //把后面的元素依次往后移动，空出位置，来放入要插入的元素
    for(int j=L.length;j>=i;j--)
    {
        L.data[j]=L.data[j-1];
    }
    L.data[i-1]=element;//放入要插入的元素
    L.length++;//顺序表长度要加1
    return true;//插入成功返回true
}

void PrintList(SqList L)
{
    int i;
    for(i=0;i<L.length;i++)
    {
        printf("%3d",L.data[i]);//为了打印到同一行
    }
    printf("\n");
}

//顺序表的初始化及插入操作实战
int main() {
    SqList L;//定义一个顺序表，变量L
    bool ret;//ret用来装函数的返回值
    L.data[0]=1;
    L.data[1]=2;
    L.data[2]=3;
    L.length=3;//设置长度
    ret= ListInsert(L,3,60);
    if(ret){
        printf("insert sqlist sucess\n");
        PrintList(L);
    }else{
        printf("insert sqlist failed\n");
    }
    return 0;
}

四、顺序表的删除及查询

#include <stdio.h>

#define MaxSize 50
typedef int ElemType;//让顺序表存储其他类型元素时，可以快速完成代码修改
//静态分配
typedef struct {
    ElemType data[MaxSize];
    int length;//当前顺序表中有多少个元素
}SqList;

//顺序表的插入，因为L会改变，因此我们这里要用引用,i是插入的位置
bool ListInsert(SqList &L,int i,ElemType element)
{
    //判断i是否合法,1<=i<=L.length+1
    if(i<1 || i>L.length+1){
        return false;
    }
    //如果存储空间满了，不能插入
    if(L.length==MaxSize){
        return false;//未插入成功返回false
    }
    //把后面的元素依次往后移动，空出位置，来放入要插入的元素
    for(int j=L.length;j>=i;j--)
    {
        L.data[j]=L.data[j-1];
    }
    L.data[i-1]=element;//放入要插入的元素
    L.length++;//顺序表长度要加1
    return true;//插入成功返回true
}

//打印顺序表
void PrintList(SqList L)
{
    int i;
    for(i=0;i<L.length;i++)
    {
        printf("%3d",L.data[i]);//为了打印到同一行
    }
    printf("\n");
}

//删除顺序表中的元素，i是要删除的元素的位置，del是为了获取被删除的元素的值
bool ListDelete(SqList &L,int i,ElemType &e)
{
    //判断删除的元素的位置是否合法
    if(i<1 || i>L.length)
    {
        return false;//一旦走到return函数就结束了
    }
    e=L.data[i-1];//首先保存要删除的元素的值
    int j;
    for(j=i;j<L.length;j++)//往前移动元素
    {
        L.data[j-1]=L.data[j];
    }
    L.length--;//顺序表长度减1
    return true;
}

int LocateElem(SqList L,ElemType element)
{
    int i;
    for(i=0;i<L.length;i++)
    {
        if(element==L.data[i])
        {
            return i+1;//因为i是数组的下表，加1后才是顺序表的下标
        }
    }
    return 0;//循环结束没找到
}

//顺序表的初始化及插入操作实战
int main() {
    SqList L;//定义一个顺序表，变量L
    bool ret;//ret用来装函数的返回值
    L.data[0]=1;
    L.data[1]=2;
    L.data[2]=3;
    L.length=3;//设置长度
    ret= ListInsert(L,2,60);
    if(ret){
        printf("insert sqlist success\n");
        PrintList(L);
    }else{
        printf("insert sqlist failed\n");
    }

    printf("------------------------\n");
    ElemType del;//删除的元素存入del中
    ret=ListDelete(L,1,del);
    if(ret)
    {
        printf("delete sqlist success\n");
        printf("del element=%d\n",del);
        PrintList(L);//顺序表打印
    }else{
        printf("delete sqlist failed\n");
    }

    int pos;//存储元素位置
    pos=LocateElem(L,60);
    if(pos)
    {
        printf("find this element\n");
        printf("element pos=%d\n",pos);
    }else{
        printf("don't find this element\n");
    }

    return 0;
}

五、链表(线性表的链式表示)

1、顺序表：

    1）、插入和删除操作移动大量元素；
    2）、数组的大小不好确定；
    3）、占用一大段连续的存储空间，造成很多碎片。

2、单链表：

    1）、逻辑上相邻的两个元素在物理位置上不相邻；
    2）、头指针：链表中第一个结点的存储位置，用来标识单链表;
    3）、头结点：在单链表第一个结点之前附加的一个结点，为了操作上的方便；

    4）、若链表有头结点，则头指针永远指向头结点，不论链表是否为空，头指针均不为空，头指针是链表的必须元素，他标识一个链表；
    5）、头结点是为了操作方便而设立的，其数据域一般为空，挥着存放链表的长度；
    6）、有头结点后，对在第一结点前插入和删除第一结点的操作就统一了，不需要频繁重置头指针，但头结点不是必须得。

3、链表的优点：

    1）、插入和删除操作不需要移动元素；
    2）、不需要大量的连续存储空间；

4、链表的缺点：

   1）、单链表附加指针域，也存在浪费存储空间的缺点；
   2）、 查找操作时需要从表头开始遍历，依次查找，不能随机存取；

5、链表的插入操作：

    1）、表头&表中插入元素:
        q->next=p->next;
        p->next=q;
    2)、表尾插入元素:
        p->next=q;
        q->next=NULL;

6、链表的删除操作：

    p=GetElem(L,i-1);//查找删除位置的前驱节点
    q=p->next;//p->next 就是要删除的元素所在的节点,将其存储在 q 指针中
    p->next=q->next;//将p的next指针指向q的next指针所指向的节点。
                    //这样，原本p指向q，现在p直接指向了q后面的节点，使得q节点从链表中断开，实现了逻辑上的“断链”操作。
    free(q);//最后使用 free(q) 释放 q 所指向节点的内存

7、链表的查找操作：

     1）、按序号查找结点值的算法如下：

LNode *p=L->next;
        int j=1;
        while(p&&j<i){
            p=p->next;
            j++;
        }
        return p;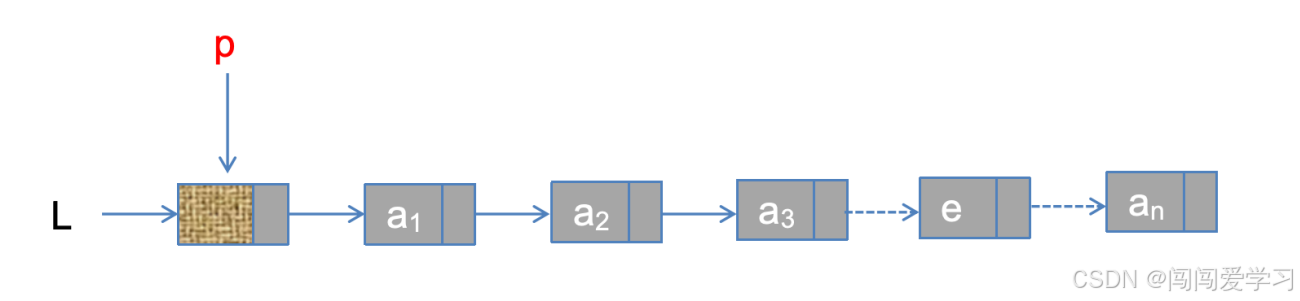

      2）、按值查找结点的算法如下：
       

 LNode *p=L->next;
        while(p!=NULL&&p->data!=e){
            p=p->next;
        }
        return p;

六、头插法新建链表

1、头插法新建链表流程：

#include <stdio.h>
#include <stdlib.h>

typedef int ElemType;
typedef struct LNode
{
    ElemType data;//数据域
    struct LNode *next;//指针域
}LNode,*LinkList;

//LNode*是结构体指针和LinkList是完全等价的
void list_head_insert(LinkList &L)//LNode* &L
{
    L=(LinkList)malloc(sizeof(LNode));//为头指针申请空间，得到了头结点的空间
    L->next=NULL;
    ElemType X;
    scanf("%d",&X);
    LNode *s;//s是用来只想申请的新结点
    while(X!=9999)
    {
        s=(LinkList)malloc(sizeof(LNode));
        s->data=X;
        s->next=L->next;//s的next指向原本链表的第一个结点
        L->next=s;//头结点的next指向的新结点
        scanf("%d",&X);
    }

}

void PrintList(LinkList L)
{
    L=L->next;
    while(L!=NULL)
    {
        printf("%3d",L->data);
        L=L->next;
    }
    printf("\n");
}

//头插法来新建链表
int main()
{
    LinkList L;//L是链表头指针，是结构体指针类型
    list_head_insert(L);//输入数据可以为3 4 5 6 7 9999，头插法新建链表
    PrintList(L);
    return 0;
}

七、尾插法新建链表

1、尾插法新建链表流程：

2、尾插法的特点是我们始终让尾指针r指向链表的尾部。

#include <stdio.h>
#include <stdlib.h>

typedef int ElemType;
typedef struct LNode
{
    ElemType data;//数据域
    struct LNode *next;//指针域
}LNode,*LinkList;

//LNode*是结构体指针和LinkList是完全等价的
void list_head_insert(LinkList &L)//LNode* &L
{
    L=(LinkList)malloc(sizeof(LNode));//为头指针申请空间，得到了头结点的空间
    L->next=NULL;
    ElemType X;
    scanf("%d",&X);
    LNode *s;//s是用来只想申请的新结点
    while(X!=9999)
    {
        s=(LinkList)malloc(sizeof(LNode));
        s->data=X;
        //头插法插入
        s->next=L->next;//s的next指向原本链表的第一个结点
        L->next=s;//头结点的next指向的新结点

        scanf("%d",&X);
    }

}

void list_tail_insert(LNode* &L)
{
    L=(LinkList)malloc(sizeof(LNode));//为头指针申请空间，得到了头结点的空间
    L->next=NULL;
    ElemType X;
    scanf("%d",&X);
    LNode *s,*r=L;//s是用来只想申请的新结点,r是始终指向链表尾部
    while(X!=9999)
    {
        s=(LinkList)malloc(sizeof(LNode));//为新结点申请新空间
        s->data=X;
        //尾插法插入
        r->next=s;//新结点给尾结点的next指针
        r=s;//r要指向新的尾部

        scanf("%d",&X);
    }
    r->next=NULL;//让尾结点的next为NULL
}

void PrintList(LinkList L)
{
    L=L->next;
    while(L!=NULL)
    {
        printf("%3d",L->data);
        L=L->next;
    }
    printf("\n");
}

//尾插法来新建链表
int main()
{
    LinkList L;//L是链表头指针，是结构体指针类型
    //list_head_insert(L);//输入数据可以为3 4 5 6 7 9999，头插法新建链表
    list_tail_insert(L);//尾插法新建链表
    PrintList(L);
    return 0;
}

八、按位置查找及按值查找

1、按位置查找流程：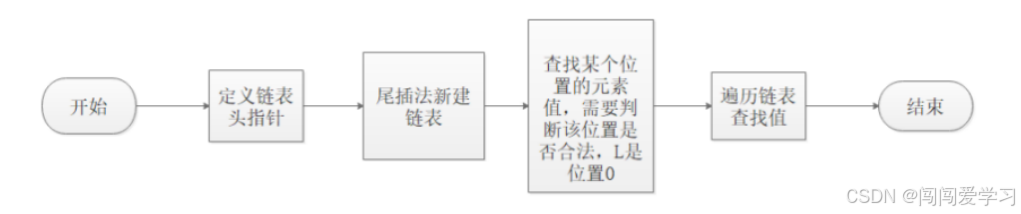

2、按值查找流程：

        开始=>定义链表头指针=>尾插法新建链表=>查找对应的元素值，如果找到对应的值，就返回那个结点的地址=>遍历链表查找值=>结束

#include <stdio.h>
#include <stdlib.h>

typedef int ElemType;
typedef struct LNode
{
    ElemType data;//数据域
    struct LNode *next;//指针域
}LNode,*LinkList;

//LNode*是结构体指针和LinkList是完全等价的
void list_head_insert(LinkList &L)//LNode* &L
{
    L=(LinkList)malloc(sizeof(LNode));//为头指针申请空间，得到了头结点的空间
    L->next=NULL;
    ElemType X;
    scanf("%d",&X);
    LNode *s;//s是用来只想申请的新结点
    while(X!=9999)
    {
        s=(LinkList)malloc(sizeof(LNode));
        s->data=X;
        //头插法插入
        s->next=L->next;//s的next指向原本链表的第一个结点
        L->next=s;//头结点的next指向的新结点

        scanf("%d",&X);
    }

}

void list_tail_insert(LNode* &L)
{
    L=(LinkList)malloc(sizeof(LNode));//为头指针申请空间，得到了头结点的空间
    L->next=NULL;
    ElemType X;
    scanf("%d",&X);
    LNode *s,*r=L;//s是用来只想申请的新结点,r是始终指向链表尾部
    while(X!=9999)
    {
        s=(LinkList)malloc(sizeof(LNode));//为新结点申请新空间
        s->data=X;
        //尾插法插入
        r->next=s;//新结点给尾结点的next指针
        r=s;//r要指向新的尾部

        scanf("%d",&X);
    }
    r->next=NULL;//让尾结点的next为NULL
}

void PrintList(LinkList L)
{
    L=L->next;
    while(L!=NULL)
    {
        printf("%3d",L->data);
        L=L->next;
    }
    printf("\n");
}

//按位置查找
LinkList GetElem(LinkList L,int SearchPos)
{
    int i=0;
    if(SearchPos<0)
    {
        return NULL;
    }
    while(L&&i<SearchPos)//L!=NULL
    {
        L=L->next;
        i++;
    }
    return L;
}

LinkList LocateElem(LinkList L,ElemType SearchVal)
{
    while(L)
    {
        if(L->data==SearchVal)//如果找到对应的值，就返回那个结点的地址
        {
            return L;
        }
        L=L->next;
    }
    return NULL;
}

//尾插法来新建链表
int main()
{
    LinkList L,search;//L是链表头指针，是结构体指针类型，search用来存储拿到的某一个节点
    //list_head_insert(L);//输入数据可以为3 4 5 6 7 9999，头插法新建链表
    list_tail_insert(L);//尾插法新建链表
    PrintList(L);//链表打印

    //按位置查找
    search=GetElem(L,2);
    if(search!=NULL)
    {
        printf("Succeed in searching by serial number\n");
        printf("%d\n",search->data);
    }

    //按值查找
    search=LocateElem(L,6);
    if(search!=NULL)
    {
        printf("Succeed by value succeeded\n");
        printf("%d\n",search->data);
    }
    return 0;
}

九、往第i个位置插入元素

1、往第i个位置插入元素流程：

#include <stdio.h>
#include <stdlib.h>

typedef int ElemType;
typedef struct LNode
{
    ElemType data;//数据域
    struct LNode *next;//指针域
}LNode,*LinkList;

//LNode*是结构体指针和LinkList是完全等价的
void list_head_insert(LinkList &L)//LNode* &L
{
    L=(LinkList)malloc(sizeof(LNode));//为头指针申请空间，得到了头结点的空间
    L->next=NULL;
    ElemType X;
    scanf("%d",&X);
    LNode *s;//s是用来只想申请的新结点
    while(X!=9999)
    {
        s=(LinkList)malloc(sizeof(LNode));
        s->data=X;
        //头插法插入
        s->next=L->next;//s的next指向原本链表的第一个结点
        L->next=s;//头结点的next指向的新结点

        scanf("%d",&X);
    }

}

void list_tail_insert(LNode* &L)
{
    L=(LinkList)malloc(sizeof(LNode));//为头指针申请空间，得到了头结点的空间
    L->next=NULL;
    ElemType X;
    scanf("%d",&X);
    LNode *s,*r=L;//s是用来只想申请的新结点,r是始终指向链表尾部
    while(X!=9999)
    {
        s=(LinkList)malloc(sizeof(LNode));//为新结点申请新空间
        s->data=X;
        //尾插法插入
        r->next=s;//新结点给尾结点的next指针
        r=s;//r要指向新的尾部

        scanf("%d",&X);
    }
    r->next=NULL;//让尾结点的next为NULL
}

void PrintList(LinkList L)
{
    L=L->next;
    while(L!=NULL)
    {
        printf("%3d",L->data);
        L=L->next;
    }
    printf("\n");
}

//按位置查找
LinkList GetElem(LinkList L,int SearchPos)
{
    int i=0;
    if(SearchPos<0)
    {
        return NULL;
    }
    while(L&&i<SearchPos)//L!=NULL
    {
        L=L->next;
        i++;
    }
    return L;
}

//按值查找
LinkList LocateElem(LinkList L,ElemType SearchVal)
{
    while(L)
    {
        if(L->data==SearchVal)//如果找到对应的值，就返回那个结点的地址
        {
            return L;
        }
        L=L->next;
    }
    return NULL;
}

//往第i个位置插入元素
bool ListFrontInsert(LinkList L,int i,ElemType InsertVal)
{
    LinkList p= GetElem(L,i-1);
    if(NULL==p)
    {
        return false;
    }
    LinkList q;
    q=(LinkList)malloc(sizeof(LNode));//为新结点申请空间
    q->data=InsertVal;//往申请的新结点放入要插入的值

    q->next=p->next;//新结点指向下一个结点
    p->next=q;//上一个结点指向新结点
    return true;
}

//尾插法来新建链表
int main()
{
    LinkList L,search;//L是链表头指针，是结构体指针类型，search用来存储拿到的某一个节点
    //list_head_insert(L);//输入数据可以为3 4 5 6 7 9999，头插法新建链表
    list_tail_insert(L);//尾插法新建链表
    PrintList(L);//链表打印

    bool ret;
    ret=ListFrontInsert(L,6,99);//新结点插入第i个位置
    PrintList(L);

    return 0;
}

十、链表的调试方法解析

        链表因为每一个结点在内存中式不连续的，因此是不适合看内存视图的，可以通过单步调试，直接在变量窗口，把头指针L，依次点开，观察每一个结点是否符合自己的预期。

#include <stdio.h>
#include <stdlib.h>

typedef int ElemType;
typedef struct LNode
{
    ElemType data;//数据域
    struct LNode *next;//指针域
}LNode,*LinkList;

//LNode*是结构体指针和LinkList是完全等价的
void list_head_insert(LinkList &L)//LNode* &L
{
    L=(LinkList)malloc(sizeof(LNode));//为头指针申请空间，得到了头结点的空间
    L->next=NULL;
    ElemType X;
    scanf("%d",&X);
    LNode *s;//s是用来只想申请的新结点
    while(X!=9999)
    {
        s=(LinkList)malloc(sizeof(LNode));
        s->data=X;
        //头插法插入
        s->next=L->next;//s的next指向原本链表的第一个结点
        L->next=s;//头结点的next指向的新结点

        scanf("%d",&X);
    }

}

void list_tail_insert(LNode* &L)
{
    L=(LinkList)malloc(sizeof(LNode));//为头指针申请空间，得到了头结点的空间
    L->next=NULL;
    ElemType X;
    scanf("%d",&X);
    LNode *s,*r=L;//s是用来只想申请的新结点,r是始终指向链表尾部
    while(X!=9999)
    {
        s=(LinkList)malloc(sizeof(LNode));//为新结点申请新空间
        s->data=X;
        //尾插法插入
        r->next=s;//新结点给尾结点的next指针
        r=s;//r要指向新的尾部

        scanf("%d",&X);
    }
    r->next=NULL;//让尾结点的next为NULL
}

void PrintList(LinkList L)
{
    L=L->next;
    while(L!=NULL)
    {
        printf("%3d",L->data);
        L=L->next;
    }
    printf("\n");
}

//按位置查找
LinkList GetElem(LinkList L,int SearchPos)
{
    int i=0;
    if(SearchPos<0)
    {
        return NULL;
    }
    while(L&&i<SearchPos)//L!=NULL
    {
        L=L->next;
        i++;
    }
    return L;
}

//按值查找
LinkList LocateElem(LinkList L,ElemType SearchVal)
{
    while(L)
    {
        if(L->data==SearchVal)//如果找到对应的值，就返回那个结点的地址
        {
            return L;
        }
        L=L->next;
    }
    return NULL;
}

//往第i个位置插入元素
bool ListFrontInsert(LinkList L,int i,ElemType InsertVal)
{
    LinkList p= GetElem(L,i-1);
    if(NULL==p)
    {
        return false;
    }
    LinkList q;
    q=(LinkList)malloc(sizeof(LNode));//为新结点申请空间
    q->data=InsertVal;//往申请的新结点放入要插入的值

    q->next=p->next;//新结点指向下一个结点
    p->next=q;//上一个结点指向新结点
    return true;
}

//尾插法来新建链表
int main()
{
    LinkList L,search;//L是链表头指针，是结构体指针类型，search用来存储拿到的某一个节点
    //list_head_insert(L);//输入数据可以为3 4 5 6 7 9999，头插法新建链表
    list_tail_insert(L);//尾插法新建链表
    PrintList(L);//链表打印

    bool ret;
    ret=ListFrontInsert(L,6,99);//新结点插入第i个位置
    PrintList(L);

    return 0;
}

十一、单链表的删除

1、单链表的删除操作流程：

#include <stdio.h>
#include <stdlib.h>

typedef int ElemType;
//定义了一个结构体 LNode
typedef struct LNode{
    ElemType data;//数据域
    struct LNode *next;//指针域
}LNode,*LinkList;

//尾插法新建链表
void list_tail_insert(LinkList &L)
{
    L=(LinkList)malloc(sizeof(LNode));
    L->next=NULL;
    ElemType x;
    LinkList s,r=L;//表达有个结点指向尾部
    scanf("%d",&x);
    while(x!=9999)
    {
        s=(LinkList) malloc(sizeof(LNode));//给新结点申请空间
        s->data=x;//把读取到的数据放入新结点的数据域
        r->next=s;//原有链表的指针域next,指向新结点的数据域
        r=s;//尾指针要指向新的尾结点
        scanf("%d",&x);
    }
    r->next=NULL;//尾结点的next要为NULL
}

//按位置查找
LinkList GetElem(LinkList L,int SearchPos)
{
    int i=0;
    if(SearchPos<0)
    {
        return NULL;
    }
    while(L&&i<SearchPos)//L!=NULL
    {
        L=L->next;
        i++;
    }
    return L;
}

//链表遍历，并打印数据
void PrintList(LinkList L)
{
    L=L->next;//去到第一个结点
    while(L!=NULL)
    {
        printf("%d",L->data);//打印当前结点数据
        L=L->next;//指向下一个结点
        if(L!=NULL)
        {
            printf(" ");
        }
    }
    printf("\n");
}

//删除第i个位置的元素
//删除时L是不会变的，所以不需要加引用
bool ListDelete(LinkList L,int i)
{
    LinkList p = GetElem(L,i-1);//拿到要删除结点的前一个结点
    if(NULL==p)
    {
        return false;
    }
    LinkList q = p->next;//拿到要删除的结点指针
    if(NULL==q)//当链表只有n个结点，删除第n+1个结点，出现这种异常情况时，避免程序崩溃
    {
        return false;
    }
    p->next=q->next;//断链
    free(q);//释放删除结点的内存
    return true;
}

int main()
{
    LinkList L;//链表头指针，代表链表
    list_tail_insert(L);//尾插法新建链表
    PrintList(L);

    ListDelete(L,4);//删除第4个位置的元素
    PrintList(L);//链表遍历并打印
    return 0;
}

第三章：栈

一、栈的原理解析

栈(stack):堆栈，又称为栈或堆叠，先进后出,后进先出
1、栈：只允许在一端进行插入或删除操作的线性表栈顶*(Top);

2、S.top=-1时栈为空
      S.top=MaxSize-1时栈满；

3、入栈：S.data[++S.top]=4 //前加加，先做加1，然后再去做其他运算
      出栈：x=S.data[S.top--]

元素出栈：

栈空栈满：

4、链式存储实现栈；

#include <stdio.h>

typedef int Elemtype;
typedef struct{
    Elemtype data[50];
    int top;
}SqStack;

int main() {
    SqStack S;

    return 0;
}

二、初始化栈-入栈-出栈实战

1、代码实战步骤依次为初始化栈，判断栈是否为空，压栈，获取栈顶元素，弹栈。
2、注意S.top为-1时，代表栈为空，我们每次是先对S.top加1后，在放置元素。

#include <stdio.h>

#define MaxSize 50
typedef int ElemType;
typedef struct{
    ElemType data[MaxSize];//数组
    int top;//始终指向栈顶的一个变量
}SqStack;

//初始化栈
void InitStack(SqStack &S)
{
    S.top=-1;//初始化栈，就是S.top=-1，让栈为空
}

//判断栈顶是否为已经初始化过的
bool StackEmpty(SqStack S)
{
    if(-1==S.top)
    {
        return true;
    }else{
        return false;
    }
}

//入栈
bool Push(SqStack &S,ElemType x)
{
    //判断栈是否满了
    if(S.top==MaxSize-1)
    {
        return false;
    }
    S.data[++S.top]=x;//等价于S.top=S.top+1; S.data[S.top]=x;
    return true;
}

//获取栈顶元素
bool GetTop(SqStack S,ElemType &m)
{
    if(StackEmpty(S))
    {
        return false;
    }
    m=S.data[S.top];//拿栈顶元素
    return true;
}

//弹栈,弹栈是改变栈顶指针top
bool Pop(SqStack &S,ElemType &m)
{
    if(StackEmpty(S))
    {
        return false;
    }
    m=S.data[S.top--];//出栈 后减减等价于 先m=S.data[S.top]; S.top=S.top-1;
    return true;
}

int main() {
    SqStack S;
    InitStack(S);
    bool flag;
    flag=StackEmpty(S);
    if(flag)
    {
        printf("stack is empty\n");
    }
    Push(S,3);//入栈元素为3
    Push(S,4);//入栈元素为4
    Push(S,5);//入栈元素为5

    ElemType m;
    flag=GetTop(S,m);//获取栈顶元素
    if(flag)
    {
        printf("get top %d\n",m);
    }

    flag=Pop(S,m);
    if(flag)
    {
        printf("pop element %d\n",m);
    }
    return 0;
}

第四章：队列

一、循环队列

1、队列（Queue）简称为队，特性是先进先出（First in First Out,FIFO)，也是一种操作受限的线性表，只允许在表的一端进行插入，而在标的另一端进行删除。
2、向队列中插入元素称为入队或进队，删除元素称为出队或离队。

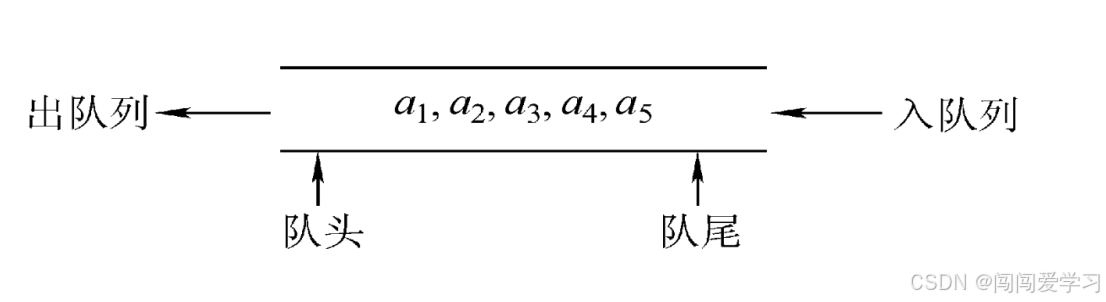
3、队头（Front），允许删除的一端，又称为队首；
      队尾（Rear),允许插入的一端。

4   、循环队列

#define MaxSize 5
    typedef int ElemType;
    typedef struct{
        ElemType data[MaxSize];//数组，存储MaxSize-1个元素
        int front,rear;//队列头 队列尾
    }SqStack;

    SqQueue Q;

5、（Q.rear+1）%MaxSize==Q.front  判断队列满的方法
6、循环队列元素入队

bool EnQueue(SqQueue &Q,ElemType x)
    {
        if((Q.rear+1）%MaxSize==Q.front)//判断是否队满
            return false;
        Q.data[Q.rear]=x//放入元素
        Q.rear=(Q.rear+1）%MaxSize;//改变队尾标记
        return true;

7、循环队列元素出队

 bool DeQueue(SqQueue &Q,ElemType x)
    {
        if(Q.rear==Q.front)//先判断队列是否为空
            return false;
        x=Q.data[Q.front]//先进先出
        Q.front=(Q.rear+1）%MaxSize;
        return true;

8、队列的链式存储

    队列的链式表示称为链队列，他实际上是一个同事带有队头指针和队尾指针的单链表。
    头指针指向队头结点，队尾指针指向队尾结点，即单链表的最后一个结点。
   动画网站：Linked List Queue Visualization https://www.cs.usfca.edu/~galles/visualization/QueueLL.htmlhttps://www.cs.usfca.edu/~galles/visualization/QueueLL.htmlhttps://www.cs.usfca.edu/~galles/visualization/QueueLL.htmlhttps://www.cs.usfca.edu/~galles/visualization/QueueLL.htmlhttps://www.cs.usfca.edu/~galles/visualization/QueueLL.htmlhttps://www.cs.usfca.edu/~galles/visualization/QueueLL.html
    存储结构：
       

 typedef int ElemType；
        typedef struct LinkNode{
            ElemType data;
            struct LinkNode *next;
        }LinkNode;//链表结点的结构体
        typedef struct{
            LinkNode *front,*rear;//链表头 链表尾
        }LinkQueue;//先进先出
        LinkQueue Q;

#include <stdio.h>


#define MaxSize 50
typedef int ElemType;
typedef struct{
    ElemType data[MaxSize];
    int front,rear;
}SqQueue;

void InitQueue(SqQueue &Q)
{
    Q.front=Q.rear=0;//初始化循环队列，就是让头和尾都指向零号
}

//判断循环队列是否为空
bool IsEmpty(SqQueue Q)
{
    return Q.rear==Q.front;
}
//入队
bool EnQueue(SqQueue &Q,ElemType x)
{
    if((Q.rear+1)%MaxSize==Q.front)//判断循环队列是否满了，满了就不能入队了
    {
        return false;
    }
    Q.data[Q.rear]=x;//放入元素
    Q.rear=(Q.rear+1)%MaxSize;//rear要加1，如果大于数组最大下标，就要回到开头
    return true;
}

//出队
bool DeQueue(SqQueue &Q,ElemType &x)
{
    if(Q.rear==Q.front)//判断队列是否为空，如果队列为空无法出队
    {
        return false;
    }
    x=Q.data[Q.front];//出队
    Q.front=(Q.front+1)%MaxSize;
}

//循环队列的代码实战
int main() {
    SqQueue Q;
    InitQueue(Q);
    bool ret;
    ret=IsEmpty(Q);
    if(ret)
    {
        printf("SqQueue is Empty\n");
    }
    EnQueue(Q,3);
    EnQueue(Q,4);
    EnQueue(Q,5);
    ret=EnQueue(Q,6);
    ret=EnQueue(Q,7);
    if(ret)
    {
        printf("EnQueue success\n");
    }else{
        printf("EnQueue false\n");
    }

    ElemType element;//存储出队元素
    DeQueue(Q,element);//
    if(ret)
    {
        printf("DeQueue success\n");
    }else{
        printf("DeQueue false\n");
    }
    return 0;
}

9、步骤依次为：初始化循环队列、判断循环队列是否为空，入队，出队；
10、注意代码执行结束可以通过调试来观察循环队列内的元素，同时注意新建项目是C++可执行程序；

二、链表队列

1、步骤：初始化队列、入队、出队；
2、注意代码执行结束可以通过调试来观察队列内的元素，同时注意新建项目是C++可执行程序；

#include <stdio.h>
#include <stdlib.h>

typedef int ElemType;
typedef struct LinkNode{
    ElemType data;
    struct LinkNode *next;
}LinkNode;

typedef struct{
    LinkNode *front,*rear;//链表头 链表尾
}LinkQueue;//先进先出

void InitQueue(LinkQueue &Q)
{
    Q.front=Q.rear=(LinkNode*)malloc(sizeof(LinkNode));//头和尾指向同一个结点
    Q.front->next=NULL;

}

//入队
void EnQueue(LinkQueue &Q,ElemType x)
{
    LinkNode *pnew=(LinkNode*)malloc(sizeof(LinkNode));
    pnew->data=x;
    pnew->next=NULL;//要让next为NULL
    Q.rear->next=pnew;//尾指针的next指向pnew，因为从尾部入队
    Q.rear=pnew;//rear要指向新的尾部
}

//出队
bool DeQueue(LinkQueue &Q,ElemType &x)
{
    if(Q.rear==Q.front)//队列为空
    {
        return false;
    }
    LinkNode* q=Q.front->next;//拿到第一个结点,存入q
    x=q->data;//获取要出队的元素值
    Q.front->next=q->next;//让第一个结点断链
    if(Q.rear==q)
    {
        Q.rear=Q.front;//链表只剩余一个结点时，被删除后，要改变rear
    }
    free(q);
    return true;
}

//通过链表来实现队列
int main() {
    LinkQueue Q;
    InitQueue(Q);//初始化队列

    EnQueue(Q,3);
    EnQueue(Q,4);
//    EnQueue(Q,5);
//    EnQueue(Q,6);
//    EnQueue(Q,7);
    bool ret;
    ElemType element;
    ret=DeQueue(Q,element);
    if(ret)
    {
        printf("DeQueue success element=%d\n",element);
    }else{
        printf("DeQueue failed\n");
    }
    DeQueue(Q,element);
    ret=DeQueue(Q,element);
    if(ret)
    {
        printf("DeQueue success element=%d\n",element);
    }else{
        printf("DeQueue failed\n");
    }
    return 0;
}

第五章：二叉树

一、树与二叉树原理解析

1、树的定义：

        是n(n>0)个节点的有限集，当n=0时称为空树。在任意一棵非空树中应满足:1)有且仅有一个特定的称为根的结点，
         当n>1时，其余节点可分为m(m>0)个2)互不相交的有限集T1,T2……，Tm，其中每个集合本身又是一棵树，并且称为根的子树。

2、树的特点：

        树作为一种逻辑结构，同时也是一种分层结构，具有以下两个特点:
                1)、树的根结点没有前驱，除根结点外的所有结点有且只有一个前驱；
                2)、树中所有结点可以有零个或多个后继；

3、二叉树的定义：

        二叉树是另一种树形结构，其特点是每个结点至多只有两棵子树(即二叉树中不存在度大于2的结点)，并且二叉树的子树有左右之分，其次序不能任意颠倒.
        与树相似，二叉树也以递归的形式定义。二叉树是n(n20)个结点的有限集合:
                1)、或者为空二叉树，即n=0；
                2)、或者由一个根结点和两个互不相交的被称为根的左子树和右2子树组成。左子树和右子树又分别是一棵二叉树。

1）、 满二叉树 (Full Binary Tree)

• 定义：
  一棵深度为 ℎh 的二叉树，每一层的节点都达到最大数量。即：

  • 所有叶子节点位于最后一层。

  • 非叶子节点均有 2个子节点。

  • 总节点数为 2ℎ−12h−1（ℎ≥1h≥1）。

• 特点：

  • 严格填满每一层，无空缺。

  • 常见于需要严格平衡的场景（如哈夫曼编码树）。

2、完全二叉树 (Complete Binary Tree)

• 定义：
  一棵深度为 ℎh 的二叉树，满足：

  • 前 ℎ−1h−1 层节点全满。

  • 最后一层节点从左到右连续排列，无中间空缺。

  • 总节点数范围为 [2ℎ−1,2ℎ−1][2h−1,2h−1]。

• 特点：

  • 允许最后一层不满，但必须左对齐。

  • 适合用数组存储（父子节点下标关系明确）。

  • 是堆结构（如优先队列）的基础。

3）、区别

4、树结点数据结构:

树中任何一个结点都是一个结构体，它的空间我们是通过maloc申请出来

typedef char BiElemType;
typedef struct BiTNode{
   BiElemType c;//c就是书籍上的data
   struct BiTNode *lchild;
   struct BiTNode *rchild;
}BiTNode,*BiTree,

二、二叉树层次建树

为了提高代码的编写效率,我们把结构体类型的声明放入function.h头文件,function.h头文件在 main.cpp 进行了include，最终树建的对不对，我们可以通过单步调试来看树的结果，断点打在return0位置。

1、function.h文件：

#include <stdio.h>
#include <stdlib.h>

typedef char BiElemType;
typedef struct BiTNode{
    BiElemType c;//就是书籍上的data
    struct BiTNode *lchild;
    struct BiTNode *rchild;
}BiTNode,*BiTree;

//tag结构体四辅助队列使用的
typedef struct tag{
    BiTree p;//树的某一个结点的地址值
    struct tag *pnext;
}tag_t,*ptag_t;

2、main.cpp文件：

#include "function.h"

int main()
{
    BiTree pnew;//用来指向新申请的树结点
    char c;
    BiTree tree=NULL;//tree是指向树根的，代表树
    ptag_t phead=NULL,ptail=NULL,listpnew=NULL,pcur;//phead就是队列头，ptail就是队列尾
    //输入内容为abcdefghij
    while(scanf("%c",&c)) {
        if (c == '\n') {
            break;//读取到换行就结束
        }
        //calloc申请的空间大小是两个参数直接相乘，calloc申请空间并对空间进行初始化，并赋值为0
        pnew = (BiTree) calloc(1, sizeof(BiTNode));
        pnew->c = c;//将数据放进去
        listpnew = (ptag_t) calloc(1, sizeof(tag_t));//给队列结点申请空间
        listpnew->p = pnew;
        //如果是树的第一个结点
        if (NULL == tree) {
            tree = pnew;//tree指向树的根结点
            phead = listpnew;//第一个结点既是队列头也是队列尾
            ptail = listpnew;
            pcur = listpnew;//pcur要指向进入树的父亲元素
        } else {
            //让元素先入队列
            ptail->pnext = listpnew;//新结点放入链表，通过尾插法
            ptail = listpnew;//ptail指向队列尾部
            //接下来把b结点放入树种
            if (NULL==pcur->p->lchild) {
                pcur->p->lchild = pnew;//pcur->左孩子为空，就放入左孩子
            } else if (NULL == pcur->p->rchild) {
                pcur->p->rchild = pnew;//pcur->p右孩子为空，就放入右孩子
                pcur = pcur->pnext;//当前结点左右孩子都有了，pcur就指向下一个
            }
        }
    }
    return 0;
}

三、二叉树的深度优先搜索(DFS)

1、function.h文件：

#include <stdio.h>
#include <stdlib.h>

typedef char BiElemType;
typedef struct BiTNode{
    BiElemType c;//就是书籍上的data
    struct BiTNode *lchild;
    struct BiTNode *rchild;
}BiTNode,*BiTree;

//tag结构体四辅助队列使用的
typedef struct tag{
    BiTree p;//树的某一个结点的地址值
    struct tag *pnext;
}tag_t,*ptag_t;

2、main.cpp文件：

#include "function.h"

//使用递归实现
//前序遍历就是深度优先遍历
void PreOrder(BiTree p)
{
    if(p!=NULL)
    {
        printf("%c",p->c);
        PreOrder(p->lchild);//打印左子树
        PreOrder(p->rchild);//打印右子树
    }
}

//中序遍历
void InOrder(BiTree p)
{
    if(p!=NULL)
    {
        InOrder(p->lchild);//打印左子树
        printf("%c",p->c);
        InOrder(p->rchild);//打印右子树
    }
}

//后序遍历
void PostOrder(BiTree p)
{
    if(p!=NULL)
    {
        PostOrder(p->lchild);//打印左子树
        PostOrder(p->rchild);//打印右子树
        printf("%c",p->c);
    }
}


int main()
{
    BiTree pnew;//用来指向新申请的树结点
    char c;
    BiTree tree=NULL;//tree是指向树根的，代表树
    ptag_t phead=NULL,ptail=NULL,listpnew=NULL,pcur;//phead就是队列头，ptail就是队列尾
    //输入内容为abcdefghij
    while(scanf("%c",&c)) {
        if (c == '\n') {
            break;//读取到换行就结束
        }
        //calloc申请的空间大小是两个参数直接相乘，calloc申请空间并对空间进行初始化，并赋值为0
        pnew = (BiTree) calloc(1, sizeof(BiTNode));
        pnew->c = c;//将数据放进去
        listpnew = (ptag_t) calloc(1, sizeof(tag_t));//给队列结点申请空间
        listpnew->p = pnew;
        //如果是树的第一个结点
        if (NULL == tree) {
            tree = pnew;//tree指向树的根结点
            phead = listpnew;//第一个结点既是队列头也是队列尾
            ptail = listpnew;
            pcur = listpnew;//pcur要指向进入树的父亲元素
        } else {
            //让元素先入队列
            ptail->pnext = listpnew;//新结点放入链表，通过尾插法
            ptail = listpnew;//ptail指向队列尾部
            //接下来把b结点放入树种
            if (NULL==pcur->p->lchild) {
                pcur->p->lchild = pnew;//pcur->左孩子为空，就放入左孩子
            } else if (NULL == pcur->p->rchild) {
                pcur->p->rchild = pnew;//pcur->p右孩子为空，就放入右孩子
                pcur = pcur->pnext;//当前结点左右孩子都有了，pcur就指向下一个
            }
        }
    }
    printf("------PreOrder--------\n");//也叫先序遍历，先打印当前结点，再打印左孩子，最后打印右孩子
    PreOrder(tree);
    printf("\n------InOrder--------\n");//先打印左孩子，再打印当前结点，最后打印右孩子
    InOrder(tree);
    printf("\n------PostOrder--------\n");//先打印左孩子，再打印右孩子,最后打印当前结点
    PostOrder(tree);
    return 0;
}

遍历后结果

四、二叉树的广度优先搜索(BFS)

        层次遍历与层次建树的原理非常类似，层次遍历我们必须使用辅助队列， 为了提高代码的编写效率，我们可以将链表队列中的代码直接拿过来，变为queue.cpp来使用，由于main.cpp和 queue.cpp 都需要使用到对应的结构体类型,所以我们把结构体类型的声明放入functionh头文件,function.h头文件在 main.cpp和 queue.cpp 中都进行了include。

1、function.h文件：

#include <stdio.h>
#include <stdlib.h>

typedef char BiElemType;
typedef struct BiTNode{
    BiElemType c;//就是书籍上的data
    struct BiTNode *lchild;
    struct BiTNode *rchild;
}BiTNode,*BiTree;

//tag结构体四辅助队列使用的
typedef struct tag{
    BiTree p;//树的某一个结点的地址值
    struct tag *pnext;
}tag_t,*ptag_t;

//队列的结构体
typedef BiTree ElemType;
typedef struct LinkNode{
    ElemType data;
    struct LinkNode *next;
}LinkNode;
typedef struct{
    LinkNode *front,*rear;//链表头 链表尾
}LinkQueue;//先进先出
void InitQueue(LinkQueue &Q);
bool IsEmpty(LinkQueue Q);
void EnQueue(LinkQueue &Q,ElemType x);
bool DeQueue(LinkQueue &Q,ElemType &x);

2、main.cpp文件：

#include "function.h"

//使用递归实现
//前序遍历就是深度优先遍历
void PreOrder(BiTree p)
{
    if(p!=NULL)
    {
        printf("%c",p->c);
        PreOrder(p->lchild);//打印左子树
        PreOrder(p->rchild);//打印右子树
    }
}

//中序遍历
void InOrder(BiTree p)
{
    if(p!=NULL)
    {
        InOrder(p->lchild);//打印左子树
        printf("%c",p->c);
        InOrder(p->rchild);//打印右子树
    }
}

//后序遍历
void PostOrder(BiTree p)
{
    if(p!=NULL)
    {
        PostOrder(p->lchild);//打印左子树
        PostOrder(p->rchild);//打印右子树
        printf("%c",p->c);
    }
}

//层次遍历，层序遍历，广度优先遍历
void LevelOrder(BiTree T)
{
    LinkQueue Q;//定义辅助队列
    InitQueue(Q);//初始化队列
    BiTree p;//存储出队的结点
    EnQueue(Q,T);//将树根入队
    while(!IsEmpty(Q))
    {
        DeQueue(Q,p);
        putchar(p->c);//等价于printf("%c",c);
        if(p->lchild)
        {
            EnQueue(Q,p->lchild);//左孩子不为空，就入队左孩子
        }
        if(p->rchild)
        {
            EnQueue(Q,p->rchild);//右孩子不为空，就入队右孩子
        }
    }
}

int main()
{
    BiTree pnew;//用来指向新申请的树结点
    char c;
    BiTree tree=NULL;//tree是指向树根的，代表树
    ptag_t phead=NULL,ptail=NULL,listpnew=NULL,pcur;//phead就是队列头，ptail就是队列尾
    //输入内容为abcdefghij
    while(scanf("%c",&c)) {
        if (c == '\n') {
            break;//读取到换行就结束
        }
        //calloc申请的空间大小是两个参数直接相乘，calloc申请空间并对空间进行初始化，并赋值为0
        pnew = (BiTree) calloc(1, sizeof(BiTNode));
        pnew->c = c;//将数据放进去
        listpnew = (ptag_t) calloc(1, sizeof(tag_t));//给队列结点申请空间
        listpnew->p = pnew;
        //如果是树的第一个结点
        if (NULL == tree) {
            tree = pnew;//tree指向树的根结点
            phead = listpnew;//第一个结点既是队列头也是队列尾
            ptail = listpnew;
            pcur = listpnew;//pcur要指向进入树的父亲元素
        } else {
            //让元素先入队列
            ptail->pnext = listpnew;//新结点放入链表，通过尾插法
            ptail = listpnew;//ptail指向队列尾部
            //接下来把b结点放入树种
            if (NULL==pcur->p->lchild) {
                pcur->p->lchild = pnew;//pcur->左孩子为空，就放入左孩子
            } else if (NULL == pcur->p->rchild) {
                pcur->p->rchild = pnew;//pcur->p右孩子为空，就放入右孩子
                pcur = pcur->pnext;//当前结点左右孩子都有了，pcur就指向下一个
            }
        }
    }
    printf("------PreOrder--------\n");//也叫先序遍历，先打印当前结点，再打印左孩子，最后打印右孩子
    PreOrder(tree);
    printf("\n------InOrder--------\n");//先打印左孩子，再打印当前结点，最后打印右孩子
    InOrder(tree);
    printf("\n------PostOrder--------\n");//先打印左孩子，再打印右孩子,最后打印当前结点
    PostOrder(tree);
    printf("\n------LeverOrder--------\n");
    LevelOrder(tree);
    return 0;
}

3、queue.cpp文件：

#include "function.h"

void InitQueue(LinkQueue &Q)
{
    Q.front=Q.rear=(LinkNode*)malloc(sizeof(LinkNode));//头和尾指向同一个结点
    Q.front->next=NULL;

}

//判断队列是否为空
bool IsEmpty(LinkQueue Q)
{
    return Q.rear==Q.front;
}

//入队
void EnQueue(LinkQueue &Q,ElemType x)
{
    LinkNode *pnew=(LinkNode*)malloc(sizeof(LinkNode));
    pnew->data=x;
    pnew->next=NULL;//要让next为NULL
    Q.rear->next=pnew;//尾指针的next指向pnew，因为从尾部入队
    Q.rear=pnew;//rear要指向新的尾部
}

//出队
bool DeQueue(LinkQueue &Q,ElemType &x)
{
    if(Q.rear==Q.front)//队列为空
    {
        return false;
    }
    LinkNode* q=Q.front->next;//拿到第一个结点,存入q
    x=q->data;//获取要出队的元素值
    Q.front->next=q->next;//让第一个结点断链
    if(Q.rear==q)
    {
        Q.rear=Q.front;//链表只剩余一个结点时，被删除后，要改变rear
    }
    free(q);
    return true;
}

第六章：查找算法

一、顺序查找

顺序查找又称线性查找，它对于顺序表和链表都是适用的。
对于顺序表，可通过数组下标递增来顺序扫描每个元素;
对于链表，则通过指针next 来依次扫描每个元素

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

typedef int ElemType;
typedef struct{
    ElemType* elem;//整型指针，申请的堆空间的起始地址存入elem
    int TableLen;//存储动态数组里面元素的个数
}SSTable;

//初始化顺序表
void ST_Init(SSTable &ST,int len)
{
    //多申请了一个位置，不使用哨兵也可以，但为了和王道书保持一致进行申请
    ST.TableLen = len + 1;
    ST.elem=(ElemType*)malloc(sizeof(ElemType)*ST.TableLen);
    srand(time(NULL));//随机数生成，考研不需要掌握
    int i;
    for(i=0;i<ST.TableLen;i++)//因为第0个是哨兵，所以从1随机
    {
        ST.elem[i]=rand()%100;//为了随机生成的数都在0到99之间
    }
}

//打印顺序表
void ST_print(SSTable ST)
{
    int i;
    for(i=0;i<ST.TableLen;i++)
    {
        printf("%3d",ST.elem[i]);
    }
}

int Search_Seq(SSTable ST,ElemType key)
{
    ST.elem[0]=key;//key存在零号位置，作为哨兵，有了这个，我们在循环时，可以少些一个i>=0判断
    int i;
    for(i=ST.TableLen-1;ST.elem[i]!=key;--i);//从后往前找，找到了，i就是刚好是对应的位置
    return i;
}
//顺序查找
int main() {
    SSTable ST;
    ST_Init(ST,10);//初始化

    ST_print(ST);//打印顺序表中元素
    printf("\n");

    printf("please input search key:\n");
    ElemType key;
    scanf("%d",&key);
    int pos;
    pos = Search_Seq(ST,key);
    if(pos)
    {
        printf("find key ,position=%d\n",pos);
    }else{
        printf("not find\n");
    }
    return 0;
}

二、二分查找（Binary Search）

1、二分查找又称折半查找，它仅适用于有序的顺序表（升序或降序）；

2、折半查找的基本思想:

     首先将给定值key与表中中间位置的元素比较，若相等，则查找成功，返回该元素的存储位置;
    若不等，则所需查找的元素只能在中间元素以外的前半部分或后半部分(例如，在查找表升序排列时，若给定值key大于中间元素，则所查找的元素只可能在后半部分)，
    然后在缩小的范围内继续进行同样的查找,如此重复,直到找到为止,或确定表中没有所需要查找的元素则查找不成功，返回查找失败的信息。

3、针对顺序表有序，我们使用qsort来排序

    1）、qsont 的使用方法如下(qsont初试是不会考这个接口的，机试时会用上，或者复试面试可以讲):

  #include <stdlib.h>
  void qsort( void *buf, size_t num, size t size, int (*compare)(const void *const void *) );

    2）、buf:要排序数组的起始地址，也可以是指针，申请了一块连续的堆空间
    3）、num:数组中元素的个数
    4）、size:数组中每个元素所占用的空间大小
    4）、compare:比较规则，需要我们传递一个函数名，这个函数由我们自己编写返回值必须是 int 类型，形参是两个 void 类型指针，这个函数我们编写，但是是qsort 内部调用的，相当于我们传递一种行为给 qsort。

二分查找动画网址：https://www.cs.usfca.edu/~galles/visualization/Search.html

4、折半查找代码：

折半查找不需要用到哨兵，因此不要受上一节顺序查找的影响，代码实战流程是:
1）、我们初始化顺序表，随机 10个元素
2）、使用 qsont 进行排序，排序完毕后，打印
3）、输人要查找的元素值，存人变量 key中
4）、通过二分查找查找对应key值，找到则输出在顺序表中的位置，没找到输出未找到

核心代码：

int BinarySearch(SSTable L,ElemType key)
{
    int low=0;//初始化左边界为数组起始位置
    int high=L.TableLen-1;//初始化右边界为数组末尾位置
    int mid;
    while(low<=high)//闭区间搜索：允许low=high时继续判断
    {
      mid=(low+high)/2;//计算中间位置
      if(key>L.elem[mid])//目标值在右半区间
      {
          low=mid+1;//调整左边界，排除已检查的mid位置
      }else if(key<L.elem[mid]){//目标值在左半区间
          high=mid-1;//调整右边界，排除已检查的mid位置
      }else{
          return mid;//找到目标值，返回下标
      }
    }
    return -1;//未找到目标值
}

完整代码：

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

typedef int ElemType;
typedef struct {
    ElemType* elem;//整型指针
    int TableLen;//存储动态数组里边元素的个数
}SSTable;

//初始化顺序表
void ST_Init(SSTable &ST,int len)
{
    //多申请了一个位置，不使用哨兵也可以，但为了和王道书保持一致进行申请
    ST.TableLen = len + 1;
    ST.elem=(ElemType*)malloc(sizeof(ElemType)*ST.TableLen);
    srand(time(NULL));//随机数生成，考研不需要掌握
    int i;
    for(i=0;i<ST.TableLen;i++)//因为第0个是哨兵，所以从1随机
    {
        ST.elem[i]=rand()%100;//为了随机生成的数都在0到99之间
    }
}

//打印顺序表
void ST_print(SSTable ST)
{
    int i;
    for(i=0;i<ST.TableLen;i++)
    {
        printf("%3d",ST.elem[i]);
    }
    printf("\n");
}

//实现二分查找
int BinarySearch(SSTable L,ElemType key)
{
    int low=0;
    int high=L.TableLen-1;
    int mid;
    while(low<=high)//low<=high，可以让mid既能取到low，也能取到high
    {
      mid=(low+high)/2;
      if(key>L.elem[mid])//如果目标值大于中位数
      {
          low=mid+1;
      }else if(key<L.elem[mid]){
          high=mid-1;
      }else{
          return mid;
      }
    }
    return -1;
}

//函数名中存储的是函数的额入口地址，也是一个指针，是函数指针类型
//left指针和right指针式指向数组中的任意两个元素
//qsort规定如果left指针指向的值大于right指针指向的值，返回正值；如果小于，返回负值；相等，返回0
int compare(const void *left,const void *right)
{
    return *(int*)left - *(int*)right;
    //return *(ElemType*)right - *(ElemType*)left; //从大到小排序
}

int main() {
    SSTable ST;
    ST_Init(ST,10);//初始化，随机10个元素
    ST_print(ST);
    qsort(ST.elem,ST.TableLen,sizeof(ElemType),compare);//排序
    ST_print(ST);
    ElemType key;
    printf("please input search key:\n");
    scanf("%d",&key);
    int pos=BinarySearch(ST,key);
    if(pos!=-1){
        printf("find key=%d\n",pos+1);
    }else{
        printf("not find\n");
    }
    return 0;
}

三、二叉排序树（BST）

1、二叉排序树(也称二叉查找树)或者是一棵空树，或者是具有下列特性的叉树:

    1）、若左子树非空，则左子树上所有结点的值均小于根结点的值；
    2）、若右子树非空，则右子树上所有结点的值均大于根结点的值；
    3）、左、右子树也分别是一棵二叉排序树。

二叉排序树

二叉排序树动画网址：https://www.cs.usfca.edu/~galles/visualization/BST.html

2、非递归与递归代码实战

        1）、代码流程

        首先我们新建了一颗二叉排序树，然后针对建好的二叉排序树进行了中序遍历输出，接着对二叉排序树进行查找，我们可以看到二叉排序树的最大查找次数是树的高度。

        2）、插入规则：

• 若新节点值小于当前节点，插入左子树。

• 若大于当前节点，插入右子树。

• 若相等，不插入。

        3）、非递归写法：

#include <stdio.h>
#include <stdlib.h>

typedef int KeyType;
typedef struct BSTNode{
    KeyType key;
    struct BSTNode *lchild,*rchild;
}BSTNode,*BiTree;


//进入的元素：54,20,66,40,28,79,58
//非递归的创建二叉查找树
int BST_Insert(BiTree &T,KeyType k)
{
    BiTree TreeNew=(BiTree)calloc(1,sizeof(BSTNode));//新结点申请空间
    TreeNew->key=k;//把值放入
    if(NULL==T)//树为空，新结点作为树的结点
    {
        T=TreeNew;
        return 1;
    }
    BiTree p=T,parent;//p用来查找树
    while(p)
    {
        parent=p;//parent用来存p的父亲
        if(k>p->key)
        {
            p=p->rchild;
        }else if(k<p->key){
            p=p->lchild;
        }else{
            return 0;//相等的元素不可以放入查找树，考研不会考相等元素放入问题
        }
    }
    //接下来要判断放到父亲的左边还是右边
    if(k>parent->key)//大于放到父亲右边
    {
        parent->rchild=TreeNew;
    }else{//小于放到父亲的左边
        parent->lchild=TreeNew;
    }
    return 1;
}

//树中不放相等元素
void Creat_BST(BiTree &T,KeyType *str,int len)
{
    int i=0;
    for(i=0;i<len;i++)
    {
        BST_Insert(T,str[i]);//把某一个结点放入二叉排序树中
    }
}

void InOrder(BiTree T)
{
    if(T!=NULL)
    {
        InOrder(T->lchild);
        printf("%3d",T->key);
        InOrder(T->rchild);
    }
}

BiTree BST_Search(BiTree T,KeyType k,BiTree &parent)
{
    parent=NULL;//存储要找的结点的父亲
    while(T!=NULL && k!=T->key)
    {
        parent=T;
        if(k>T->key)
        {
            T=T->rchild;//比当前节点小，就左边找
        }else{
            T=T->lchild;//比当前节点大，右边去
        }
    }
    return T;
}

//二叉排序树新建，中序遍历，进行查找
int main() {
    BiTree T=NULL;
    KeyType str[7]={54,20,66,40,28,79,58};//将要进入二叉查找树的元素值
    Creat_BST(T,str,7);
    InOrder(T);//中序遍历二叉查找树是由小到大的
    printf("\n");
    BiTree search,parent;
    search= BST_Search(T,40,parent);
    if(search)
    {
        printf("find key %d\n",search->key);
    }else{
        printf("not find\n");
    }
    return 0;
}

        4）、 递归写法：

#include <stdio.h>
#include <stdlib.h>

typedef int KeyType;
typedef struct BSTNode{
    KeyType key;
    struct BSTNode *lchild,*rchild;
}BSTNode,*BiTree;

//进入的元素：54,20,66,40,28,79,58
//非递归的创建二叉查找树
int BST_Insert(BiTree &T,KeyType k)
{
    BiTree TreeNew=(BiTree)calloc(1,sizeof(BSTNode));//新结点申请空间
    TreeNew->key=k;//把值放入
    if(NULL==T)//树为空，新结点作为树的结点
    {
        T=TreeNew;
        return 1;
    }
    BiTree p=T,parent;//p用来查找树
    while(p)
    {
        parent=p;//parent用来存p的父亲
        if(k>p->key)
        {
            p=p->rchild;
        }else if(k<p->key){
            p=p->lchild;
        }else{
            return 0;//相等的元素不可以放入查找树，考研不会考相等元素放入问题
        }
    }
    //接下来要判断放到父亲的左边还是右边
    if(k>parent->key)//大于放到父亲右边
    {
        parent->rchild=TreeNew;
    }else{//小于放到父亲的左边
        parent->lchild=TreeNew;
    }
    return 1;
}

//树中不放相等元素
void Creat_BST(BiTree &T,KeyType *str,int len)
{
    int i=0;
    for(i=0;i<len;i++)
    {
        BST_Insert(T,str[i]);//把某一个结点放入二叉排序树中
    }
}

void InOrder(BiTree T)
{
    if(T!=NULL)
    {
        InOrder(T->lchild);
        printf("%3d",T->key);
        InOrder(T->rchild);
    }
}

//王道书上的递归写法，代码简单，但是理解有难度
int BST_Insert1(BiTree &T,KeyType k){

    if(NULL==T)
    {   //为新节点申请空间，第一个结点作为树根，后面递归再进人的不是树根，是为叶子结点
        T=(BiTree)malloc(sizeof(BSTNode));
        T->key=k;
        T->lchild=T->rchild=NULL;
        return 1;//代表插人成功
    }else if(k==T->key){
        return 0;//发现相同元素，就不插人
    }else if(k<T->key){//如果要插人的结点，小于当前结点
        //函数调用结束后，左孩子和原来的父亲会关联起来，巧妙利用了引用机制
        return BST_Insert1(T->lchild,k);
    }else {
        return BST_Insert1(T->rchild, k);
    }
}

//二叉排序树新建，中序遍历，进行查找
int main() {
    BiTree T=NULL;
    KeyType str[7]={54,20,66,40,28,79,58};//将要进入二叉查找树的元素值
    Creat_BST(T,str,7);
    InOrder(T);//中序遍历二叉查找树是由小到大的
    printf("\n");
    BiTree search,parent;
    search= BST_Search1(T,40,parent);
    if(search)
    {
        printf("find key %d\n",search->key);
    }else{
        printf("not find\n");
    }
    return 0;
}

最终二叉排序树结果

3、二叉排序树删除 

        1）、代码实战步骤:

        在原有二叉树排序树建树，查找的基础上，新增了二叉排序树删除，二叉排序树的删除我们使用递归来实现；

1. 定位到要删除的节点 54：

   1. 通过递归找到 root->key == 54。

2. 处理情况3（左右子树均存在）：

   1. 进入 else 分支。

3. 找到左子树的最大值：

   1. 从 root->lchild = 20 出发，沿着右子树找到最右节点 40。

   2. temp 最终指向 40，parent 指向 20。

4. 替换值：

   1. 将 root->key（54）替换为 temp->key（40）。

   2. 此时树结构变为：

            40
          /   \
         20    66
          \   /  \
          40 58  79
          /
         28

5. 调整指针：

   1. parent（20）的右孩子原本指向 40，现在将其指向 40 的左子树（28）。

   2. 调整后结构：

            40
          /   \
         20    66
          \   /  \
          28 58  79

二叉排序树的删除动画网址：https://www.cs.usfca.edu/~galles/visualization/BST.html

        2）、删除二叉查找树节点需要处理三种情况：

• 叶子节点：直接删除。
• 仅一个子节点：用子节点替换当前节点。
• 有两个子节点：找到左子树的最大节点或右子树的最小节点替换当前节点。

        3）、二叉排序树删除代码：

#include <stdio.h>
#include <stdlib.h>

typedef int KeyType;
typedef struct BSTNode{
    KeyType key;
    struct BSTNode *lchild,*rchild;
}BSTNode,*BiTree;

//王道书上的递归写法，代码简单，但是理解有难度
int BST_Insert(BiTree &T,KeyType k){
    if(NULL==T)
    {   //为新节点申请空间，第一个结点作为树根，后面递归再进人的不是树根，是为叶子结点
        T=(BiTree)malloc(sizeof(BSTNode));
        T->key=k;
        T->lchild=T->rchild=NULL;
        return 1;//代表插人成功
    }else if(k==T->key){
        return 0;//发现相同元素，就不插人
    }else if(k<T->key){//如果要插人的结点，小于当前结点
        //函数调用结束后，左孩子和原来的父亲会关联起来，巧妙利用了引用机制
        return BST_Insert(T->lchild,k);
    }else {
        return BST_Insert(T->rchild, k);
    }
}

//树中不放相等元素
void Creat_BST(BiTree &T,KeyType *str,int len)
{
    int i=0;
    for(i=0;i<len;i++)
    {
        BST_Insert(T,str[i]);//把某一个结点放入二叉排序树中
    }
}

void InOrder(BiTree T)
{
    if(T!=NULL)
    {
        InOrder(T->lchild);
        printf("%3d",T->key);
        InOrder(T->rchild);
    }
}

BiTree BST_Search(BiTree T,KeyType k,BiTree &parent)
{
    parent=NULL;//存储要找的结点的父亲
    while(T!=NULL && k!=T->key)
    {
        parent=T;
        if(k>T->key)
        {
            T=T->rchild;//比当前节点小，就左边找
        }else{
            T=T->lchild;//比当前节点大，右边去
        }
    }
    return T;
}

//这个书上没有二叉排序树删除代码---考大题没那么高概率
void DeleteNode(BiTree &root,KeyType x)
{
    if(root==NULL)
    {
        return;
    }
    if(root->key>x)//当前结点大于要删除的结点，往左子树找
    {
        DeleteNode(root->lchild,x);
    }else if(root->key<x){//当前结点小于要删除的结点，往右子树找
        DeleteNode(root->rchild,x);
    }else{//找到了要删除的结点
        if(root->lchild==NULL)//左子树为空，右子树直接顶上去
        {
            BiTree tempNode=root;//临时指针存储当前结点，用临时指针存储的目的是一会要free
            root = root->rchild;
            free(tempNode);
        }else if(root->rchild==NULL){//右子树为空，左子树直接顶上去
            BiTree tempNode=root;//临时指针存储当前结点
            root = root->lchild;
            free(tempNode);
        }else{//左右子树均都不为空
            //一般的删除策略是找左子树的最大数据 或 右子树的最小数据，代替要删除的结点（这里要采用查找左子树最大数据来代替，也就是左子树的最右结点）
            BiTree parentNode = root;
            BiTree tempNode=root->lchild;
            while(tempNode->rchild!=NULL)
            {
                parentNode = tempNode;
                tempNode = tempNode->rchild;
            }
            root->key = tempNode->key;//把 tempNode 对应的值替换到要删除的值的位置上
            if(parentNode->lchild==tempNode)//判断tempNode是父亲的左孩子还是右孩子
            {
                parentNode->lchild=tempNode->lchild;
            }else{
                parentNode->rchild=tempNode->lchild;
            }
            free(tempNode);
            //DeleteNode(root->lchild,tempNode->key);//在左子树中找到tempNode的值并删除tempNode
        }
    }
}



//二叉排序树新建，中序遍历，进行查找
int main() {
    BiTree T=NULL;
    KeyType str[7]={54,20,66,40,28,79,58};//将要进入二叉查找树的元素值
    Creat_BST(T,str,7);
    InOrder(T);//中序遍历二叉查找树是由小到大的
    printf("\n");
    BiTree search,parent;
    search= BST_Search(T,40,parent);
    if(search)
    {
        printf("find key %d\n",search->key);
    }else{
        printf("not find\n");
    }

    //实现二叉排序树的删除
    DeleteNode(T,54);//删除某个节点
    InOrder(T);
    printf("\n");
    return 0;
}

第七章：排序算法

一、冒泡排序（Bubble Sort）

1、排序算法分为交换类排序，插入类排序，选择类排序，归并类排序

2、交换排序分为：

1）、冒泡排序

2）、快速排序

3、冒泡排序（冒泡排序考研中一般考选择题，考大题概率较低）：

（1）、冒泡排序的基本思想是:
        从后往前(或从前往后)两两比较相邻元素的值，(若A[j-1]>A])，则交换它们，直到序列比较完。我们称它为第一趟冒泡，结果是将最小的元素交换到待排序列的第一个位置。关键字最小的元素如气泡一般逐渐往上“漂浮”直至“水面”。下一趟冒泡时前一趟确定的最小元素不再参与比较，每趟冒泡的结果是把序列中的最小元素放到了序列的最终位置.……..这样最多做n-1趟冒泡就能把所有元素排好序。
冒泡排序动画网址：https://www.cs.usfca.edu/~galles/visualization/ComparisonSort.html

 4、代码实战步骤:

        首先我们通过随机数生成10个元素，通过随机数生成，我们可以多次测试排序算法是否正确，然后打印随机生成后的元素顺序，然后通过冒泡排序对元素进行排序，然后再次打印排序后的元素顺序；

核心代码：

void BubbleSort(ElemType *A,int n)
{
    int i,j;
    bool flag;
    for(i=0;i<n-1;i++)//控制排序轮数，每轮确定一个最大值到右侧有序区
    {
        flag=false;
        for(j=n-1;j>i;j--)//从后向前遍历，将较小元素“冒泡”到左侧无序区
        {
            if(A[j-1]>A[j])
            {
                swap(A[j-1],A[j]);
                flag=true;
            }
        }
        
    }
    if(false==flag)
    {
        return;
    }
}

完整代码：

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <string.h>

typedef int ElemType;
typedef struct{
    ElemType *elem;//存储元素的起始地址
    int TableLen;//元素个数
}SSTable;

void ST_Init(SSTable &ST, int len)
{
    ST.TableLen = len;
    ST.elem = (ElemType *) malloc(sizeof(ElemType)*ST.TableLen);//申请一块堆空间，当数组来使用int i;
    int i;
    srand(time(NULL));//随机数生成，每一次执行代码就会得到随机的 10个元素
    for(i=0;i<ST.TableLen;i++)
    {
        ST.elem[i]=rand()%100;//生成的是 0-99之间
    }
}

//打印数组中的元素
void ST_print(SSTable ST)
{
    for (int i=0; i < ST.TableLen;i++)
    {
        printf("%3d", ST.elem[i]);
    }
    printf("\n");
}

//交换两个元素
void swap(int &a,int &b)
{
    ElemType tmp;
    tmp=a;
    a=b;
    b=tmp;
}

//往往都是使用两层循环的
//有限去写内层循环，再去写外层循环
void BubbleSort(ElemType *A,int n)
{
    int i,j;
    bool flag;
    for(i=0;i<n-1;i++)//外层循环控制的是有序数的数目
    {
        for(j=n-1;j>i;j--)//内层循环控制比较和交换
        {
            if(A[j-1]>A[j])
            {
                swap(A[j-1],A[j]);
                flag=true;
            }
        }
    }
    if(false==flag)
    {
        return;
    }
}

int main() {
    SSTable ST;
    ST_Init(ST,10);//初始化
    ElemType A[10]={64,94,95,79,69,84,18,22,12,78};
    //内存 copy接口,当你 copy整型数组,或者浮点型时,要用memcpy,不能用 strcpy,初试考 memcpy概率很低
    memcpy(ST.elem,A,sizeof(A));//这是为了降低调试难度，每次数组数据固定而设计的
    ST_print(ST);//随机后的结果打印
    BubbleSort(ST.elem,10);
    ST_print(ST);
    return 0;
}

5、时间复杂度与空间复杂度：

        时间复杂度其实就是程序实际的运行次数，可以看到内层是>i，外层i的值是从0到N-1，所以程序的总运行次数是1+2+3+…+(N-1)，即从1 一直加到N-1，这是等差数列求和，得到的结果是N(N-1)/2，即总计运行了这么多次，忽略了低阶项和高阶项的首项系数，因为时间复杂度为(㎡)。因为未使用额外的空间(额外空间必须与输入元素的个数 N相关)，所以空间复杂度为 (1)如果数组本身有序，那么就是最好的时间复杂度 (n).

二、快速排序（Quick Sort）

1、快速排序的核心是分治思想（快速排序，简称快排，快排在考研初试中出大题的概率很高，也会出选择题，所以非常重要!）:

        分治思想（Divide and Conquer）是一种通过分解问题、解决子问题、合并结果来解决复杂问题的策略。其核心可概括为：

• 分解：将大规模问题拆分为多个相互独立且形式相同的子问题（如将蛋糕切成小块）；
• 解决：递归或直接处理子问题（当子问题足够简单时直接求解）；
• 合并：将子问题的解整合为原问题的解（如拼合小蛋糕块还原整体）。

        假设我们的目标依然是按从小到大的顺序排列，我们找到数组中的一个分割值，把比分割值小的数都放在数组的左边，把比分割值大的数都放在数组的右边，这样分割值的位置就被确定数组一分为二，我们只需排前一半数组和后一半数组，复杂度直接减半。采用这种思想不断地进行递归，最终分割得只剩一个元素时，整个序列自然就是有序的。

2、代码实战步骤:

        首先我们通过随机数生成10个元素，通过随机数生成，我们可以多次测试排序算法是否正确，然后打印随机生成后的元素顺序，然后通过快速排序对元素进行排序，然后再次打印排序后的元素顺序。

3、假如每次快速排序数组都被平均地一分为二：

        那么可以得出 QuickSont递归的次数是 log2n,第一次 partition遍历次数为n，分成两个数组后，每个数组遍历n/2次，加起来还是n，因此时间复杂度是 (nog2n)，因为计算机是二进制的，所以在复试面试回答复杂度或与人交流时，提到复杂度时一般直接讲 O(nlogn)，而不带下标。

 核心代码：

int partition(ElemType *A,int low,int high)
{
    ElemType pivot=A[low];//选择最左端元素作为枢轴（基准值）
    while(low<high)//双指针向中间移动，直到相遇
    {
        while(low<high && A[high]>=pivot)// 从右向左找第一个小于pivot 的元素
        {
            high--;
        }
        A[low]=A[high];//将小元素移到左侧“坑位”
        while(low<high && A[low]<=pivot) 从左向右找第一个大于pivot 的元素
        {
            low++;
        }
        A[high]=A[low];//将大元素移到右侧“坑位”
    }
    A[low]=pivot;//枢轴归位，此时左侧小于等于pivot，右侧大于等于pivot
    return low;//返回枢轴最终位置
}

void QuickSort(ElemType *A,int low,int high)
{
    if(low<high)//递归终止条件：子数组长度大于等于1
    {
        int pivot_pos=partition(A,low,high);//划分数组并获取枢轴位置
        QuickSort(A,low,pivot_pos-1);//递归排序左半部分
        QuickSort(A,pivot_pos+1,high);//递归排序右半部分
    }

}

 完整代码：

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

typedef int ElemType;
typedef struct{
    ElemType *elem;//存储元素的起始地址
    int TableLen;//元素个数
}SSTable;

void ST_Init(SSTable &ST, int len)
{
    ST.TableLen = len;
    ST.elem = (ElemType *) malloc(sizeof(ElemType)*ST.TableLen);//申请一块堆空间，当数组来使用int i;
    int i;
    srand(time(NULL));//随机数生成，每一次执行代码就会得到随机的 10个元素
    for(i=0;i<ST.TableLen;i++)
    {
        ST.elem[i]=rand()%100;//生成的是 0-99之间
    }
}

//打印数组中的元素
void ST_print(SSTable ST)
{
    for (int i=0; i < ST.TableLen;i++)
    {
        printf("%3d", ST.elem[i]);
    }
    printf("\n");
}

//64 94 95 79 69 84 18 22 12 78
//比 64 小的放在左边，比64 大的放在右边
//partition（分隔）快排的核心函数,使用的快排方法是挖坑法
int partition(ElemType *A,int low,int high)
{
    ElemType pivot=A[low];//将最左边的值作为分隔值，并存储下来
    while(low<high)
    {
        while(low<high && A[high]>=pivot)//从后往前遍历，找到一个比分隔值小的元素
        {
            high--;
        }
        A[low]=A[high];//把比分隔值小的那个元素放到A[low]中
        while(low<high && A[low]<=pivot)//从后往前遍历，找到一个比分隔值大的元素
        {
            low++;
        }
        A[high]=A[low];//把比分隔值大的那个元素放到A[high]中，放到A[high]，因为刚才high位置的元素已经放到了low的位置
    }
    A[low]=pivot;//把分隔值放到中间位置，因为左边刚好都比它小，右边的都比它大
    return low;//返回分隔值所在的下表
}

//递归实现
void QuickSort(ElemType *A,int low,int high)
{
    if(low<high)
    {
        int pivot_pos=partition(A,low,high);//pivot（中心）用来存储分隔值的位置
        QuickSort(A,low,pivot_pos-1);//前一半继续递归排好
        QuickSort(A,pivot_pos+1,high);//接着后一半递归排好
    }

}

int main() {
    SSTable ST;
    ST_Init(ST,10);//初始化
    //ElemType A[10]={64,94,95,79,69,84,18,22,12,78};
    //内存 copy接口,当你 copy整型数组,或者浮点型时,要用memcpy,不能用 strcpy,初试考 memcpy概率很低
    //memcpy(ST.elem,A,sizeof(A));//这是为了降低调试难度，每次数组数据固定而设计的
    ST_print(ST);//随机后的结果打印
    QuickSort(ST.elem,0,9);
    ST_print(ST);
    return 0;
}

4、快速排序最差的时间复杂度为什么是n2呢?

        因为数组本身从小到大有序时，如果每次我们仍然用最左边的数作为分割值,那么每次数组都不会二分，导致递归n次，所以快速排序最坏时间复杂度为n的平方，当然，为了避免这种情况有时会首先随机选择一个下标，先将对应下标的值与最左边的元素交换，再进行partition 操作从而极大地降低出现最坏时间复杂度的概率，但是仍然不能完全避免因此快排最好和平均时间复杂度是 O(nlog2n)，最差是 O(n2)。

5、快排的空间复杂度是 O(log2n)，因为递归的次数是log2n，而每次递归的形参都是需要占用空间的。

三、插入排序（Insertion Sort）

1、插入排序分为

1）、直接插入排序

2）、折半插人排序

3）、希尔排序
    以上3种插入类型的排序，考研都是考选择题，考大题概率很低，因此我们仅讲解直接插人排序的原理与代码实战，折半插入排序与希尔排序原理可以在后面的408课程中进行学习。

2、如果一个序列只有一个数，那么该序列自然是有序的。

                插入排序首先将第一个数视为有序序列，然后把后面9个数视为要依次插人的序列。首先，我们通过外层循环控制要插人的数，用insertVal保存要插入的值 87，我们比较 an[0]是否大于ar[1]，即3是否大于 87，由于不大于，因此不发生移动，这时有序序列是3,87；

        接着，将数值2插人有序序列，首先将2 赋给 insertVal，这时判断87 是否大于 2，因为87 大于2，所以将87 向后移动,将2 覆盖然后判断3是否大于2，因为3大于2，所以3移动到87 所在的位置， 内层循环结束，这时将2赋给 arr[0]的位置，得到下表中第2次插入后的效果。 继续循环会将数依次插人有序序列，最终使得整个数组有序.插人排序主要用在部分数有序的场景， 例如手机通讯录时时刻刻都是有序的,新增一个电话号码时，以插入排序的方法将其插入原有的有序序列，这样就降低了复杂度。

插入排序动画网址：https://www.cs.usfca.edu/~galles/visualization/ComparisonSort.html

3、代码实战步骤：

        随机10个元素，然后打印，接着进行插入排序，然后打印排序后结果。

核心代码：

void InsertionSort(ElemType *A,int n)
{
    int i,j,insertVal;
    for(i=1;i<n;i++)//外层循环：遍历未排序元素
    {
        insertVal=A[i];//保存当前待插入值
        for(j=i-1;j>=0 && A[j]>insertVal;j--)//内层循环：寻找插入位置并腾出空间,j>=0保持数组不能越界
        {
            A[j+1]=A[j];//当前j位置的元素后移一位，腾出空间
        }
        A[j+1]=insertVal;//插入元素到正确位置
    }
}

完整代码：

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

typedef int ElemType;
typedef struct{
    ElemType *elem;//存储元素的起始地址
    int TableLen;//元素个数
}SSTable;

void ST_Init(SSTable &ST, int len)
{
    ST.TableLen = len;
    ST.elem = (ElemType *) malloc(sizeof(ElemType)*ST.TableLen);//申请一块堆空间，当数组来使用int i;
    int i;
    srand(time(NULL));//随机数生成，每一次执行代码就会得到随机的 10个元素
    for(i=0;i<ST.TableLen;i++)
    {
        ST.elem[i]=rand()%100;//生成的是 0-99之间
    }
}

//打印数组中的元素
void ST_print(SSTable ST)
{
    for (int i=0; i < ST.TableLen;i++)
    {
        printf("%3d", ST.elem[i]);
    }
    printf("\n");
}

void InsertionSort(ElemType *A,int n)
{
    int i,j,insertVal;
    for(i=1;i<n;i++)//外层要控制要插入的数
    {
        insertVal=A[i];//先保存要插入的值
        for(j=i-1;j>=0 && A[j]>insertVal;j--)//内层控制比较，j要大于等于0，同时A[j]大于insertVal时，A[j]位置元素往后覆盖。
        {
            A[j+1]=A[j];
        }
        A[j+1]=insertVal;//把要插入的元素放入对应的位置
    }
}

int main() {
    SSTable ST;
    ST_Init(ST,10);//初始化
    ST_print(ST);//随机后的结果打印
    InsertionSort(ST.elem,10);
    ST_print(ST);
    return 0;
}

4、时间复杂度与空间复杂度：

        随着有序序列的不断增加，插人排序比较的次数也会增加，插人排序的执行次数也是从1加到N-1，总运行次数为N(N-1)/2，时间复杂度依然为O(n2），因为未使用额外的空间(额外空间必须与输入元素的个数 N相关)，所以空间复杂为(1)；如果数组本身有序，那么就是最好的时间复杂度 O(n)。当数组有序，我们的内层循环每次都是无法进入的，因此，最好的时间复杂度就是 O(n).

四、选择排序（Selection Sort）

1、选择排序分为

• 简单选择排序
•  堆排序(重要)

2、简单选择排序原理:

        假设排序表为L[1…n，第i趟排序即从Li…n]中选择关键字最小的元素与 L(0)交换，每一趟排序可以确定一个元素的最终位置，这样经过n-1趟排序就可使得整个排序表有序.

        首先假定第零个元素是最小的，把下标0赋值给min(min 记录最小的元素的下标)，内层比较时，从1号元素一直比较到9号元素，谁更小，就把它的下标赋给min，一轮比较结束后，将min 对应位置的元素与元素i交换，如下表所示。第一轮确认2最小，将2与数组开头的元素3交换。第二轮我们最初认为87最小，经过一轮比较，发现3最小，这时将87与3交换，持续进行最终使数组有序。

选择排序动画网址：https://www.cs.usfca.edu/~galles/visualization/ComparisonSort.html

3、代码实战步骤：

        是随机10个元素，然后打印，接着进行选择排序，然后打印排序后结果

• 原理：
  •  每一轮从未排序部分选择最小元素。
  • 将其与未排序部分的第一个元素交换。 
• 流程：
  • 外层循环 i 控制轮数（共 n-1 轮）。
  • 内层循环 j 遍历未排序部分，找到最小值下标 min。
  • 如果 min 不是初始的 i，则交换位置。

核心代码：

void SelectSort(ElemType* A,int n)
{
    int i,j,min;
    for(i=0;i<n-1;i++)//外层循环：控制已排序部分的边界
    {
        min=i;//假设当前i位置的元素是未排序部分的最小值
        for(j=i+1;j<n;j++)//内层循环：遍历未排序部分，查找实际最小值的位置
        {
            if(A[j]<A[min])//发现更小的元素
            {
                min=j;//更新最小值下标
            }
        }
        if(min!=i)//如果最小值不在当前位置i，则交换
        {
            swap(A[i],A[min]);//将最小值交换到已排序部分的末尾
        }
    }
}

完整代码：

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <string.h>

typedef int ElemType;
typedef struct{
    ElemType *elem;//存储元素的起始地址
    int TableLen;//元素个数
}SSTable;

void ST_Init(SSTable &ST, int len)
{
    ST.TableLen = len;
    ST.elem = (ElemType *) malloc(sizeof(ElemType)*ST.TableLen);//申请一块堆空间，当数组来使用int i;
    srand(time(NULL));//随机数生成，每一次执行代码就会得到随机的 10个元素
    int i;
    for(i=0;i<ST.TableLen;i++)
    {
        ST.elem[i]=rand()%100;//生成的是 0-99之间
    }
}

//打印数组中的元素
void ST_print(SSTable ST)
{
    for (int i=0; i < ST.TableLen;i++)
    {
        printf("%3d", ST.elem[i]);
    }
    printf("\n");
}

//交换两个元素
void swap(int &a,int &b)
{
    ElemType tmp;
    tmp=a;
    a=b;
    b=tmp;
}

void SelectSort(ElemType* A,int n)
{
    int i,j,min;
    for(i=0;i<n-1;i++)
    {
        min=i;//我们认为i号元素最小
        for(j=i+1;j<n;j++)//找到从i开始到最后的序列的最小值的下标,j最多可以为9
        {
            if(A[j]<A[min])//当某个元素A[j]小于最小元素A[min]
            {
                min=j;//将下标j赋值给min，min就记录下来了最小值的下标
            }
        }
        if(min!=i)
        {
            swap(A[i],A[min]);//遍历完毕找到最小值的位置后，与A[i]交换，这样最小值被放到了最前面
        }
    }
}

int main() {
    SSTable ST;
    ST_Init(ST,10);//初始化
    //下面两行代码是为了降低调试难度，每次数组数据固定而设计的
    //ElemType A[10]={64,94,95,79,69,84,18,22,12,99};
    //memcpy(ST.elem,A,sizeof(A));
    ST_print(ST);
    SelectSort(ST.elem,10);
    ST_print(ST);
    return 0;
}

4、时间复杂度与空间复杂度：

        选择排序虽然减少了交换次数，但是循环比较的次数依然和冒泡排序的数量是一样的，都是从1加到N-1，总运行次数为N(N-1)/2.我们忽略循环内语句的数量，因为我们在计算时间复杂度时，主要考虑与N有关的循环，如果循环内交换得多,例如有5条语句，那么最终得到的无非是5n2;循环内交换得少， 例如有2条语句，那么得到的就是2n2，但是时间复杂度计算是忽略首项系数的，因此最终还是O(n2).因此，选择排序的时间复杂度依然为O(n2).因为未使用额外的空间(额外空间必须与输入元素的个数N 相关)，所以空间复杂为O(1)。

        另外考研初试问时间复杂度直接写最终结果即可，不用分析过程，除非清晰说明需要给出计算过程，或者分析过程(但是目前一直都没有这个要求)

五、堆排序（Heap Sort）

1、堆(Heap)是计算机科学中的一种特殊的树状数据结构：

        若满足以下特性，则可称为堆:“给定堆中任意结点P和C若P是C的父结点，则P的值小于等于(或大于等于)C的值。” 若父结点的值恒小于等于子结点的值，则该堆称为最小堆(min heap);反之，若父结点的值恒大于等于子结点的值，则该堆称为最大堆(max heap)。堆中最顶端的那个结点称为根结点(rootnode)，根结点本身没有父结点(parentnode)。平时在工作中，我们将最小堆称为小根堆或小顶堆，把最大堆称为大根堆或大顶堆，

2、假设我们有3,87,2,93,78,56,61,38,12,40共10个元素我们将这10个元素建成一棵完全二叉树

        这里采用层次建树法，虽然只用一个数组存储元素，但是我们能将二叉树中任意一个位置的元素对应到数组下标上，我们将二叉树中每个元素对应到数组下标的这种数据结构称为堆，比如最后一个父元素的下标是N/2-1，也就是a[41，对应的值为78为什么是N/2-1?因为这是层次建立一棵完全二叉树的特性。 可以这样记忆:如果父结点的下标是dad，那么父结点对应的左子结点的下标值是2*dad+1。接着，依次将每棵子树都调整为父结点最大，最终将整棵树变为一个大根堆。

堆排序动画网址：https://www.cs.usfca.edu/~galles/visualization/HeapSort.html

 除了快排，接着就是堆排会在初试中出大题，也会出选择题，所以重要! 

3、代码实战步骤:

        首先我们通过随机数生成10个元素，通过随机数生成，我们可以多次测试排序算法是否正确，然后打印随机生成后的元素顺序，然后通过堆排序对元素进行排序，然后再次打印排序后的元素顺序。
    堆排序的步骤是首先把堆调整为大根堆,然后我们交换根部元素也就是 A[0]和最后一个元素,这样最大的元素就放到了数组最后，接着我们将剩余9个元素继续调整为大根堆,然后交换 A[0]和9个元素的最后一个,循环往复,直到有序。

核心代码：

void AdjustDown1(ElemType A[],int k,int len)
{
    int dad=k;//父亲的下标
    int son=2*dad+1;//左孩子的下标
    while(son<len)
    {
        if(son+1<len && A[son]<A[son+1])//如果左孩子小于右孩子
        {
            son++;//拿右孩子
        }
        if(A[son]>A[dad])//比较孩子和父亲，如果孩子大于父亲，那么就进行交换
        {
            swap(A[son],A[dad]);//孩子和父亲进行交换
            dad=son;//son重新作为dad去判断下面的字数是否符合大根堆
            son=2*dad+1;
        }else{
            break;
        }
    }
}

void HeapSort1(ElemType A[],int len)
{
    int i;
    //就是把堆调整为大根堆
    for(i=len/2-1;i>=0;i--)
    {
        AdjustDown1(A,i,len);
    }
    swap(A[0],A[len-1]);//交换根部元素和最后一个元素
    for(i=len-1;i>1;i--)//i代表的是剩余的无序数的数组的长度
    {
        AdjustDown1(A,0,i);//调整说呢过于元素变为大根堆
        swap(A[0],A[i-1]);//交换根部元素和无序树的数组的最后一个元素
    }
}

完整代码：

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <string.h>

typedef int ElemType;
typedef struct{
    ElemType *elem;//存储元素的起始地址
    int TableLen;//元素个数
}SSTable;

void ST_Init(SSTable &ST, int len)
{
    ST.TableLen = len;
    ST.elem = (ElemType *) malloc(sizeof(ElemType)*ST.TableLen);//申请一块堆空间，当数组来使用int i;
    srand(time(NULL));//随机数生成，每一次执行代码就会得到随机的 10个元素
    int i;
    for(i=0;i<ST.TableLen;i++)
    {
        ST.elem[i]=rand()%100;//生成的是 0-99之间
    }
}

//打印数组中的元素
void ST_print(SSTable ST)
{
    for (int i=0; i < ST.TableLen;i++)
    {
        printf("%3d", ST.elem[i]);
    }
    printf("\n");
}

//交换两个元素
void swap(int &a,int &b)
{
    ElemType tmp;
    tmp=a;
    a=b;
    b=tmp;
}

//王道书上调整某个父亲节点
void AdjustDown(ElemType A[],int k,int len)
{
    int i;
    A[0]=A[k];
    for(i=2*k;i<=len;i*=2) {
        if (i < len && A[i] < A[i + 1])//左子节点与右子节点比较大小
        i++;
        if (A[0] >= A[i])
            break;
        else {
            A[k] = A[i];
            k = i;
        }
    }
    A[k]=A[0];
}

void BuildMaxHeap(ElemType A[],int len)
{
    for(int i=len/2;i>0;i--)
    {
        AdjustDown(A,i,len);
    }
}

//王道树上的堆排序
void HeapSort(ElemType A[],int len)
{
    int i;
    BuildMaxHeap(A,len);
    for(i=len;i>1;i--)
    {
        swap(A[i],A[1]);
        AdjustDown(A,1,i-1);
    }
}

//将某个子树调整为大根堆
void AdjustDown1(ElemType A[],int k,int len)
{
    int dad=k;//父亲的下标
    int son=2*dad+1;//左孩子的下标
    while(son<len)
    {
        if(son+1<len && A[son]<A[son+1])//如果左孩子小于右孩子
        {
            son++;//拿右孩子
        }
        if(A[son]>A[dad])//比较孩子和父亲，如果孩子大于父亲，那么就进行交换
        {
            swap(A[son],A[dad]);//孩子和父亲进行交换
            dad=son;//son重新作为dad去判断下面的字数是否符合大根堆
            son=2*dad+1;
        }else{
            break;
        }
    }
}

void HeapSort1(ElemType A[],int len)
{
    int i;
    //就是把堆调整为大根堆
    for(i=len/2-1;i>=0;i--)
    {
        AdjustDown1(A,i,len);
    }
    swap(A[0],A[len-1]);//交换根部元素和最后一个元素
    for(i=len-1;i>1;i--)//i代表的是剩余的无序数的数组的长度
    {
        AdjustDown1(A,0,i);//调整说呢过于元素变为大根堆
        swap(A[0],A[i-1]);//交换根部元素和无序树的数组的最后一个元素
    }
}

int main() {
    SSTable ST;
    ST_Init(ST,10);//初始化
    //ElemType A[10]={3,87,2,93,78,56,61,38,12,40};
    //memcpy(ST.elem,A,sizeof(A));
    ST_print(ST);
    HeapSort1(ST.elem,10);
    ST_print(ST);

    HeapSort(ST.elem,9);
    ST_print(ST);
    return 0;
}

4、时间复杂度与空间复杂度：

        AdjustDown1 函数的循环次数是logzn，HeapSortl函数的第一个for循环了n2 次，第二个for 循环了n次，总计次数是 3/2nlogen 次，因此时间复杂度是O(nlogzn).堆排最好、最坏、平均时间复杂度都是 O(nlogzn)；

        堆排的空间复杂度是 O(1)，因为没有使用与n相关的额外空间。

六、归并排序（Merge sort）

1、如上图所示

        我们把每两个元素归为一组，进行小组内排序，然后再次把两个有序小组合并为一个有序小组，不断进行，最终合并为一个有序数组。

归并排序动画网址：https://www.cs.usfca.edu/~galles/visualization/ComparisonSort.html

 2、代码实战步骤：

        归并排序是一种经典的分治算法，其核心思想是将一个大问题分解为多个小问题，分别解决这些小问题，然后将小问题的解合并起来得到大问题的解。

        首先，最小下标值和最大下标值相加并除以 2，得到中间下标值mid，用MergeSort对low到mid 排序，然后用MergeSort对 mid+1到high排序，当数组的前半部分和后半部分都排好序后，使用Merge 函数.Merge函数的作用是合并两个有序数组。为了提高合并有序数组的效率，在Merge函数内定义了 B[N]。首先，我们通过循环把数组A中从low到high的元素全部复制到B中，这时游标i(遍历的变量称为游标)从low开始，游标j从mid+1开始，谁小就将谁先放人数组A对其游标加 1，并在每轮循环时对数组的计数游标k加1。

        

核心代码：

这段代码主要包含两个函数：Merge 函数和 MergeSort 函数。

• Merge 函数的作用是将两个有序数组合并成一个有序数组;

• 代码解释：

  • static ElemType B[N];：定义一个静态数组 B，用于临时存储数组 A 的元素。使用 static 关键字的目的是确保无论递归调用多少次 Merge 函数，都只有一个 B[N] 数组，避免重复创建数组，节省内存。
  • for(k = low; k <= high; k++)：将数组 A 中从下标 low 到 high 的元素复制到数组 B 中。
  • for(i = low, j = mid + 1, k = i; i <= mid && j <= high; k++)：合并两个有序子数组 B[low...mid] 和 B[mid+1...high]。比较 B[i] 和 B[j] 的大小，将较小的元素放入数组 A[k] 中，并将相应的指针后移。
  • while(i <= mid) 和 while(j <= high)：处理剩余的元素。如果其中一个子数组已经遍历完，将另一个子数组中剩余的元素直接复制到数组 A 中。

• MergeSort 函数则是利用分治思想对数组进行递归排序。

• 代码解释：

  • if(low < high)：判断数组是否至少有两个元素。如果只有一个元素或者没有元素，则不需要排序。
  • int mid = (low + high) / 2;：计算数组的中间位置。
  • MergeSort(A, low, mid);：递归调用 MergeSort 函数，对数组的前一半进行排序。
  • MergeSort(A, mid + 1, high);：递归调用 MergeSort 函数，对数组的后一半进行排序。
  • Merge(A, low, mid, high);：调用 Merge 函数，将两个排序好的子数组合并成一个有序数组。

void Merge(ElemType A[],int low,int mid,int high)
{
    static ElemType B[N];//加static的目的是无论递归调用多少次，都只有一个B[N]
    int i,j,k;
    for(i=low;i<=high;i++)//把A[i]里面的元素都给B[i]
    {
        B[i]=A[i];
    }
    for(i=low,j=mid+1,k=i;i<=mid && j<=high;)//合并两个有序数组
    {
        if(B[i]<=B[j]){
            A[k]=B[i++];
            k++;
        }else{
            A[k]=B[j++];
            k++;
        }
    }
    //把某一个有序数组中剩余的元素放进来
    while(i<=mid)//前一半的有剩余的放入
    {
        A[k]=B[i++];//后一半的有剩余的放入
        k++;
    }
    while(j<=high)
    {
        A[k]=B[j++];
        k++;
    }
}

//归并排序不限制是两两归并，还是多个归并，但是考研一般都是考两两归并
void MergeSort(ElemType A[],int low,int high)
{
    if(low<high)
    {
        int mid=(low+high)/2;
        MergeSort(A,low,mid);//排序好前一半
        MergeSort(A,mid+1,high);//排序好后一半
        Merge(A,low,mid,high);//将两个排序好的数组合并
    }
}

完整代码：

#include <stdio.h>

#define N 7
typedef int ElemType;

//合并两个有序数组
void Merge(ElemType A[],int low,int mid,int high)
{
    static ElemType B[N];//加static的目的是无论递归调用多少次，都只有一个B[N]
    int i,j,k;
    for(i=low;i<=high;i++)//把A[i]里面的元素都给B[i]
    {
        B[i]=A[i];
    }
    for(i=low,j=mid+1,k=i;i<=mid && j<=high;)//合并两个有序数组
    {
        if(B[i]<=B[j]){
            A[k]=B[i++];
            k++;
        }else{
            A[k]=B[j++];
            k++;
        }
    }
    //把某一个有序数组中剩余的元素放进来
    while(i<=mid)//前一半的有剩余的放入
    {
        A[k]=B[i++];//后一半的有剩余的放入
        k++;
    }
    while(j<=high)
    {
        A[k]=B[j++];
        k++;
    }
}

//归并排序不限制是两两归并，还是多个归并，但是考研一般都是考两两归并
void MergeSort(ElemType A[],int low,int high)
{
    if(low<high)
    {
        int mid=(low+high)/2;
        MergeSort(A,low,mid);//排序好前一半
        MergeSort(A,mid+1,high);//排序好后一半
        Merge(A,low,mid,high);//将两个排序好的数组合并
    }
}

void print(int *a)
{
    for(int i=0;i<N;i++)
    {
        printf("%3d",a[i]);
    }
    printf("\n");
}

//归并排序
int main() {
    int A[7]={49,38,65,97,76,13,27};
    MergeSort(A,0,6);
    print(A);
    return 0;
}

3、时间复杂度与空间复杂度

        MergeSort 函数的递归次数是log2n,Merge 函数的循环了n次，因此时间复杂度是 O(nlog2n).归并排序最好、最坏、平均时间复杂度都是 O(nlog2n).归并排序的空间复杂度是 O(n)，因为使用了数组B，它的大小与A一样，占用n个元素的空间。

稳定性是指排序前后，相等的元素位置是否会被交换；

复杂性是指代码编写的难度 。

———————————————————————————————————————————

目录

一、C语言督学营（课上代码） 

二、C语言督学营（课上笔记）

三、C语言督学营（课后习题OJ题解）