机器学习一 解析解方法求解线性回归

一.MSE损失函数公式

1.已知我们损失函数MSE的公式如下:

MSE损失函数，从公式我们也可以看出来MSE名字的来历，mean squared error ，上式也叫做最小二乘。

二.推导出θ的解析解公式

1. 明确目标:θ为何值使得损失函数最小,且损失函数是凸函数。利用上述公式开始推导:
   
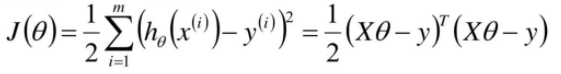
   2.推导函数的一阶导(或求梯度),此阶段我们的已知是X和y，未知是θ，所以和θ无关的部分求导忽略不记.

补充相关知识点

3.开始求一阶导


4.假设我们找到了最优解,即梯度为0。则令该函数等于0,进而求得我们θ对应的解析解公式:

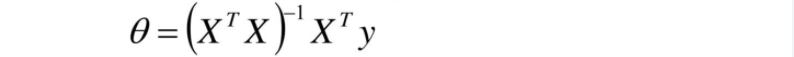
三.求解线性回归方程

1.求解线性回归算法模型

import numpy as np
import matplotlib.pyplot as plt

# 构建X和y数据
X = 2 * np.random.rand(100,1) 
# 因为 randn函数是标准的正太分布,误差符合均值为0
y = 5 + 4 * X + np.random.randn(100,1)  #w0=5 w1=4 np.random.randn(100,1)为误差
X_w0 = np.ones(100,1)  #w0截距项,
X_b = np.c_[X_w0, X] #给X添加全为1的X0

#相关知识点
#求逆: np.linalg.inv()
#点乘: np.dot()
# 根据θ解析解公式可得
theta = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)
print(theta) # 已求得θ

#做模型预测 一元线性公式 y_hat = w * X
# 构建预测数据集
x_new = np.array([[0],
                  [2]])
x_new_b = np.c_[np.ones((2,1)),x_new] #x0
y_predit= x_new_b.dot(theta) # 预测结果

# 画图
plt.plot(x_new,y_predit,'r-') # 画出这条线
plt.plot(X,y,'b.') # 画出这些点
plt.axis(0,2,0,15) # axis取值
plt.show()

运行结果:

2.求解多元线性回归类算法模型(多元为例)

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

# 构建X和y数据
X1 = 2 * np.random.rand(100,1) 
X2 = 2 * np.random.rand(100,1)
X = np.c_[X1,X2]
y = 4 + 3 * X1 + 5 * X2 + np.random.randn(100,1)  #w0=4 w1=3 w2=5 np.random.randn(100,1)为误差
# 因为 randn函数是标准的正太分布,误差符合均值为0

lin_reg = LinearRegression() #fit_intercept=True 系数为w0的截距项,本质就是X身上加上X0,然后解方程
lin_reg.fit(X,y)
print(lin_reg.intercept_,lin_reg.coef_) # 截距项和参数系数

#构建预测数据集 模型预测
X_new =np.array([[0,0],   
                 [2,1],
                 [2,4]])
print(lin_reg.predict(X_new))