堆和堆排序详解

手写堆与堆排序

Heap堆

堆是一棵完全二叉树，因此我们可以用数组来存储堆，而不是用链表存储。

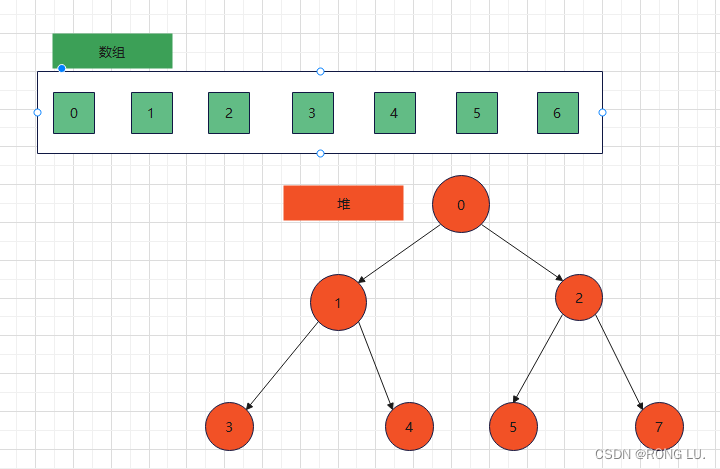
从数组的下标0开始存储元素，nums[0]存储的是这棵二叉树的root节点，nums[1]存储root节点的左子树节点，nums[2]存储root节点的右子树节点。

那么针对元素 nums[x],它的左子树是nums[2x+1],右子树是nums[2x+2]。

class Heap{
    private int size=0;
    private int max_size;
    private int[] nums;
    public Heap(int max_size){
        this.max_size=max_size;
        this.nums=new int[max_size+1];
    }

    public Heap(){
        this(10000);
    }
    public int size(){
        return this.size;
    }
}

按照堆的不同定义，我们可以把堆分为大根堆和小根堆。

大根堆：由每个元素的值都大于等于其子元素的值的元素组成的堆叫做大根堆，其中root为堆的最大值。

小根堆：由每个元素的值都小于等于其子元素的值的元素组成的堆叫做小根堆，其中root为堆的最小值。

大根堆和小根堆的实现方式基本相同，本文这里实现小根堆。读懂文章，你可以很轻松实现大根堆。

小根堆需要支持下列几种基本操作

1. 返回当前堆中的最小值 public int min()
2. 弹出当前堆中的最小值 public int pop()
3. 向堆中插入一个新元素 public void push(int e)

min()方法

min()方法的实现最简单，因为我们nums[0]存的是堆顶的元素，按照小根堆的定义来说，堆顶元素是堆的最小值，只需要返回nums[0]。

    public int min(){
        if(size==0)throw new RuntimeException("堆中没有元素!");
        return nums[0];
    }

为了实现pop()和push()我们定义两个新的操作

down():修改一个元素的值后，当前的二叉树可能不满足堆的定义，如果这个元素太大了，要交换该元素和其子元素的位置。

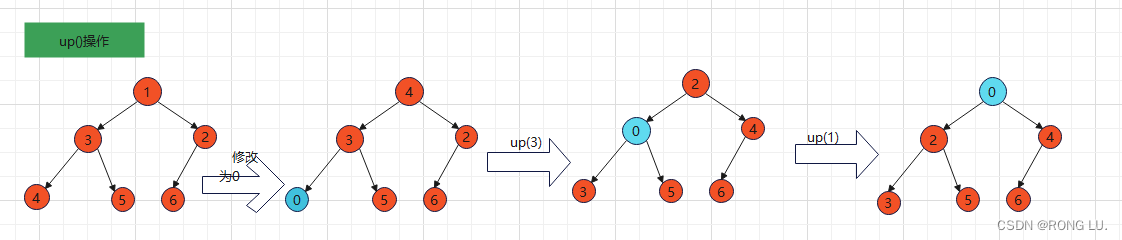
up():修改一个元素的值后，当前二叉树可能不满足堆的定义，如果这个元素太小了，要交换该元素和其父元素的位置。

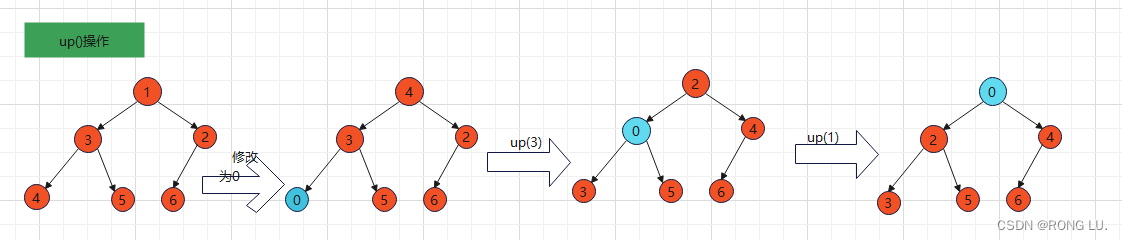
有了这两个操作后，我们便可以简单的实现pop()和push()方法，

push()方法

我们将需要插入的元素放入数组的末尾，这个元素已经在堆的最底层了，因此它的实际的存储位置要么不变，要么在上层。我们对这个元素执行up()操作，即可使数组满足堆的性质

    public void push(int e){
        nums[size]=e;
        up(size++);
    }

pop()方法

pop()会删除最小值，我们知道最小值是nums[0],可以把nums[0]的值修改为nums[size-1],在删除最后一个元素，然后执行down(0)方法。

    public int pop(){
        if(size==0)throw new RuntimeException("堆中没有元素!");
        int del=nums[0];
        nums[0]=nums[size-1];
        size--;
        down(0);
        return del;
    }

down（）方法和up（）方法

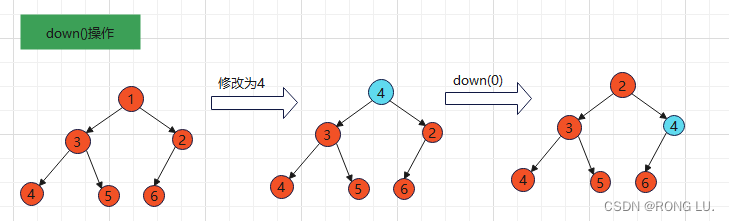
//down()和up()都是我们类内部的操作，供pop和push调用。因此用private修饰，不提供给外部调用。
private void down(int index){
    //先让n默认为index
    int n=index;
    //index*2+1是左子树，这个分支的含义是：如果这个元素存在左子树，并且左子树的值小于n的值，使n变成左子树
    if(index*2+1<size && nums[index*2+1]<nums[n]){
        n=index*2+1;
    }
     //index*2+2是右子树，这个分支的含义是：如果这个元素存在右子树，并且右子树的值小于n的值，使n变成右子树
    if(index*2+1<size && nums[index*2+1]<nums[n]){
        n=index*2+1;
    }
    //如果n没有改变，说明元素index不存在左右子树，或者存在左右子树，但子树的值都大于元素index的值。因此当前情况满足堆的定义直接返回
   	if(n==index)return ;
    //交换index和n
    nums[index]^=nums[n];
    nums[n]^=nums[index];
    nums[index]^=nums[n];
    //交换后有可能仍不满足堆的定义，因此递归调用
    down(n);
    
}

down（）的时间复杂度分析：

假设堆的元素个数是n，那么这棵完全二叉树的高度是logn，down()最多调用logn次，因此down()的时间复杂度在O(logn)

//同样用private修饰，提供良好的封装性。
private void up(int index){
	//在根节点了，不能继续up了
    if(index==0)return ;
    //(index-1)/2表示父节点
    if(nums[(index-1)/2]>nums[index]){
        //交换父子节点的值
        nums[(index-1)/2]^=nums[index];
    	nums[index]^=nums[(index-1)/2];
    	nums[(index-1)/2]^=nums[index];
        //同样对交换后的节点进行递归
        up((index-1)/2);
    } 
}

up（）的时间复杂度分析：

假设堆的元素个数是n，那么这棵完全二叉树的高度是logn，up()同样最多调用logn次，因此up()的时间复杂度也是O(logn)

构建堆的时间复杂度分析

将一个长度为n的数组构建成堆，分析时间复杂度。

自顶向下

从第一个节点开始，执行up()操作，直到全部元素都进堆中,共执行n次push()。

故时间复杂度O(nlogn)

自底向下

假设二叉树共有n个节点，那么共有logn层，最后一层有n/2个元素，倒数第二层有n/4个元素，倒数第三层有n/8个元素，以此类推

最后一层的元素不必执行down()，因为已经在最底层。因此从第n/2个元素开始执行down操作

for(int i=size/2;i>=0;i--){
    down(i);
}

在这里简单的用循环次数乘以down()操作的时间复杂度，会得到总体的执行次数是(n/2)*logn,时间复杂度同样在O(nlogn)。

但仔细分析，down()操作的时间复杂度和元素所在的二叉树深度有着关系

如果说是倒数第二层的元素，他们最多down到倒数第一层，因此down()的时间复杂度是O(1)。同理倒数第三层的元素执行down()操作时间复杂度是O(2)。倒数第n层执行down()操作的时间复杂度是O(n-1)。

结合着上面说的倒数第二层有n/4个元素，倒数第三层有n/8个元素，倒数第n层有n/(2^n)个元素。

那么总的时间复杂度:
$$\begin{gathered} (n/4)\ast 1+(n/8)\ast 2+(n/16)\ast 3...+(n/2^n)\ast (n-1) \\ =n(1\ast (1/4)+2\ast (1/8)+3\ast (1/16)...) \\ =n\sum _1^{n-1}n\ast (1/2{)}^{n+1} \\ 错位相减可得：\sum _1^{n-1}n\ast (1/2{)}^{n+1}=1-2^{-n}-n\ast 2^{-n-1} \\ 求极限可得：li{m}_{n\to \infty }\sum _1^{n-1}n\ast (1/2{)}^{n+1}=1 \\ 当n取值较大时候n\sum _1^{n-1}n\ast (1/2{)}^{n+1}=n\ast 1=n \\ 故时间复杂度为O(n) \end{gathered}$$

堆排序

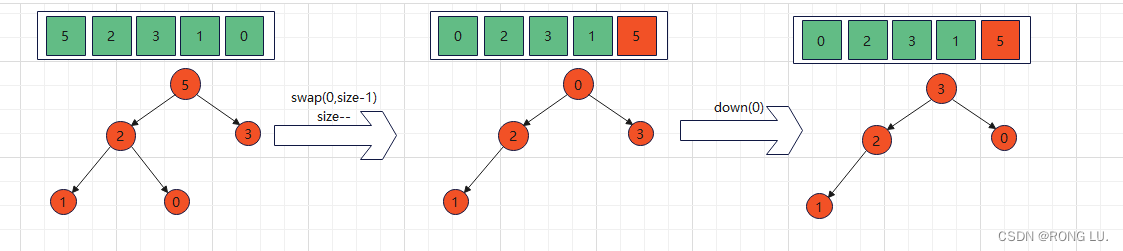
首先将一个数组构建成一个大根堆，堆顶的元素是数组的最大值，交换堆顶元素的值和末尾元素的值，然后删除末尾元素，对堆顶元素进行down()操作。这样便将最大的元素放到的对应的位置，同时也让剩下的n-1个元素继续保持大根堆的性质。

那么对上述操作执行n次便可得到一个排好序的数组，并且此时我们维护的大根堆大小为0。

代码

class HeapSort {
    int size=0;
    int[] nums;
    public int[] heapSort(int[] nums) {
        this.size=nums.length;
        this.nums=nums;
        //建堆
        for(int i=(nums.length)/2;i>=0;i--){
            down(i);
        }
        for(int i=0;i<nums.length-1;i++){
            //交换堆顶元素和末尾元素
            int temp=nums[0];
            nums[0]=nums[size-1];
            nums[size-1]=temp;
            //删除末尾元素
            size--;
            down(0);  
        }
        
        
        return nums;
    }
    private void down(int idx){
        int n=idx;
        if(2*idx+1<size && nums[n]<nums[2*idx+1])n=2*idx+1;
        if(2*idx+2<size && nums[n]<nums[2*idx+2])n=2*idx+2;
        if(n!=idx){
            int temp=nums[idx];
            nums[idx]=nums[n];
            nums[n]=temp;
            down(n);
        }
    }
}

时间复杂度分析

建堆消耗O(n)的时间加上n次down()。故时间复杂度是O(nlogn);

最后

第一次尝试自己写一篇比较详细的算法笔记，虽然画图和在markdown上打数学公式花费了好多时间，但也加深了自己对堆这个数据结构的理解。嘿嘿，洋洋洒洒几千个字写下来成就感满满，继续努力！奥里给！