理解使用递归及堆栈的算法处理八皇后问题

八皇后算法，是大多数计算机编程教程讲解到递归部分，几乎必讲的一个经典算法题，甚至在许多程序员职位面试中，都出现了这道题目。知乎上有个主题就是用10行代码，解决八皇后问题。本人刚刚转行软件，目前研读到递归这一块内容。现在把自己的粗浅理解写下来。
首先是基础知识：

• C语言，这个我想只要工科类的学生，肯定学过，有基本数据结构，三种控制流，输入，输出知识足够。现在有些人，使用C++的环境来写不包含对象的C程序，这会简化C语言在输入输出方面的繁琐学习，值得推荐。而C++的特点是，在C语言的基础上加入面向对象的支持，也就是“类”，说白了就是把原来的结构体里面加入与这些数据结构相关的函数。而把面向对象拆分开，不写成“类”，在某些情况下，可以更好地理解程序的结构。本文在网友分享的八皇后程序基础上，修改为比较好理解的结构化程序。
• 函数。这个主要是理解函数调用的原理，重点是每次调用函数，都会开辟一片新的内存空间，函数参数都会被复制一次。
• 递归。递归的调用可以用函数调用来理解，必须有一个“结束”条件，否则容易造成程序死循环。
• 栈。主要是“后入先出”的思想。如何用数组或者链表来创建栈

有了基础知识就能来看看八皇后算法了。
首先是声明一个二维数组，保存棋盘信息，

#define StackSize 8 /*最多放8个皇后*/
int queen[StackSize][StackSize]={0}; /*棋盘*/

然后声明一个大小为8的一维数组，存储皇后的行（列）位置，这里是一个栈，top为栈顶指针。

int top=-1;                          /*栈顶指针*/ 
int data[StackSize];                  /*存储皇后位置*/ 

摆放皇后函数如下：

/*放N皇后的递归函数*/
void Place(int row)//摆放皇后
{
    bool Judgement();//位置是否合法
    void SeqStack();//关键点1：每一次摆放都会初始化空栈，即栈顶指针=-1
    void Output();//输出结果
    for (int col=0;col<StackSize;col++)//结束条件为col=8
    {
        Push(col);//将合法位置入栈
        if (Judgement()) //判断位置合法
        {
            if (row<StackSize-1) //若还没有放到第八个皇后，则递归进行下一个皇后的放置
                PlaceQueen(row+1);                                    
            else
            {             //摆放完8个皇后，输出结果
                ans++;  //解数加1
                Output(); //打印成功的棋盘
            }
        }
        Pop();//若不符合条件则出栈                                                                    
    }
}

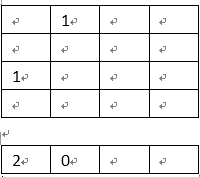
以4皇后为例，分析main函数调用place摆放函数过程。place(0)，也就是在第0行放一个皇后，data栈将“0”入栈。此时棋盘信息和栈内容如下：

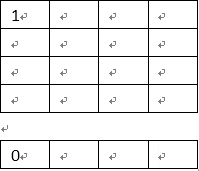
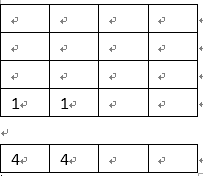
这个位置是合法的，所以继续调用place(1)，也就是在第1行放一个皇后，data栈将“0”入栈,判断发现(1,0)这个位置不合法（在皇后同一行），于是将“0”出栈。以此类推，(1,1)也不合法，(1,2)合法，将2入栈，继续调用place(2).经判断第2行没有合法的摆放位置。程序返回到place(1)，并且出栈。返回到place(0)，出栈。那此时col的值加1变为了1，也就是这次就要在(0,1)这个位置放第一个皇后.给出调用place(1)~place(3)之后的棋盘信息和栈空间

皇后已经摆了4个，就可以调用output函数，打印棋盘信息同时解变量值加1.出栈程序回到place(0)，col加1变为2，继续判断。以此类推。

还有一个难点，是判断位置合法性的函数。八皇后游戏规定，皇后可以吃掉“同行、同列、对角线、斜对角线”上的棋子，那么8个皇后必然是不同行不同列的，这个可以用下面代码判断

data[top]==data[i]

就是说，假设现在place(0)将(0,4)入栈，递归调用place(1)，如果将(1,4)入栈，那就是同一行同一列，必须舍弃，这里data[top]=4，就是刚入栈的(1,4)信息，data[0]=4就是原来栈中所存的皇后位置信息(0,4)，二者相等，位置不合法。

而对角线的判断，可以用下面代码

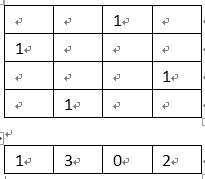
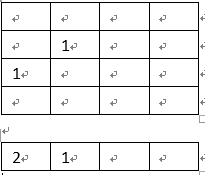
abs(data[top]-data[i]))==(top-i)

top-i的值就是皇后之间的非法相对距离，值为0、1、2….，也就是同一条对角线或者斜对角线。data[top]-data[i]为2个皇后的实际的相对距离。比如假设现在place(0)将(0,3)入栈，递归调用place(1)，如果将(1,2)入栈，那就是在右上角的对角线上，必须舍弃，这里data[top]=2，就是刚入栈的(1,2)信息，data[0]=3就是原来栈中所存的皇后位置信息(0,3)，二者之差=1，就是相对距离为1，位置不合法。

如果上面递归调用place(1)，将(1,0)入栈，那么相对距离变为2-0=2，不是相差一层（top-i=1），那就合法

---

附上完整八皇后C++代码

#include <iostream>
#include<cmath>
using namespace std;
#define StackSize 8 /*最多放8个皇后*/
int queen[StackSize][StackSize]={0}; /*棋盘*/
int ans=0;                           /*解数*/
int top=-1;                          /*栈顶指针*/ 
int data[StackSize];                  /*存储皇后位置*/ 

/*入栈*/ 
void Push(int x)                                          //入栈操作
{
    top++;                                                           //栈顶指针上移
    data[top]=x;
}
/*出栈*/ 
void Pop()                                              //出栈操作
{
    top--;                                                           //栈顶指针下移
}

void SeqStack(){top=-1;}                                              //构造函数，初始化空栈

/*放N皇后的递归函数*/
void PlaceQueen(int row)                                //在栈顶放置符合条件的值的操作,即摆放皇后
{
    bool Judgement();
    void SeqStack();                                    //关键点1：每一次摆放都会初始化空栈
    void Output();
    for (int col=0;col<StackSize;col++)                              //穷尽0~7，即穷尽列
    {
        Push(col);
        if (Judgement())                                             //判断摆放皇后的位置是否安全
        {
            if (row<StackSize-1)                                     //若还没有放到第八个皇后，则进行下一个皇后的放置
                PlaceQueen(row+1);                                    
            else
            {
                ans++;                                               //解数加1
                Output();                                            //打印成功的棋盘
            }
        }
        Pop();                                                       //若不符合条件则出栈        
    }
}

/*关键点2：判断合法性*/
bool Judgement()
{
    for(int i=0;i<top;i++)                                           //依次检查前面各行的皇后位置
        if(data[top]==data[i]||(abs(data[top]-data[i]))==(top-i))    //判断是否在同一列同一斜线
            return false;                                            /*第一个条件，使每次入栈的数字不同层（行）*/   
    return true;                                                     /*top-i的值就是皇后之间的非法相对距离，值为0、1、2....，也就是同一条对角线或者斜对角线。data[top]-data[i]为2个皇后的实际的相对距离。*/  
}

/*输出棋盘*/ 
void Output()                                          //将栈的数组形式打印成棋盘形式
{
    cout<<"NO."<<ans<<":"<<endl;                                    
    for(int i=0;i<StackSize;i++)
    {
        for(int j=0;j<data[i];j++)
            cout<<"- ";                                             //不放置处打印“-”
        cout<<"Q";                                                  //放置处打印“Q”
        for(int j=StackSize-1;j>data[i];j--)
            cout<<" -";
        cout<<endl;                                                 //换行
    }
    cout<<endl;
}
int main()
{
    PlaceQueen(0);                                        //从栈底开始赋值
    cout<<"the total number of solutions is:"<<ans<<endl;       //输出摆放方法的总数
    system("pause");
    return 0;
}