相关分析的简要介绍

相关分析

1 相关关系

相关关系指变量之间存在着非确定性依存关系。即当一个或一组变量每取一个值时，相应的另一个变量可能有多个不同值与之对应。

相关关系可以理解为多个变量均值之间的一种数量关系！

1.1 相关关系的种类

按变量的个数分类：

• 研究2个变量之间的关系，为单相关；
• 研究1个变量与N个变量之间的关系，为复相关；
• 就多个变量测定其中两个变量的相关程度而假定其他变量不变，为偏相关。

1.2 相关分析的特点

1. 两个变量全是随机变量，X是随机变量，Y也是随机变量；
2. 变量X与变量Y只能计算出一个相关系数，相关系数是唯一的；
3. 计算相关系数时，变量X与Y获取的资料方式相同。

2 相关性度量

2.1 相关系数

对变量之间关系密切程度的度量

若相关系数是根据总体全部数据计算的，称为总体相关系数，记为 $\rho$。若是根据样本数据计算的，则称为样本相关系数， 记为 r。

根据数值大小来判定相关密切程度方面，尚无一致意见。一般常划分为四级：$|r|$ 数值在0.3以下者视为不相关，0.3~0.5属低度相关，0.5-0.8属显著相关，0.8以上属高度相关（仅供参考，需根据实际情况判断）。

为了定量的描述线性相关性，统计学奠基人K. Pearson提出了Pearson积差相关系数、心理学家CE. Spearman提出了Spearman等级相关系数、统计学家M. Kendall提出了Kendall秩相关系数。这三种相关系数最具有代表性、应用也最广泛，它们既有联系又有不同，分别有不同的适用场景。

重要参考： 作者：Treant；出处：http://www.cnblogs.com/en-heng/

2.1.1 Pearson相关系数

Pearson相关系数 (Pearson correlation coefficient)用于度量两个变量X、Y的相关性，定义如下：
$$r=\frac{{\sigma }_{XY}}{{\sigma }_X{\sigma }_Y}=\frac{{\sum }_{i=1}^n(X_i-\overline{X})(Y_i-\overline{Y})/N}{\sqrt{{\sum }_i^n(X_i-\overline{X}{)}^2/N}\sqrt{{\sum }_i^n(Y_i-\overline{Y}{)}^2/N}}=\frac{{\sum }_{i=1}^n(X_i-\overline{X})(Y_i-\overline{Y})}{\sqrt{{\sum }_i^n(X_i-\overline{X}{)}^2}\sqrt{{\sum }_i^n(Y_i-\overline{Y}{)}^2}}$$
上述公式又被称为相关系数的积差法计算公式，其中分子位置的 ${\sigma }_{XY}$ 表示变量X与Y的协方差(消除了变量个数的影响)，分母位置的两变量的标准差 ${\sigma }_X,{\sigma }_Y$ 的作用是使不同变量的协方差标准化，用于消除变量本身数值大小的影响。

注意：

• 此公式计算的是变量之间的线性相关系数。如果变量之间属于非线性相关，则此公式失效；
• 相关系数计算出的结果是唯一的，并且数值在 $\pm 1$ 之间；
• 样本资料说明总体时，要进行假设检验；
• 其分析的是直接关系，不是间接关系；

下图给出了当Pearson相关系数为不同值时X和Y的散点图（以下三张图片均来自于Wikipedia）：

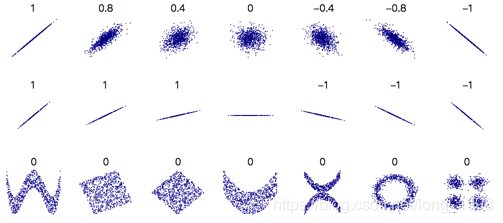
2.1.2 Spearman相关系数

Spearman相关系数实际上就是将变量X和Y替换成其对应等级x, y的Pearson相关系数：
$$\rho =\frac{{\sum }_{i=1}(x_i-\overline{x})(y_i-\overline{y})}{\sqrt{{\sum }_i(x_i-\overline{x}{)}^2}\sqrt{{\sum }_i(y_i-\overline{y}{)}^2}}$$
相较于Pearson相关系数，Spearman相关系数更能描述两个变量之间的单调性的相关性，对于样本中的显著离群点更为不敏感。比如，下图中变量X和Y的Pearson相关系数、Spear-man相关系数分别为0.88与1，显然Spearman相关系数更好地刻画了两个变量增长趋势的相关性。

下图更好地表现出了Spearman相关系数的抗噪音性：

2.1.3 Kendall相关系数

Kendall相关系数是另一种等级相关统计量，其主要思想是根据两个变量序对的一致性 (concordance)来判断相关性的。一致性序对 (concordant pair)定义如下：如果变量对$(X_i,Y_i)$、$(X_j,Y_j)$ 且$ i \neq j$ 满足当$X_i<X_j$ 时 $Y_i<Y_j$，或者当$X_i>X_j$时$Y_i>Y_j$。反之，则为非一致性序对。

Kendall相关系数的定义如下：
$$\tau =\frac{P-Q}{n(n-1)/2}$$其中，P为一致性序对的个数，Q为非一致性序对个数，则P+Q=n(n−1/2)，因此上式可改写为：$\tau =\frac{4P}{n(n-1)/2}-1$， 显然τ的取值范围为[-1, 1] 。

2.2 线性相关的假设检验

基本步骤：

1. 提出原假设与备择假设 $H_0:\rho =0，H_1:\rho \ne 0$
2. 给定显著性水平 $\alpha$
3. 选择检验方法，构建检验统计量
4. 将检验统计量与临界值比较，如检验统计量的绝对值大于临界值，则拒绝原假设，否则，就不拒绝原假设。

检验方法：
t 检验法：
$$t=\frac{r}{\sqrt{\frac{1-r^2}{n-2}}}$$r 检验法：用已经算好的 r 作为检验统计量，其临界值可以在附表中找到。