编辑距离问题:
编辑距离,又称Levenshtein距离,是指两个字串之间,由一个转成另一个所需的最少编辑操作次数。许可的编辑操作包括将一个字符替换成另一个字符,插入一个字符,删除一个字符。
例如将kitten一字转成sitting:
- sitten (k→s)
- sittin (e→i)
- sitting (→g)
俄罗斯科学家Vladimir Levenshtein在1965年提出这个概念。
【以上转自Weki百科】《算法导论》(p218)上对这个问题的描述更为详细。此处对概念不做过多说明,这是一个典型的动态规划问题,用一句话来描述最优解就是求将源字符串src转换为目的字符串tar,所需要进行的最小操作数。
为此递归表达式如下:
dp[i][j]表示由字串s1[1..i]转换为字串s2[1,,j]的最小操作数,显然:
dp[0][j]=j*cost(delete);
dp[i][0]=i*cost(insert);
dp[i][j]=min{ dp[i-1][j-1]+cost(copy) if src[i]=tar[j] or dp[i-1][j-1]+cost(replace) if src[i]!=tar[j]
or dp[i-1][j]+cost(delete),
or dp[i][j-1]+cost(insert)}
代码如下:
#include <iostream>
#include <vector>
#include <string>
using namespace std;
const int costCopy=0;
const int costReplace=1;
const int costDelete=1;
const int costInsert=1;
int levenshteinDistance(const string &s1,const string &s2){
int len1=s1.size();
int len2=s2.size();
if(!len1) return len2;
if(!len2) return len1;
vector <vector <int> > dp(len1+1,vector <int>(len2+1,0));
//initialize dp
for(int i=1;i<len1+1;i++){
dp[i][0]=dp[i-1][0]+costDelete;
}
for(int j=1;j<len2+1;j++){
dp[0][j]=dp[0][j-1]+costInsert;
}
//dp
for(int i=1;i<=len1;i++){
for(int j=1;j<=len2;j++){
int minDis=0;
if(s1[i-1]==s2[j-1]){
minDis=dp[i-1][j-1]+costCopy;
}
else{
minDis=dp[i-1][j-1]+costReplace;
}
int tempDis=dp[i-1][j]+costDelete;
if(minDis>tempDis){
minDis=tempDis;
}
tempDis=dp[i][j-1]+costInsert;
if(minDis>tempDis){
minDis=tempDis;
}
dp[i][j]=minDis;
}
}
cout<<"***************************"<<endl;
for(int i=0;i<=len1;i++){
for(int j=0;j<=len2;j++){
cout<<dp[i][j]<<" ";
}
cout<<endl;
}
cout<<"**************************"<<endl;
return dp[len1][len2];
}
int main(){
string s1("sailn");
string s2("failing");
cout<<"编辑距离:"<<levenshteinDistance(s1,s2);
return 0;
}需要说明的一点是,我在程序中将copy,replace,insert以及delete操作的代价都设为特定的常数,并采用常量形式表示,程序运行结果如下:








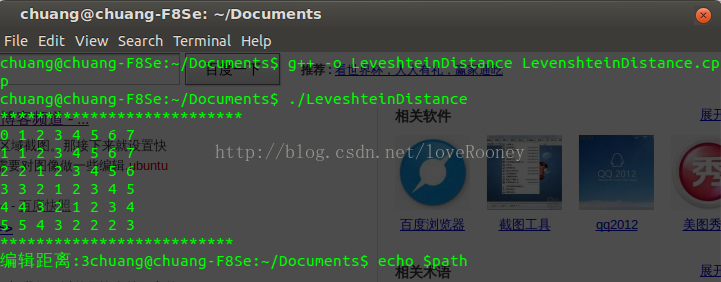
















 683
683

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








