第一章 空间解析几何与向量代数（1）

第一节 空间直角坐标系

数学史话

        17世纪中叶，费马（Fermat）和笛卡尔（Descartes）把二维平面解析几何，推广到三维空间。他们指出，三维空间的几何图形，可用三维空间动点的轨迹来表达，也可以用代数方程来表达；而空间中的一个动点，则是三元不定方程的一组解（𝒙, 𝒚, 𝙯），并且这个不定方程的所有解，构成了三维空间中的曲面。

        费马（Fermat）简单讲述了他的三维解析几何的思想，他认为各种曲面，如抛物面、双曲面等，都是在三维空间的。因此，三维空间曲面上的曲线，一定也是三维的，它们可以用三个未知量的方程表出。

        笛卡尔（Descartes）在他的《方法论》（1637年）附录之一的《几何》中指出，一个三元不定方程的一组解是三维空间中轨迹上的一个点，所有解的轨迹是一个曲面。

        18世纪，数学家在继续研究二维平面解析几何的同时，开始了对三维空间解析几何的系统研究。研究的结果，使得一门新的几何学诞生，这就是后来的“微分几何”。

        18世纪，法国数学家克莱罗（Clairaut），他在几何上把空间曲线看成是两个曲面的交线，在代数中他把三维曲面方程表达为含有𝒙, 𝒚, 𝙯三个未知量的方程。

        克莱罗（Clairaut）的论述，用现代的写法就是，一个不定代数方程𝒇(𝒙, 𝒚, 𝙯)=0所有的解的轨迹，在几何上是三维空间的曲面。如果两个曲面相交，那么在代数上的表达是，代数方程𝒇(𝒙, 𝒚, 𝙯)=0和𝒈(𝒙, 𝒚, 𝙯)=0有公共的解，而这些所有的解的轨迹组成的曲线，就是两个曲面的交线，这条交线就是三维空间的曲线。

        1731年，克莱罗（Clairaut）在他的数学著作《关于双重曲率曲线的研究》中，他把空间曲线称为“双曲率线”，这是因为他注意到，空间曲线在两个互相垂直平面上的投影，各有一个曲率，而这二个曲率属于同一条空间曲线，所以克莱罗（Clairaut）把空间曲线称为“双曲率线”。

        

一、空间直角坐标系

约定Z轴的正方向符合右手规则：用右手握住Z轴，四指从X轴正向以90度转向Y轴正向时，大拇指的方向即为Z轴正向。按此约定的坐标系又称右手系。

1、空间直角坐标系的相关概念

• 在空间直角坐标系Oxyz中，任意两个坐标轴可确定一平面，称为坐标面。由x轴和y轴确定的坐标面称为xOy面，类似有yOz面和zOx面。
• 三个坐标面把空间分为八个部分，每一部分称为一个卦限，从第一个卦限开始按逆时针方向分别用罗马数字命名。

如何根据点坐标判别处于哪一个卦限，一般步骤可分2步：

• 首先根据z坐标值（竖坐标）区分上下界面（z > 0属一、二、三、四限；z < 0属五、六、七、八限）。
• 然后根据x，y坐标值（可画出平面直角坐标系图）来判别具体处于哪一个卦限。

点与坐标：

向量与空间中的点M以及一组有序数x, y, z之间存在一一对应的关系，称有序数x, y, z为向量以及点M的坐标，记作= (x, y, z) 和 M(x, y, z)。

特殊点的坐标：

原点O(0, 0, 0) 

坐标轴上的点P，Q，R，至少有两个0坐标值

坐标面上的点A，B，C，至少有一个0坐标值

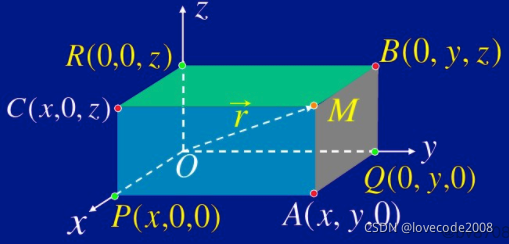
空间中两点的距离公式

空间两点之间距离公式的推导过程是两次勾股定理的运用。

2、向量的坐标表示

在建立了空间直角坐标系后，对于任一空间向量 ， 我们都可以通过平移使该向量的起点位于坐标原点O处，此时向量的终点记为M，按这种方式，每一空间向量都有空间中一点唯一与之对应。

空间直角坐标系中的点关于什么轴/平面对称，什么坐标就不变，其余的分坐标均取反。