1. LATEX
1.1 常用字母



1.2 常用数组

1.3 LaTex常用的数学字体
正常字体:\mathnormal{} --> normal
-
大写: A , B , C , D , E , F , Z , H , I , J , K , L , M , N , O , P , Q , R , S , T , U , V , W , X , Y , Z \mathnormal{A,B,C,D,E,F,Z,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z} A,B,C,D,E,F,Z,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z
-
小写: a , b , c , d , e , f , g , h , i , j , k , l , l , n , o , p , q , r , s , t , u , v , w , x , y , z \mathnormal{a,b,c,d,e,f,g,h,i,j,k,l,l,n,o,p,q,r,s,t,u,v,w,x,y,z} a,b,c,d,e,f,g,h,i,j,k,l,l,n,o,p,q,r,s,t,u,v,w,x,y,z
罗马体:\mathrm{} --> roman
-
大写: A , B , C , D , E , F , Z , H , I , J , K , L , M , N , O , P , Q , R , S , T , U , V , W , X , Y , Z \mathrm{A,B,C,D,E,F,Z,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z} A,B,C,D,E,F,Z,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z
-
小写: a , b , c , d , e , f , g , h , i , j , k , l , l , n , o , p , q , r , s , t , u , v , w , x , y , z \mathrm{a,b,c,d,e,f,g,h,i,j,k,l,l,n,o,p,q,r,s,t,u,v,w,x,y,z} a,b,c,d,e,f,g,h,i,j,k,l,l,n,o,p,q,r,s,t,u,v,w,x,y,z
斜体:\mathit{} --> italic
-
大写: A , B , C , D , E , F , Z , H , I , J , K , L , M , N , O , P , Q , R , S , T , U , V , W , X , Y , Z \mathit{A,B,C,D,E,F,Z,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z} A,B,C,D,E,F,Z,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z
-
小写: a , b , c , d , e , f , g , h , i , j , k , l , l , n , o , p , q , r , s , t , u , v , w , x , y , z \mathit{a,b,c,d,e,f,g,h,i,j,k,l,l,n,o,p,q,r,s,t,u,v,w,x,y,z} a,b,c,d,e,f,g,h,i,j,k,l,l,n,o,p,q,r,s,t,u,v,w,x,y,z
黑粗体:\mathbf{} --> boldface
-
大写: A , B , C , D , E , F , Z , H , I , J , K , L , M , N , O , P , Q , R , S , T , U , V , W , X , Y , Z \mathbf{A,B,C,D,E,F,Z,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z} A,B,C,D,E,F,Z,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z
-
小写: a , b , c , d , e , f , g , h , i , j , k , l , l , n , o , p , q , r , s , t , u , v , w , x , y , z \mathbf{a,b,c,d,e,f,g,h,i,j,k,l,l,n,o,p,q,r,s,t,u,v,w,x,y,z} a,b,c,d,e,f,g,h,i,j,k,l,l,n,o,p,q,r,s,t,u,v,w,x,y,z
黑板体(空心体):\mathbb{} --> blackboard
-
大写: A , B , C , D , E , F , Z , H , I , J , K , L , M , N , O , P , Q , R , S , T , U , V , W , X , Y , Z \mathbb{A,B,C,D,E,F,Z,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z} A,B,C,D,E,F,Z,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z
-
小写: a , b , c , d , e , f , g , h , i , j , k , l , l , n , o , p , q , r , s , t , u , v , w , x , y , z \mathbb{a,b,c,d,e,f,g,h,i,j,k,l,l,n,o,p,q,r,s,t,u,v,w,x,y,z} a,b,c,d,e,f,g,h,i,j,k,l,l,n,o,p,q,r,s,t,u,v,w,x,y,z
书法艺术体:\mathcal{} --> calligraphy
-
大写: A , B , C , D , E , F , Z , H , I , J , K , L , M , N , O , P , Q , R , S , T , U , V , W , X , Y , Z \mathcal{A,B,C,D,E,F,Z,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z} A,B,C,D,E,F,Z,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z
-
小写: a , b , c , d , e , f , g , h , i , j , k , l , l , n , o , p , q , r , s , t , u , v , w , x , y , z \mathcal{a,b,c,d,e,f,g,h,i,j,k,l,l,n,o,p,q,r,s,t,u,v,w,x,y,z} a,b,c,d,e,f,g,h,i,j,k,l,l,n,o,p,q,r,s,t,u,v,w,x,y,z
书写体:\mathscr{} --> script
-
大写: A , B , C , D , E , F , Z , H , I , J , K , L , M , N , O , P , Q , R , S , T , U , V , W , X , Y , Z \mathscr{A,B,C,D,E,F,Z,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z} A,B,C,D,E,F,Z,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z
-
小写: a , b , c , d , e , f , g , h , i , j , k , l , l , n , o , p , q , r , s , t , u , v , w , x , y , z \mathscr{a,b,c,d,e,f,g,h,i,j,k,l,l,n,o,p,q,r,s,t,u,v,w,x,y,z} a,b,c,d,e,f,g,h,i,j,k,l,l,n,o,p,q,r,s,t,u,v,w,x,y,z
德文尖角体(哥特体):\mathfrak{} --> fraktur (aka gothic)
-
大写: A , B , C , D , E , F , Z , H , I , J , K , L , M , N , O , P , Q , R , S , T , U , V , W , X , Y , Z \mathfrak{A,B,C,D,E,F,Z,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z} A,B,C,D,E,F,Z,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z
-
小写: a , b , c , d , e , f , g , h , i , j , k , l , l , n , o , p , q , r , s , t , u , v , w , x , y , z \mathfrak{a,b,c,d,e,f,g,h,i,j,k,l,l,n,o,p,q,r,s,t,u,v,w,x,y,z} a,b,c,d,e,f,g,h,i,j,k,l,l,n,o,p,q,r,s,t,u,v,w,x,y,z
无衬线体:\mathsf{} --> sans serif
-
大写: A , B , C , D , E , F , Z , H , I , J , K , L , M , N , O , P , Q , R , S , T , U , V , W , X , Y , Z \mathsf{A,B,C,D,E,F,Z,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z} A,B,C,D,E,F,Z,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z
-
小写: a , b , c , d , e , f , g , h , i , j , k , l , l , n , o , p , q , r , s , t , u , v , w , x , y , z \mathsf{a,b,c,d,e,f,g,h,i,j,k,l,l,n,o,p,q,r,s,t,u,v,w,x,y,z} a,b,c,d,e,f,g,h,i,j,k,l,l,n,o,p,q,r,s,t,u,v,w,x,y,z
打字机体:\mathtt{} --> typewriter type
-
大写: A , B , C , D , E , F , Z , H , I , J , K , L , M , N , O , P , Q , R , S , T , U , V , W , X , Y , Z \mathtt{A,B,C,D,E,F,Z,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z} A,B,C,D,E,F,Z,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z
-
小写: a , b , c , d , e , f , g , h , i , j , k , l , l , n , o , p , q , r , s , t , u , v , w , x , y , z \mathtt{a,b,c,d,e,f,g,h,i,j,k,l,l,n,o,p,q,r,s,t,u,v,w,x,y,z} a,b,c,d,e,f,g,h,i,j,k,l,l,n,o,p,q,r,s,t,u,v,w,x,y,z
2. 三角变换公式


行内与独行
- 行内公式:将公式插入到本行内,符号:
$公式内容$,如: x y z xyz xyz - 独行公式:将公式插入到新的一行内,并且居中,符号:
$$公式内容$$,如: x y z xyz xyz
上标、下标与组合
- 上标符号,符号:
^,如: x 4 x^4 x4 - 下标符号,符号:
_,如: x 1 x_1 x1 - 组合符号,符号:
{},如: 16 8 O 2 + 2 {16}_{8}O{2+}_{2} 168O2+2
汉字、字体与格式
- 汉字形式,符号:
\mbox{},如:KaTeX parse error: Undefined control sequence: \mbox at position 4: V_{\̲m̲b̲o̲x̲{初始}} - 字体控制,符号:
\displaystyle,如: x + y y + z \displaystyle \frac{x+y}{y+z} y+zx+y - 下划线符号,符号:
\underline,如: x + y ‾ \underline{x+y} x+y - 标签,符号
\tag{数字},如:KaTeX parse error: \tag works only in display equations - 上大括号,符号:
\overbrace{算式},如: a + b + c + d ⏞ 2.0 \overbrace{a+b+c+d}^{2.0} a+b+c+d 2.0 - 下大括号,符号:
\underbrace{算式},如: a + b + c ⏟ 1.0 + d a+\underbrace{b+c}_{1.0}+d a+1.0 b+c+d - 上位符号,符号:
\stacrel{上位符号}{基位符号},如: x ⃗ = d e f x 1 , … , x n \vec{x}\stackrel{\mathrm{def}}{=}{x_1,\dots,x_n} x =defx1,…,xn
占位符
- 两个quad空格,符号:
\qquad,如: x y x \qquad y xy - quad空格,符号:
\quad,如: x y x \quad y xy - 大空格,符号
\,如: x y x \ y x y - 中空格,符号
\:,如: x : y x : y x:y - 小空格,符号
\,,如: x , y x , y x,y - 没有空格,符号``,如: x y xy xy
- 紧贴,符号
\!,如: x ! y x ! y x!y
定界符与组合
- 括号,符号:
()\big(\big) \Big(\Big) \bigg(\bigg) \Bigg(\Bigg),如: ( ) ( ) ( ) ( ) ( ) ()\big(\big) \Big(\Big) \bigg(\bigg) \Bigg(\Bigg) ()()()()() - 中括号,符号:
[],如: [ x + y ] [x+y] [x+y] - 大括号,符号:
\{ \},如: x + y {x+y} x+y - 自适应括号,符号:
\left \right,如: ( x ) \left(x\right) (x), ( x y z ) \left(x{yz}\right) (xyz) - 组合公式,符号:
{上位公式 \choose 下位公式},如: ( n + 1 k ) = ( n k ) + ( n k − 1 ) {n+1 \choose k}={n \choose k}+{n \choose k-1} (kn+1)=(kn)+(k−1n) - 组合公式,符号:
{上位公式 \atop 下位公式},如: ∑ k 0 , k 1 , … > 0 k 0 + k 1 + ⋯ = n A k 0 A k 1 ⋯ \sum_{k_0,k_1,\ldots>0 \atop k_0+k_1+\cdots=n}A_{k_0}A_{k_1}\cdots ∑k0+k1+⋯=nk0,k1,…>0Ak0Ak1⋯
四则运算
- 加法运算,符号:
+,如: x + y = z x+y=z x+y=z - 减法运算,符号:
-,如: x − y = z x-y=z x−y=z - 加减运算,符号:
\pm,如: x ± y = z x \pm y=z x±y=z - 减甲运算,符号:
\mp,如: x ∓ y = z x \mp y=z x∓y=z - 乘法运算,符号:
\times,如: x × y = z x \times y=z x×y=z - 点乘运算,符号:
\cdot,如: x ⋅ y = z x \cdot y=z x⋅y=z - 星乘运算,符号:
\ast,如: x ∗ y = z x \ast y=z x∗y=z - 除法运算,符号:
\div,如: x ÷ y = z x \div y=z x÷y=z - 斜法运算,符号:
/,如: x / y = z x/y=z x/y=z - 分式表示,符号:
\frac{分子}{分母},如: x + y y + z \frac{x+y}{y+z} y+zx+y - 分式表示,符号:
{分子} \voer {分母},如: x + y y + z {x+y} \over {y+z} y+zx+y - 绝对值表示,符号:
||,如: ∣ x + y ∣ |x+y| ∣x+y∣
高级运算
- 平均数运算,符号:
\overline{算式},如: x y z ‾ \overline{xyz} xyz - 开二次方运算,符号:
\sqrt,如: x \sqrt x x - 开方运算,符号:
\sqrt[开方数]{被开方数},如: x + y 3 \sqrt[3]{x+y} 3x+y - 对数运算,符号:
\log,如: log ( x ) \log(x) log(x) - 极限运算,符号:
\lim,如: lim y → 0 x → ∞ x y \lim^{x \to \infty}_{y \to 0}{\frac{x}{y}} limy→0x→∞yx - 极限运算,符号:
\displaystyle \lim,如: lim y → 0 x → ∞ x y \displaystyle \lim^{x \to \infty}_{y \to 0}{\frac{x}{y}} y→0limx→∞yx - 求和运算,符号:
\sum,如: ∑ y → 0 x → ∞ x y \sum^{x \to \infty}_{y \to 0}{\frac{x}{y}} ∑y→0x→∞yx - 求和运算,符号:
\displaystyle \sum,如: ∑ y → 0 x → ∞ x y \displaystyle \sum^{x \to \infty}_{y \to 0}{\frac{x}{y}} y→0∑x→∞yx - 积分运算,符号:
\int,如: ∫ 0 ∞ x d x \int^{\infty}_{0}{xdx} ∫0∞xdx - 积分运算,符号:
\displaystyle \int,如: ∫ 0 ∞ x d x \displaystyle \int^{\infty}_{0}{xdx} ∫0∞xdx - 微分运算,符号:
\partial,如: ∂ x ∂ y \frac{\partial x}{\partial y} ∂y∂x - 矩阵表示,符号:
\begin{matrix} \end{matrix},如:KaTeX parse error: Undefined control sequence: \5 at position 38: …1 &2 &\cdots &4\̲5̲ &6 &\cdots &8\…
逻辑运算
- 等于运算,符号:
=,如: x + y = z x+y=z x+y=z - 大于运算,符号:
>,如: x + y > z x+y>z x+y>z - 小于运算,符号:
<,如: x + y < z x+y<z x+y<z - 大于等于运算,符号:
\geq,如: x + y ≥ z x+y \geq z x+y≥z - 小于等于运算,符号:
\leq,如: x + y ≤ z x+y \leq z x+y≤z - 不等于运算,符号:
\neq,如: x + y ≠ z x+y \neq z x+y=z - 不大于等于运算,符号:
\ngeq,如: x + y ≱ z x+y \ngeq z x+y≱z - 不大于等于运算,符号:
\not\geq,如: x + y ≱ z x+y \not\geq z x+y≥z - 不小于等于运算,符号:
\nleq,如: x + y ≰ z x+y \nleq z x+y≰z - 不小于等于运算,符号:
\not\leq,如: x + y ≰ z x+y \not\leq z x+y≤z - 约等于运算,符号:
\approx,如: x + y ≈ z x+y \approx z x+y≈z - 恒定等于运算,符号:
\equiv,如: x + y ≡ z x+y \equiv z x+y≡z
集合运算
- 属于运算,符号:
\in,如: x ∈ y x \in y x∈y - 不属于运算,符号:
\notin,如: x ∉ y x \notin y x∈/y - 不属于运算,符号:
\not\in,如: x ∉ y x \not\in y x∈y - 子集运算,符号:
\subset,如: x ⊂ y x \subset y x⊂y - 子集运算,符号:
\supset,如: x ⊃ y x \supset y x⊃y - 真子集运算,符号:
\subseteq,如: x ⊆ y x \subseteq y x⊆y - 非真子集运算,符号:
\subsetneq,如: x ⊊ y x \subsetneq y x⊊y - 真子集运算,符号:
\supseteq,如: x ⊇ y x \supseteq y x⊇y - 非真子集运算,符号:
\supsetneq,如: x ⊋ y x \supsetneq y x⊋y - 非子集运算,符号:
\not\subset,如: x ⊄ y x \not\subset y x⊂y - 非子集运算,符号:
\not\supset,如: x ⊅ y x \not\supset y x⊃y - 并集运算,符号:
\cup,如: x ∪ y x \cup y x∪y - 交集运算,符号:
\cap,如: x ∩ y x \cap y x∩y - 差集运算,符号:
\setminus,如: x ∖ y x \setminus y x∖y - 同或运算,符号:
\bigodot,如: x ⨀ y x \bigodot y x⨀y - 同与运算,符号:
\bigotimes,如: x ⨂ y x \bigotimes y x⨂y - 实数集合,符号:
\mathbb{R},如:\mathbb{R} - 自然数集合,符号:
\mathbb{Z},如:\mathbb{Z} - 空集,符号:
\emptyset,如: ∅ \emptyset ∅
数学符号
- 无穷,符号:
\infty,如: ∞ \infty ∞ - 虚数,符号:
\imath,如: ı \imath ı - 虚数,符号:
\jmath,如: ȷ \jmath ȷ - 数学符号,符号
\hat{a},如: a ^ \hat{a} a^ - 数学符号,符号
\check{a},如: a ˇ \check{a} aˇ - 数学符号,符号
\breve{a},如: a ˘ \breve{a} a˘ - 数学符号,符号
\tilde{a},如: a ~ \tilde{a} a~ - 数学符号,符号
\bar{a},如: a ˉ \bar{a} aˉ - 矢量符号,符号
\vec{a},如: a ⃗ \vec{a} a - 数学符号,符号
\acute{a},如: a ˊ \acute{a} aˊ - 数学符号,符号
\grave{a},如: a ˋ \grave{a} aˋ - 数学符号,符号
\mathring{a},如: a ˚ \mathring{a} a˚ - 一阶导数符号,符号
\dot{a},如: a ˙ \dot{a} a˙ - 二阶导数符号,符号
\ddot{a},如: a ¨ \ddot{a} a¨ - 上箭头,符号:
\uparrow,如: ↑ \uparrow ↑ - 上箭头,符号:
\Uparrow,如: ⇑ \Uparrow ⇑ - 下箭头,符号:
\downarrow,如: ↓ \downarrow ↓ - 下箭头,符号:
\Downarrow,如: ⇓ \Downarrow ⇓ - 左箭头,符号:
\leftarrow,如: ← \leftarrow ← - 左箭头,符号:
\Leftarrow,如: ⇐ \Leftarrow ⇐ - 右箭头,符号:
\rightarrow,如: → \rightarrow → - 右箭头,符号:
\Rightarrow,如: ⇒ \Rightarrow ⇒ - 底端对齐的省略号,符号:
\ldots,如: 1 , 2 , … , n 1,2,\ldots,n 1,2,…,n - 中线对齐的省略号,符号:
\cdots,如: x 1 2 + x 2 2 + ⋯ + x n 2 x_1^2 + x_2^2 + \cdots + x_n^2 x12+x22+⋯+xn2 - 竖直对齐的省略号,符号:
\vdots,如: ⋮ \vdots ⋮ - 斜对齐的省略号,符号:
\ddots,如: ⋱ \ddots ⋱
希腊字母
| 字母 | 实现 | 字母 | 实现 |
|---|---|---|---|
| A | A | α | \alhpa |
| B | B | β | \beta |
| Γ | \Gamma | γ | \gamma |
| Δ | \Delta | δ | \delta |
| E | E | ϵ | \epsilon |
| Z | Z | ζ | \zeta |
| H | H | η | \eta |
| Θ | \Theta | θ | \theta |
| I | I | ι | \iota |
| K | K | κ | \kappa |
| Λ | \Lambda | λ | \lambda |
| M | M | μ | \mu |
| N | N | ν | \nu |
| Ξ | \Xi | ξ | \xi |
| O | O | ο | \omicron |
| Π | \Pi | π | \pi |
| P | P | ρ | \rho |
| Σ | \Sigma | σ | \sigma |
| T | T | τ | \tau |
| Υ | \Upsilon | υ | \upsilon |
| Φ | \Phi | ϕ | \phi |
| X | X | χ | \chi |
| Ψ | \Psi | ψ | \psi |
| Ω | \v | ω | \omega |
3. 线性代数知识



































4. 反对称矩阵
反对称矩阵又称(斜对称矩阵)是一个方形矩阵,其转置矩阵和自身的加法逆元相等。
A
t
o
p
=
−
A
(1.1)
A^{\\top} = -A \tag{1.1}
Atop=−A(1.1)
或写作
A
=
(
a
i
j
)
A=(a_{ij})
A=(aij),各元素的关系为:
a
i
j
=
−
a
j
i
(1.2)
a_{ij} = -a_{ji} \tag{1.2}
aij=−aji(1.2)
例如,下例为一个反对称矩阵:
[
0
2
−
1
−
2
0
−
4
1
4
0
]
(1.3)
\begin{bmatrix} 0 & 2 & -1 \\ -2 & 0 & -4 \\ 1 & 4 & 0 \\ \end{bmatrix} \tag{1.3}
0−21204−1−40
(1.3)
在SLAM学习中,一个向量可以映射到一个反对称矩阵,从向量到反对称矩阵的映射符号通常用
^
\hat{}
^ 符号来表示,比如对于向量
a
=
[
a
1
,
a
2
,
a
3
]
⊤
a = [a_1,a_2,a_3]^{\top}
a=[a1,a2,a3]⊤,其反对称矩阵为:
a
∧
=
A
=
[
0
−
a
3
a
2
a
3
0
−
a
1
−
a
2
a
1
0
]
(1.4)
a^{\wedge}=A= \begin{bmatrix} 0 & -a_3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \\ \end{bmatrix} \tag{1.4}
a∧=A=
0a3−a2−a30a1a2−a10
(1.4)
另外一个小tips,反对称符号在latex的表示为\hat{}或者\wedge。
4.2. 反对称矩阵与叉乘
设有向量
a
=
[
a
1
,
a
2
,
a
3
]
⊤
a = [a_1,a_2,a_3]^\top
a=[a1,a2,a3]⊤和
b
=
[
b
1
,
b
2
,
b
3
]
⊤
b = [b_1,b_2,b_3]\top
b=[b1,b2,b3]⊤,则叉乘和反对称化的关系如下:
a
×
b
=
a
∧
b
(2.1)
a \times b = a^\wedge b \tag{2.1}
a×b=a∧b(2.1)
以及反交换律:
a
∧
b
=
−
b
∧
a
(2.2)
a^\wedge b = -b^\wedge a \tag{2.2}
a∧b=−b∧a(2.2)
a
⊤
b
∧
=
−
b
⊤
a
∧
(2.3)
a^\top b^\wedge = -b^\top a^\wedge \tag{2.3}
a⊤b∧=−b⊤a∧(2.3)
同时有以下性质成立:
(
a
∧
b
)
∧
=
(
a
×
b
)
∧
=
a
∧
b
∧
−
b
∧
a
∧
(2.4)
(a^\wedge b)^\wedge = (a \times b)^\wedge = a^\wedge b^\wedge - b^\wedge a^\wedge \tag{2.4}
(a∧b)∧=(a×b)∧=a∧b∧−b∧a∧(2.4)
4.3 反对称矩阵的行列式
若A是
n
×
n
n \times n
n×n的反对称矩阵,其行列式满足:
d
e
t
(
A
)
=
d
e
t
(
A
⊤
)
=
d
e
t
(
−
A
)
=
(
−
1
)
n
d
e
t
(
A
)
(3.1)
det(A) = det(A^\top)=det(-A)=(-1)^ndet(A) \tag{3.1}
det(A)=det(A⊤)=det(−A)=(−1)ndet(A)(3.1)
- 如果n是奇数,行列式等于0。这个结果叫雅克比定理。
- 若n是偶数,行列式可以写成部分元素的多项式的平方,这个称为Pfaffian行列式。
4.4 反对称矩阵的乘法
4.4.1 反对称矩阵连乘
假设向量
a
=
[
a
1
,
a
2
,
a
3
]
⊤
a = [a_1,a_2,a_3]^\top
a=[a1,a2,a3]⊤,其为单位向量,即
a
1
2
+
a
2
2
+
a
3
2
=
1
\sqrt{a^2_1 + a^2_2 + a^2_3} = 1
a12+a22+a32=1,则易推出:
a
∧
a
∧
=
a
a
⊤
−
I
(4.1)
a^\wedge a^\wedge = aa^\top - I \tag{4.1}
a∧a∧=aa⊤−I(4.1)
继续连乘:
a
∧
a
∧
a
∧
=
−
a
∧
(4.2)
a^\wedge a^\wedge a^\wedge = -a^\wedge \tag{4.2}
a∧a∧a∧=−a∧(4.2)
更多的连乘可以用以上规律进行推导。

4.4.2 反对称矩阵与矩阵相乘
定义向量
u
=
(
u
1
,
u
2
,
u
3
)
⊤
u = (u_1, u_2, u_3)^\top
u=(u1,u2,u3)⊤和任意矩阵C,则有如下公式成立:
(
C
u
)
∧
=
C
u
∧
C
⊤
(4.3)
(Cu)^\wedge = Cu^\wedge C^\top \tag{4.3}
(Cu)∧=Cu∧C⊤(4.3)
4.5 反对称矩阵的加法
设有向量
a
=
[
a
1
,
a
2
,
a
3
]
⊤
a = [a_1,a_2,a_3]^\top
a=[a1,a2,a3]⊤和
b
=
[
b
1
,
b
2
,
b
3
]
⊤
b = [b_1,b_2,b_3]\top
b=[b1,b2,b3]⊤,则有运算:
a
∧
+
b
∧
=
(
a
+
b
)
∧
(5.1)
a^\wedge + b^\wedge = (a+b)^\wedge \tag{5.1}
a∧+b∧=(a+b)∧(5.1)
4.6 无穷小旋转
斜对称矩阵形成了正交群O(n)在单位矩阵的切空间。在某种意义上,斜对称矩阵可以视无穷小旋转。
另外一种说法是,斜对称矩阵的空间形成了李群O(n)的李代数o(n)。这个空间上的李括号由交换子给出:
[
A
,
B
]
=
A
B
−
B
A
(6.1)
[A,B] = AB -BA \tag{6.1}
[A,B]=AB−BA(6.1)
很容易验证,两个斜对称矩阵的交换子也是斜对称的。
于是,斜对称矩阵A的矩阵指数,是正交矩阵R:
R
=
e
x
p
(
A
)
=
∑
n
=
0
∞
A
n
n
!
(6.2)
R =exp(A) = \sum^\infty_{n=0} \frac{A^n}{n!} \tag{6.2}
R=exp(A)=n=0∑∞n!An(6.2)
李代数的指数映射的像总是位于含有单位元的李群的连通分支内。在李群O(n)的情况中,这个连通分支是特殊正交群SO(n),由所有行列式为1的正交矩阵组成。因此
_
R
_
=
e
x
p
(
_
A
_
)
\_R\_ = exp(\_A\_)
_R_=exp(_A_)的行列式为+1。于是,每一个行列式为1的正交矩阵都可以写成某个斜对称矩阵的指数。
5. SLAM中常用的矩阵变换
5.1 行矩阵、列矩阵
m × n m×n m×n阶矩阵中, m = 1 m=1 m=1称为行矩阵,也称为 n n n维行向量; n = 1 n=1 n=1称为列矩阵,也称为 m m m维列向量。
5.2 矩阵的转置
假设A和B是两个 m × n m \times n m×n的矩阵, λ \lambda λ是一个常数,有:
- ( A T ) T = A (A^T)^T=A (AT)T=A
- ( A B ) T = B T A T , ( A B ) − 1 = B − 1 A − 1 (AB)^{T} = B^{T}A^T,(AB)^{-1} = B^{-1}A^{-1} (AB)T=BTAT,(AB)−1=B−1A−1
- ( A + B ) T = A T + B T (A+B)^T=A^T+B^T (A+B)T=AT+BT
- ( λ A ) T = λ A T (\lambda A)^T=\lambda A^T (λA)T=λAT
- ( A T ) − 1 = ( A − 1 ) T (A^T)^{-1}= (A^{-1})^T (AT)−1=(A−1)T
对转置矩阵求导 :
d
x
T
d
x
=
I
\frac{dx^T}{dx}= I
dxdxT=I
(
A
x
)
T
d
x
=
A
T
\frac{(Ax)^T}{dx}= A^T
dx(Ax)T=AT
5.3 奇异矩阵
奇异矩阵和非奇异矩阵首先是方阵,其次奇异矩阵的秩不是满秩,即 ∣ A ∣ = 0 |A|=0 ∣A∣=0
5.4 对称矩阵与反对称矩阵
设 A A A是 n n n阶方阵,如果 A T = A A^T=A AT=A,则称 A A A是对称矩阵。如果 A T = − A A^T=-A AT=−A,则称 A A A为反对称矩阵。反对称矩阵中,主对角线上的元素均为0。
- ( A B ) T = B T A T (AB)^T=B^TA^T (AB)T=BTAT
5.5 正定矩阵
正定矩阵:
- 广义定义: 设 M M M是 n n n阶方阵,如果对任何非零向量 z z z,都有 z T M z > 0 z^TMz>0 zTMz>0,就称M为正定矩阵
- 性质:
- 正定矩阵的行列式恒为正
- 若 A A A是正定矩阵,则 A T A^T AT也是正定矩阵
- 两个正定矩阵的和是正定矩阵
- 正实数与正定矩阵的乘积是正定矩阵
- 正定矩阵的特征值均为正
- 正定矩阵存在实可逆矩阵l,使得 A = l T l A=l^Tl A=lTl
- 正定矩阵存在秩为 m x n mxn mxn的实矩阵 l l l,使得 A = l T l A=l^Tl A=lTl
- 正定矩阵存在主对角元素全为正的实三角元素R,使得 A = l T l A=l^Tl A=lTl
M M M为正定矩阵 < = > x T M x > 0 <=> x^TMx > 0 <=>xTMx>0for all x ∈ R n x \in \mathbb R^n x∈Rn
M M M为半正定矩阵 < = > x T M x ⩾ 0 <=> x^TMx \geqslant 0 <=>xTMx⩾0for all x ∈ R n x \in \mathbb R^n x∈Rn
5.5.1 对称正定矩阵
设 A ∈ R n × n A \in R^ {n\times n} A∈Rn×n,若 A = A T A=A^T A=AT,对任意 0 ≠ X ∈ R n 0\not=X \in R^n 0=X∈Rn,都有 X T A X > 0 X^TAX>0 XTAX>0,则称A为对称正定矩阵
5.6 实对称矩阵
实对称矩阵是一个方阵,其转置等于自身的矩阵。换句话说,如果一个矩阵 A A A 满足 A = A ⊤ A = A^\top A=A⊤,那么它就是实对称矩阵。
-
特征值分解:
对于实对称矩阵 (A),可以通过特征值分解得到:
[
A = Q \Lambda Q^\top
]
其中,(Q) 是正交矩阵,列向量是 (A) 的特征向量,(\Lambda) 是对角矩阵,对角线上的元素是 (A) 的特征值。 -
特征值的性质:
- 实对称矩阵的特征值都是实数。
- 实对称矩阵的特征值互不相同(可以有重复的特征值,但对应的特征向量不同)。
-
正交性质:
实对称矩阵的特征向量相互正交。也就是说,如果 A A A 的特征向量 v i v_i vi 和 v j v_j vj 对应的特征值不同(或者重复但线性无关),则它们正交。 -
谱范数:
实对称矩阵的谱范数等于最大特征值的绝对值。即,如果 A A A 的特征值为 λ 1 , λ 2 , . . . , λ n \lambda_1, \lambda_2, ..., \lambda_n λ1,λ2,...,λn,则
∣ ∣ A ∣ ∣ 2 = max i ∣ λ i ∣ ||A||_2 = \max_{i} |\lambda_i| ∣∣A∣∣2=maxi∣λi∣ -
对角化:
实对称矩阵可以通过正交相似变换对角化。具体而言,如果 A A A 是一个 n × n n \times n n×n 的实对称矩阵,那么存在一个正交矩阵 P P P,使得 P ⊤ A P P^\top A P P⊤AP 是一个对角矩阵。 -
特殊矩阵形式:
实对称矩阵的一些特殊形式也有其特定的性质和公式,例如三对角矩阵、对角占优矩阵等。
5.7 伴随矩阵
设矩阵 A A A中, A i j A_{ij} Aij为行列式 ∣ A ∣ |A| ∣A∣中元素 a i j a_{ij} aij的代数余子式,称 A ∗ A^* A∗为矩阵 A A A的伴随矩阵。
- A A ∗ = A ∗ A = ∣ A ∣ E AA^*=A^*A=|A|E AA∗=A∗A=∣A∣E
- ( A ∗ ) T = ( A T ) ∗ , ( k A ) ∗ = k n − 1 A ∗ (A^*)^T=(A^T)^*, (kA)^*=k^{n-1}A^* (A∗)T=(AT)∗,(kA)∗=kn−1A∗
设 A A A可逆:
- A ∗ = ∣ A ∣ A − 1 A^*=|A|A^{-1} A∗=∣A∣A−1
- ( A ∗ ) − 1 = ( A − 1 ) ∗ = ∣ A ∣ − 1 A (A^*)^{-1}=(A^{-1})^*=|A|^{-1}A (A∗)−1=(A−1)∗=∣A∣−1A
- ( A B ) ∗ = B ∗ A ∗ (AB)^*=B^*A^* (AB)∗=B∗A∗
- ( A ∗ ) ∗ = ∣ A ∣ n − 2 A (A^*)^*=|A|^{n-2}A (A∗)∗=∣A∣n−2A
5.8 正交阵
正交可以理解为垂直
正交阵是指满足
A
A
T
=
E
AA^T=E
AAT=E或者
A
T
A
=
E
A^T A=E
ATA=E的
n
n
n阶方阵
A
A
A,其中
E
E
E为n阶单位阵。
$
A
A
T
=
[
α
_
1
α
2
.
.
.
α
n
]
[
α
1
T
α
2
T
.
.
.
α
n
T
]
=
[
α
1
α
1
T
α
1
α
2
T
.
.
.
α
1
α
n
T
α
2
α
1
T
α
2
α
2
T
.
.
.
α
2
α
n
T
.
.
.
α
n
α
1
T
α
n
α
2
T
.
.
.
α
n
α
n
T
]
=
[
1
0
.
.
.
0
0
1
.
.
.
0
.
.
.
0
0
.
.
.
1
]
=
E
AA^T = \begin{bmatrix} \alpha\_1\\ \alpha_2\\ .\\ .\\ .\\ \alpha_n\\ \end{bmatrix}\begin{bmatrix} \alpha_1^T && \alpha_2^T && ... && \alpha_n^T \end{bmatrix} =\begin{bmatrix} \alpha_1 \alpha_1^T && \alpha_1 \alpha_2^T && ... && \alpha_1 \alpha_n^T\\ \alpha_2 \alpha_1^T && \alpha_2 \alpha_2^T && ... && \alpha_2 \alpha_n^T\\ .\\ .\\ .\\ \alpha_n \alpha_1^T && \alpha_n \alpha_2^T && ... && \alpha_n \alpha_n^T\\ \end{bmatrix} =\begin{bmatrix} 1&& 0 && ... && 0\\ 0 && 1 && ... && 0\\ .\\ .\\ .\\ 0 && 0 && ... && 1\\ \end{bmatrix} = E
AAT=
α_1α2...αn
[α1Tα2T...αnT]=
α1α1Tα2α1T...αnα1Tα1α2Tα2α2Tαnα2T.........α1αnTα2αnTαnαnT
=
10...0010.........001
=E
如果矩阵的各列向量都是单位向量,并且两两正交。那么就说这个矩阵是正交矩阵。
- 性质:
设A是n阶正交阵,则
- A T = A − 1 A^T = A^{-1} AT=A−1
- A T A = A A T = E A^TA=AA^T=E ATA=AAT=E( E E E是 n n n阶单位阵);
- 若 A A A是正交阵,则 A T A^T AT或 A − 1 A^{-1} A−1亦是正交阵;
- 若 A 、 B A、B A、B是正交阵,则 A B AB AB亦是正交阵;
- ∣ A ∣ = 1 |A|=1 ∣A∣=1或 ∣ A ∣ = − 1 |A|=-1 ∣A∣=−1;
- 实对称阵的对应不同特征值的特征向量正交;
- 凡是正交矩阵,一定可以对角化。
对角化:参考相似矩阵,本质就是 A = P − 1 B P A=P^{-1}BP A=P−1BP , 也就是说一个矩阵A可以转为一个对角阵B.
正交矩阵:本身就是相互垂直,只是说它不见得是各个标准轴。以三维空间为例,我们希望正交矩阵是:

但是实际他很可能为下边这个样子
 亦即以z轴为中心逆时针旋转了45°, 此时向量a,b,c依然相互正交,但是其列向量并不都在标准轴上.
亦即以z轴为中心逆时针旋转了45°, 此时向量a,b,c依然相互正交,但是其列向量并不都在标准轴上.
即正交阵是一个在三维坐标系中歪着摆的立方体,对角化就是把这个立方体摆正回来(也就是让它的某个顶点放在原点上,同时这个原点的三条边正好对在三维坐标系xyz三个轴上)
5.9 准对角形矩阵
设 A A A为 n n n阶方阵,如果它的分块矩阵具有如下形式: [ A 1 0 . . . 0 0 A 2 . . . 0 . . . 0 0 . . . A n ] \begin{bmatrix} A_1&0&...&0\\ 0&A_2&...& 0\\ ...\\ 0&0&...&A_n\\ \end{bmatrix} A10...00A20.........00An 则称 A A A为准对角形矩阵。
[ A 1 0 . . . 0 0 A 2 . . . 0 . . . 0 0 . . . A _ n ] − 1 = [ A 1 − 1 0 . . . 0 0 A 2 − 1 . . . 0 . . . 0 0 . . . A n − 1 ] \begin{bmatrix}A_1&0&...&0\\0&A_2&...& 0\\ ...\\0&0&...&A\_n\\ \end{bmatrix}^{-1} = \begin{bmatrix}A_1^{-1}&0&...&0\\0&A_2^{-1}&...& 0\\ ...\\0&0&...&A_n^{-1}\\\end{bmatrix} A10...00A20.........00A_n −1= A1−10...00A2−10.........00An−1
[ A 1 0 . . . 0 0 A 2 . . . 0 . . . 0 0 . . . A n ] − 1 = [ A 1 − 1 0 . . . 0 0 A 2 − 1 . . . 0 . . . 0 0 . . . A _ n − 1 ] \begin{bmatrix}A_1&0&...&0\\0&A_2&...& 0\\ ...\\0&0&...&A_n\\\end{bmatrix}^{-1} = \begin{bmatrix}A_1^{-1}&0&...&0\\0&A_2^{-1}&...& 0\\ ...\\0&0&...&A\_n^{-1}\\\end{bmatrix} A10...00A20.........00An −1= A1−10...00A2−10.........00A_n−1
5.10 矩阵求导
5.11 矩阵运算规则
设 A = ( a i j ) m × n , B = ( b i j ) n × l A=(a_{ij})_{m\times n},B=(b_{ij})_{n\times l} A=(aij)m×n,B=(bij)n×l,则对于A与B的乘积 C = A B C=AB C=AB有:
C C C的第 i i i行第 j j j列元素 c i j c_{ij} cij由 A A A的第 i i i行元素与 B B B的第 j j j列元素对应相乘,再取乘积之和
5.12 n阶方阵
m × n m×n m×n阶矩阵 A A A中, m = n m=n m=n;
n n n阶方阵 A A A,可定义行列式记为 ∣ A ∣ |A| ∣A∣;
n n n阶方阵存在主对角线及主对角线元素。
- ∣ A B ∣ = ∣ A ∣ ∣ B ∣ |AB|=|A||B| ∣AB∣=∣A∣∣B∣
- ∣ A 1 A 2 . . . A n ∣ = ∣ A 1 ∣ ∣ A 2 ∣ . . . ∣ A n ∣ |A_1A_2...A_n|=|A_1||A_2|...|A_n| ∣A1A2...An∣=∣A1∣∣A2∣...∣An∣
- ∣ A T ∣ = ∣ A ∣ , ∣ A − 1 ∣ = ∣ A ∣ − 1 |A^T|=|A|,|A^{-1}|=|A|^{-1} ∣AT∣=∣A∣,∣A−1∣=∣A∣−1
- ∣ k A ∣ n = k n ∣ A ∣ |kA|_n=k^n|A| ∣kA∣n=kn∣A∣
- ∣ A ∗ ∣ n = ∣ A ∣ n − 1 |A^*|_n=|A|^{n-1} ∣A∗∣n=∣A∣n−1
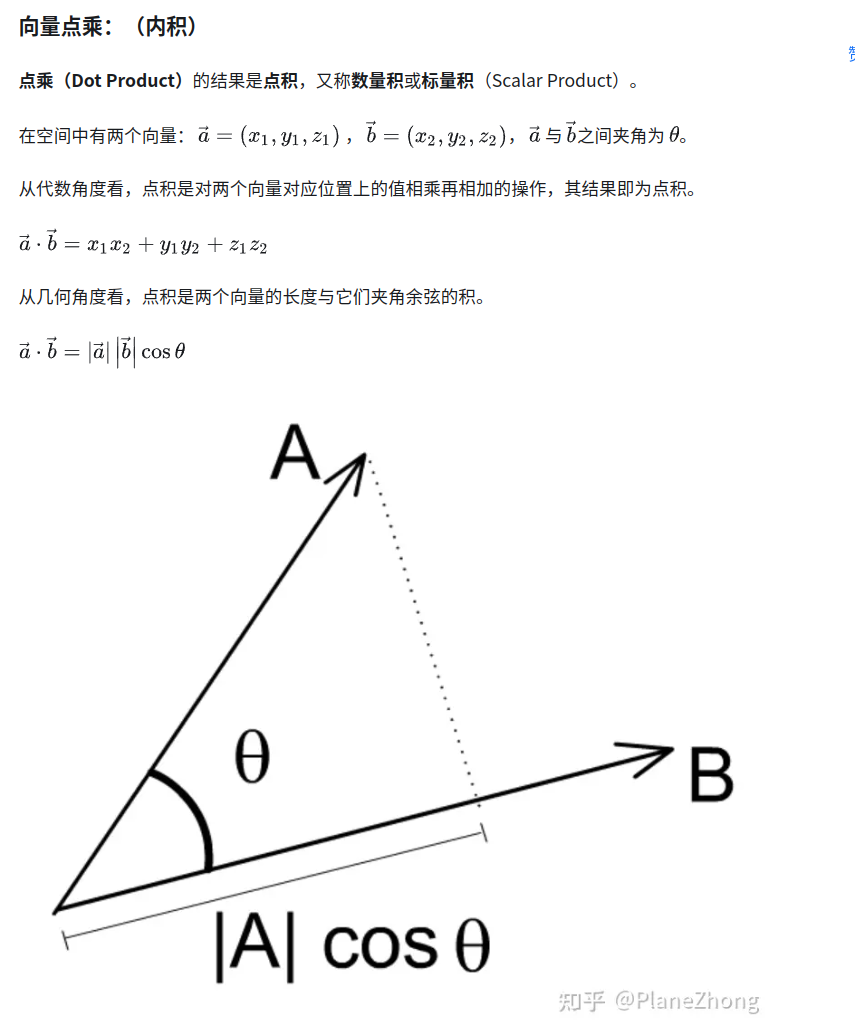
5. 点乘叉乘

6. 参考链接
https://blog.csdn.net/YEN_CSDN/article/details/79966985
https://blog.csdn.net/shyjhyp11/article/details/125458690
https://mp.weixin.qq.com/s/gDLwWhWOjg-bZXPQ9mdkHg
https://blog.csdn.net/sdnuwjw/article/details/119920649
https://su-lemon.gitee.io/post/73a19565.html
https://blog.csdn.net/CSSDCC/article/details/121653596
https://blog.csdn.net/weixin_45626706/article/details/126333057

























 6969
6969

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










