简介
继上节8说到利用手动构建的语法树解析下面的c语言代码:
a = 1
sum = 0
input(x)
while(a <= x){
sum = sum + a
a = a+1;
}
print(sum)而一个编译器不应该依赖用户去手动构建对应语言的语法树,我们需要的是一种支持自动构建语法树的策略。本节将要说明的就是如何利用前面1-6节学到的lex,yacc以及符号表,7-8节学到的语法树来支持给定c语言代码自动构建过程。
动机
在第5节变量支持的计算器中,对于expr的语法解析有如下的yacc代码:
lines : lines expr EOL { printf("%g\n", $2); }
| lines EOL
| lines COMMENT
|
;
expr : expr PLUS expr { $$ = $1 + $3; }
| expr MINUS expr { $$ = $1 - $3; }
| expr TIMES expr { $$ = $1 * $3; }
| expr OVER expr { $$ = $1 / $3; }
| LP expr RP { $$ = $2; }
| '-' expr %prec UMINUS { $$ = -$2; }
| NUMBER {
$$=$1;} //$$=$1 can be ignored
| ID {
$$ = sym_table.getValue($1);}//get value from sym_table
| ID ASSIGN expr {sym_table.setValue($1, $3); $$=$3; }//modify the value已经知道的是上面每一行都是对应的语法匹配规则(例如expr PLUS expr)以及当规则匹配后要执行的动作(位于{}中,例如$$ = $1 + $3;)。如果将上面要执行的动作修改为创建对应的语法表达式节点,不就可以实现自动构建语法树了吗? 针对上面的expr PLUS expr,其对应的动作可以修改为
$$ = expr.NewRoot(EXPR_NODE, OP_EXPR, NodeAttr(PLUS), Integer, $1, $3);同理,其他语法规则的执行动作也可以进行相应的修改,这样当一个表达式语法分析完毕后,对应的表达式语法树也就构建完成了。
总体概览
- lex和yacc进行相应的词法,语法分析,并构建对应的语法树
- tree.h和tree.cpp用来支撑语法树的构建过程,提供相应的创建函数,被yacc使用
- symtable.h和symtable.cpp用来支撑符号表的构建过程,提供符号表的创建,访问,修改等操作,用于支持变量以及可能的函数扩展。
- 只支持最基本的c语言,也就是第8节已经进行测试过的。总述如下:变量,变量赋值,算术逻辑等运算,if语句,while语句,输入输出语句,表达式语句,复合语句(不支持变量声明,变量名出现的第一次开始将其加入到符号表,默认值为0,使用赋值运算符可对变量值进行修改)。
可支持如下的代码:
其为迭代法解一元二次方程组,方程的三个参数为a,b,c。
main()
{
//求解X1,在曲线对称轴处选择初始点
//x^2+3x+2 = 0
a = 1;
b = 3;
c = 2;
accuracy = 0.00001;
index=(-1.0*b)/(2*a);
if(b!=0)//b不等于0时进行迭代
{
temp=index;
index=-1.0*(a*temp*temp+c)/b;
while((fabs(index-temp))>accuracy)
{
temp=index;
index=-1.0*(a*temp*temp+c)/b;
}
x1=index;
x2=(-1.0*b)/a-x1;
}
else//b=0时ax^2+c=0直接求解
{
x1=sqrt(-1.0*c/a);
x2=-x1;
}
output(x1);
output(x2);
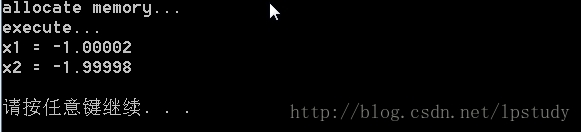
}编译器输出结果
lex文件源代码以及解析
前面所述,lex文件完成的词法解析的工作。 它将输入的字符串进行拆分成一个个的token,然后返回相应的token类型,将其传入到yacc中。例如:
letter [a-zA-Z]
digit [0-9]
id {letter}({letter}|{digit})*上述三行lex代码定义了三种token,字母,数字以及标示符。
lex在解析c语言代码时候,如果遇到相应的token,会向执行token中预定义的动作,例如:
{
id} {
int p = sym_table.lookup(yytext);
if(p == -1){
//not find
p = sym_table.insert(yytext);//insert the default value 0.0
}
yylval = &dummy;
yylval->attr.symtbl_seq = p;//return the position
return ID;
}
{number} {
yylval = &dummy;
yylval->attr.vali = atof(yytext);
return NUMBER;
}上述代码显得有些复杂了。id是标示符的解析,yytext是已经切分的token,首先向符号表sym_table中查找yytext,如果没有找到,那么将其插入到符号表;如果找到,直接返回此yytext对应的符号表的索引位置p。 随后对yylval赋值,并设置它的符号表的序号为p,最后返回ID,表明它是一个标示符。 注意p要被yacc所用,例如当碰到a=2,这个赋值动作是在yacc中进行分析的,在yacc构建语法树的时候,必须能够得到a这个标示符,然而lex仅仅返回了ID标示符,但lex通过yylval这个变量间接告诉了yacc词法解析器,此ID确切的内容,即是a。 如果id能够完全理解,那么number就更简单了,直接使用atof函数将字符串转换为double值,并赋值给yylval。
你可能有疑问yacc在哪里使用的yylval呢? 下面给出一小段yacc的代码,作为引子:
var : ID { $$ = createId(parser_tree, (int)($1->attr.symtbl_seq));} //$1 stores yylval, returned by lex.l上面的是yacc语法分析动作,当碰到ID标示符的时候,调用createId创建一个Node节点,并传入$1->attr.symtbl_seq。 $1就是lex中构造的yylval,这里直接使用它的符号表的序号。
下面是完整的lex代码:
%{
//this code will be added into the header of generated .cpp file
#include <iostream>
#include "sym_table.h"
#include "yacc.h"
#include "tree.h"
using namespace std;
int lineno = 1;
Node dummy;
//already defined in yacc.y, use %token...
//enum{LT, EQ, GT, IF, ELSE, ID, NUMBER, PLUS, MINUS, TIMES, OVER, INT, DOUBLE,CHAR, LP,RP};
const char* tokenStr[] = {
"LT", "EQ", "GT", "IF", "ELSE", "ID", "NUMBER", "PLUS", "MINUS", "TIMES", "OVER", "INT", "DOUBLE","CHAR"};
static void print_token(int token, char* lex);
%}
%name lexer
delim [ \t]
ws {delim}+
letter [a-zA-Z]
digit [0-9]
id {letter}({letter}|{digit})*
/* can support 12.34 */
number -?{digit}+(\.{digit}+)?
//(-?[1-9]+[0-9]*)|(-?[1-9])|0
%%
%{
//this code will be added into yyaction function
YYSTYPE YYFAR& yylval = *(YYSTYPE YYFAR*)yyparserptr->yylvalptr;
%}
{ws} {
/* do nothing */}
"int" {print_token(INT, yytext); return INT;}
"double" {print_token(DOUBLE, yytext);}
"char" {print_token(CHAR, yytext);}
";" {
return SEMICOLON;}
"," {
return COMMA;}
"+" {print_token(PLUS, yytext); return PLUS;}
"-" {print_token(MINUS, yytext); return MINUS;}
"*" {print_token(TIMES, yytext); return TIMES;}
"/" {print_token(OVER, yytext); return OVER;}
"(" {
return LP;}
")" {
return RP;}
"<" {
return LT;}
">" {
return GT;}
"<=" {
return LE;}
">=" {
return GE;}
"==" {
return EQ;}
"!=" {
return NE;}
"\n" {lineno++;}
"=" {
return ASSIGN;}
"if" {
return IF;}
"else" {
return ELSE;}
"while" {
return WHILE;}
"input" {
return INPUT;}
"output" {
return OUTPUT;}
"main" {
return MAIN;}
"$" {
return END;}
"{" {print_token(LBRACE, yytext); return LBRACE;}
"}" {print_token(RBRACE, yytext); return RBRACE;}
"||" {print_token(OR, yytext); return OR;}
"&&" {print_token(AND, yytext); return AND;}
"!" {print_token(NOT, yytext); return NOT;}
"sqrt" {
return SQRT;}
"fabs" {
return FABS;}
{id} {
int p = sym_table.lookup(yytext);
if(p == -1){
//not find
p = sym_table.insert(yytext);//insert the default value 0.0
}
yylval = &dummy;
yylval->attr.symtbl_seq = p;//return the position
return ID;
}
{number} {
yylval = &dummy;
yylval->attr.vali = atof(yytext);








 本文介绍了如何使用编译原理中的lex、yacc和符号表,结合手动构建的语法树,来自动解析和构建C语言代码的语法树。详细讲解了词法分析、语法分析、符号表管理和yacc的规则执行,提供了编译器的运行流程和代码示例。
本文介绍了如何使用编译原理中的lex、yacc和符号表,结合手动构建的语法树,来自动解析和构建C语言代码的语法树。详细讲解了词法分析、语法分析、符号表管理和yacc的规则执行,提供了编译器的运行流程和代码示例。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 4838
4838

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








