http://www.cppblog.com/MiYu/archive/2010/08/07/122573.html
http://blog.sina.com.cn/s/blog_7064e7850100y1xf.html
http://blog.csdn.net/duanruibupt/article/details/6869431
Catalan数问题的一个变形:
n+m个人排队买票,并且满足 ,票价为50元,其中n个人各手持一张50元钞票,m个人各手持一张100元钞票,除此之外大家身上没有任何其他的钱币,并且初始时候售票窗口没有钱,问有多少种排队的情况数能够让大家都买到票。
,票价为50元,其中n个人各手持一张50元钞票,m个人各手持一张100元钞票,除此之外大家身上没有任何其他的钱币,并且初始时候售票窗口没有钱,问有多少种排队的情况数能够让大家都买到票。
这个题目是Catalan数的变形,不考虑人与人的差异,如果m=n的话那么就是我们初始的Catalan数问题,也就是将手持50元的人看成是+1,手持100元的人看成是-1,任前k个数值的和都非负的序列数。
这个题目区别就在于n>m的情况,此时我们仍然可以用原先的证明方法考虑,假设我们要的情况数是 ,无法让每个人都买到的情况数是
,无法让每个人都买到的情况数是 ,那么就有
,那么就有 ,此时我们求
,此时我们求 ,我们假设最早买不到票的人编号是k,他手持的是100元并且售票处没有钱,那么将前k个人的钱从50元变成100元,从100元变成50元,这时候就有n+1个人手持50元,m-1个手持100元的,所以就得到
,我们假设最早买不到票的人编号是k,他手持的是100元并且售票处没有钱,那么将前k个人的钱从50元变成100元,从100元变成50元,这时候就有n+1个人手持50元,m-1个手持100元的,所以就得到 ,于是我们的结果就因此得到了,表达式是
,于是我们的结果就因此得到了,表达式是 。
。
1:给定n个数,有多少种出栈序列?
(问题的形象描述:
饭后,姐姐洗碗,妹妹把姐姐洗过的碗一个一个放进碗橱摞成一摞。一共有n个不同的碗,洗前也是摞成一摞的,也许因为小妹贪玩而使碗拿进碗橱不及时,姐姐则把洗过的碗摞在旁边,问:小妹摞起的碗有多少种可能的方式?
一个有n个1和n个-1组成的字串,且前k个数的和均不小于0,那这种字串的总数为多少?
P=A1A2A3……An,依据乘法结合律,不改变其顺序,只用括号表示成对的乘积,试问有几种括号化的方案?)
2:n个节点的二叉树有多少种构型?
3:有n+1个叶子的满二叉树的个数?

4:在n*n的格子中,只在下三角行走,每次横或竖走一格,有多少中走法?

5:将一个凸n+2边形区域分成三角形区域的方法数?

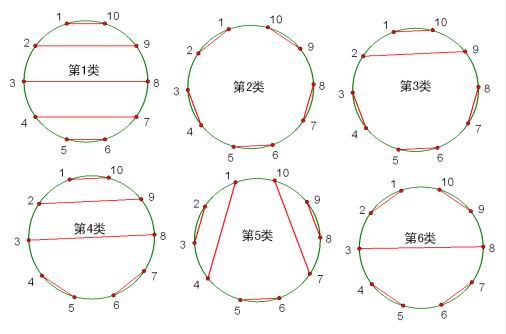
6:在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数?
7:用n个长方形填充一个高度为n的阶梯状图形的方法个数?

上面一些问题有些是同构的,但有些却实在看不出联系来,他们的答案却都为卡特兰数。在《Enumerative Combinatorics》一书中,竟然提到了多达 66种组合问题和卡特兰数有关。
我们先来看看何为卡特兰数:
卡塔兰数的一般项公式为 
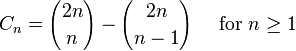
递归式:令h(0)=1,h(1)=1,catalan数满足递归式:
h(n)= 
另类递归式:
前几项为 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, ...
卡塔兰数的渐近增长为

1.括号化问题。
矩阵链乘: P=a1×a2×a3×……×an,依据乘法结合律,不改变其顺序,只用括号表示成对的乘积,试问有几种括号化的方案?(h(n)种)
2.出栈次序问题。
一个栈(无穷大)的进栈序列为1,2,3,..n,有多少个不同的出栈序列?
类似:
(1)有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票,另外n人只有10元钞票,剧院无其它钞票,问有多少中方法使得只要有10元的人买票,售票处就有5元的钞票找零?(将持5元者到达视作将5元入栈,持10元者到达视作使栈中某5元出栈)
(2)在圆上选择2n个点,将这些点成对连接起来,使得所得到的n条线段不相交的方法数。
3.将多边行划分为三角形问题。
将一个凸多边形区域分成三角形区域的方法数?
类似:一位大城市的律师在她住所以北n个街区和以东n个街区处工作。每天她走2n个街区去上班。如果她
从不穿越(但可以碰到)从家到办公室的对角线,那么有多少条可能的道路?
类似:在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数?
4.给顶节点组成二叉树的问题。
给定N个节点,能构成多少种形状不同的二叉树?
(一定是二叉树!
先去一个点作为顶点,然后左边依次可以取0至N-1个相对应的,右边是N-1到0个,两两配对相乘,就是h(0)*h(n-1) + h(2)*h(n-2) +  + h(n-1)h(0)=h(n))
+ h(n-1)h(0)=h(n))
(能构成h(N)个)








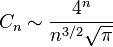
















 1126
1126

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








