参考『http://stat-design.blogspot.sg/search?updated-min=2011-01-01T00:00:00-06:00&updated-max=2012-01-01T00:00:00-06:00&max-results=4』
We know that the Mean gives us the central tendency of the data, the Standard Deviation explains the dispersion about the Mean, the Skewness represents the symmetry/asymmetry of the data, and the Kurtosis is related to the shape or peakedness characteristics.
一个随机变量可以用一个分布PDF(Probability Density Function)来描述。分布PDF可以用以下变量来描述:
均值mean
方差或标准差variance or standard deviation
斜度skewness
峭度kurtosis
如果mean, standard deviation, skewness, kurtosis已知,那么分布的相对位置,形状以及比例就可以计算出来。
均值mean的计算公式为:
\bar{x}=\frac{\sum_{i=1}^n{x_i}}{n}
其中x_i是第i个点的值。mean也被叫做一个分布关于0的一阶矩。
图:不同分布的mean值(红线代表均值)
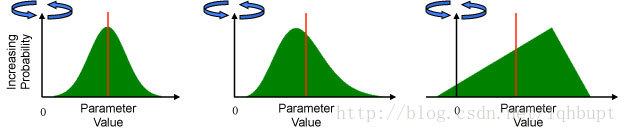
随机变量的展开情况可以用方差来描述,方差开根号得到标准差。方差相当于求分布关于均值的二阶矩。
方差variance的计算公式为:
\sigma^2=m_2=\frac{\sum_{i=1}^n(x_i-\bar{x})^2}{n}
随机变量分布对称性的描述成为斜度skewness,是{b_i}^0.5,是由分布关于均值的二阶矩和三阶矩计算得来。如果{b_i}^0.5<0,则分布是负斜度的,也就是tail在左边;如果{b_i}^0.5>0则分布是正斜度的,即tail在右边。斜度的计算方式如下:
\begin{multiline}
m_3=\frac{\sum_{i=1}^n(x_i-\bar{x})^3}{n}\\
\sqrt{b_1}=\frac{m_3}{(m_2)^{\frac32}}=\frac{m_3}{\sigma^3}
\end{multiline}
图:(a)正斜度的分布,长尾在右边;(b) 斜度为0; (c) 负斜度的分布,长尾在左边。红线为均值。

随机变量在均值附近的尖锐程度称为峭度kurtosis b_2,是由是由分布关于均值的四阶矩和二阶矩计算得来。如果b_2>>3,分布有一个尖峰;b_2=1.8分布是平坦;b=3,分布是高斯。峭度的计算方式如下:
\begin{multiline}
m_4=\frac{\sum_{i=1}^n(x_i-\bar{x})^4}{n}\\
b_2=\frac{m_4}{(m_2)^2}=\frac{m_4}{\sigma^4}
\end{multiline}
图:(a)峭度值b_2>>3;(b) 高斯分布,峭度b_2=3; (c) 平均分布,峭度为0。红线为均值。
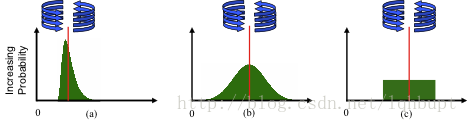
We know that the Mean gives us the central tendency of the data, the Standard Deviation explains the dispersion about the Mean, the Skewness represents the symmetry/asymmetry of the data, and the Kurtosis is related to the shape or peakedness characteristics.
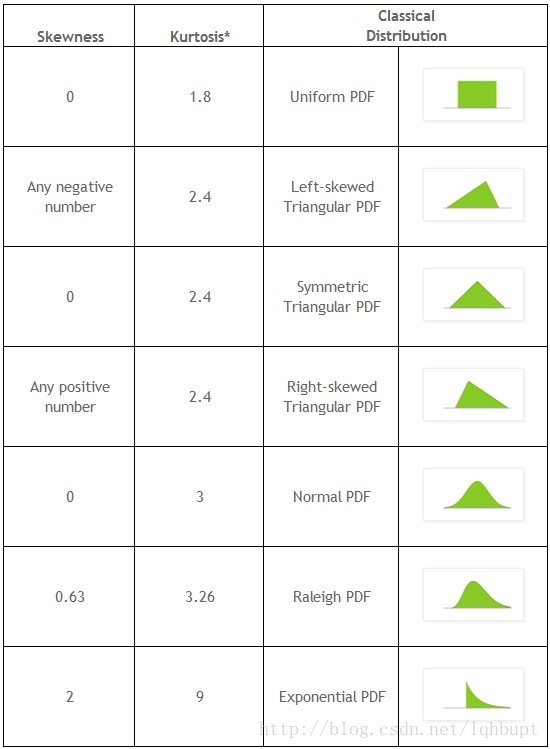
图:常见分布的斜度和峭度值
一个随机变量可以用一个分布PDF(Probability Density Function)来描述。分布PDF可以用以下变量来描述:
均值mean
方差或标准差variance or standard deviation
斜度skewness
峭度kurtosis
如果mean, standard deviation, skewness, kurtosis已知,那么分布的相对位置,形状以及比例就可以计算出来。
均值mean的计算公式为:
\bar{x}=\frac{\sum_{i=1}^n{x_i}}{n}
其中x_i是第i个点的值。mean也被叫做一个分布关于0的一阶矩。
图:不同分布的mean值(红线代表均值)

随机变量的展开情况可以用方差来描述,方差开根号得到标准差。方差相当于求分布关于均值的二阶矩。
方差variance的计算公式为:
\sigma^2=m_2=\frac{\sum_{i=1}^n(x_i-\bar{x})^2}{n}
图:分布(方差由小变大),红线为均值:
随机变量分布对称性的描述成为斜度skewness,是{b_i}^0.5,是由分布关于均值的二阶矩和三阶矩计算得来。如果{b_i}^0.5<0,则分布是负斜度的,也就是tail在左边;如果{b_i}^0.5>0则分布是正斜度的,即tail在右边。斜度的计算方式如下:
\begin{multiline}
m_3=\frac{\sum_{i=1}^n(x_i-\bar{x})^3}{n}\\
\sqrt{b_1}=\frac{m_3}{(m_2)^{\frac32}}=\frac{m_3}{\sigma^3}
\end{multiline}
图:(a)正斜度的分布,长尾在右边;(b) 斜度为0; (c) 负斜度的分布,长尾在左边。红线为均值。

随机变量在均值附近的尖锐程度称为峭度kurtosis b_2,是由是由分布关于均值的四阶矩和二阶矩计算得来。如果b_2>>3,分布有一个尖峰;b_2=1.8分布是平坦;b=3,分布是高斯。峭度的计算方式如下:
\begin{multiline}
m_4=\frac{\sum_{i=1}^n(x_i-\bar{x})^4}{n}\\
b_2=\frac{m_4}{(m_2)^2}=\frac{m_4}{\sigma^4}
\end{multiline}
图:(a)峭度值b_2>>3;(b) 高斯分布,峭度b_2=3; (c) 平均分布,峭度为0。红线为均值。


























 865
865

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








