1、基本概念
树(Tree)是n(n≥0)个结点的有限集。在任意一棵非空树中:(1)有且仅有一个特定的被称为根(Root)的结点;(2)当n>1时,其余结点可分为m(m>0)个互不相交的有限集T1,T2,…,Tm,其中每一个集合本身又是一棵树,并且称为根的子树(SubTree)。
度:结点拥有的子树数称为结点的度(Degree)。度为0的结点称为叶子(Leaf)或终端结点。度不为0的结点称为非终端结点或分支结点。树的度是树内各结点的度的最大值。
孩子及双亲:结点的子树的根称为该结点的孩子(Child),相应地,该结点称为孩子的双亲(Parent)。
层次“结点的层次(Level)是从根结点开始计算起,根为第一层,根的孩子为第二层,依次类推。树中结点的最大层次称为树的深度(Depth)或高度。
如果将树中结点的各子树看成从左至右是有次序的(即不能互换),则称该树为有序树,否则称为无序树。
2、二叉树的基本性质:
二叉树(Binary Tree)的特点是每个结点至多具有两棵子树(即在二叉树中不存在度大于2的结点),并且子树之间有左右之分。
二叉树的性质:
(1)、在二叉树的第i层上至多有2i-1个结点(i≥1)。
(2)、深度为k的二叉树至多有2k-1个结点(k≥1)。
(3)、对任何一棵二叉树,如果其叶子结点数为n0,度为2的结点数为n2,则n0=n2+1。
一棵深度为k且有2^k-1个结点的二叉树称为满二叉树。
可以对满二叉树的结点进行连续编号,约定编号从根结点起,自上而下,自左至右,则由此可引出完全二叉树的定义。深度为k且有n个结点的二叉树,当且仅当其每一个结点都与深度为k的满二叉树中编号从1到n的结点一一对应时,称之为完全二叉树。

(4)、具有n个结点的完全二叉树的深度为不大于log2n的最大整数加1。
(5)、如果对一棵有n个结点的完全二叉树的结点按层序编号(从第1层到最后一层,每层从左到右),则对任一结点i(1≤i≤n),有
a、如果i=1,则结点i是二叉树的根,无双亲;如果i>1,则其双亲是结点x(其中x是不大于i/2的最大整数)。
b、如果2i>n,则结点i无左孩子(结点i为叶子结点);否则其左孩子是结点2i。
c、如果2i+1>n,则结点i无右孩子;否则其右孩子是结点2i+1。
3、二叉查找树基本操作
查找:在二叉查找树中查找x的过程如下:
/**
* 二叉查找树的查找
* @param node
* @param x
*/
public TreeNode Find(TreeNode node,int x){
if(node == null)
return null;
if(x<node.val)
Find(node.left);
else if(x>node.val)
Find(node.right);
else if(x == node.val)
return node;
}
/**
* 查找最小值(递归实现)
* 一直查找左子树,最后一个节点即为最小值
* @param node
*/
public TreeNode FindMin(TreeNode node){
if(node == null)
return null;
else if(node.left == null)
return node;
else {
return FindMin(node.left);
}
}
/**
* 查找最大值(循环实现)
* 一直查找右子树
* @param node
*/
public TreeNode FindMax(TreeNode node){
if(node != null)
while(node.right != null)
node = node.right;
return node;
}二叉树查找树b插入操作x的过程如下:
/**
* 添加
* @param x
* @param root
* @return
*/
public TreeNode Insert(int x,TreeNode root){
if(root == null){ //找到要插入的位置,新建一个节点
TreeNode node = new TreeNode(x);
node.left = null;
node.right = null;
}
else if(x<root.val) //如果插入值小于当前值,则应插入左子树
root.left = Insert(x, root.left);
else if(x>root.val) //...
root.right = Insert(x, root.right);
return root;
}删除:
对于二叉查找树的删除操作(这里根据值删除,而非结点)分三种情况:








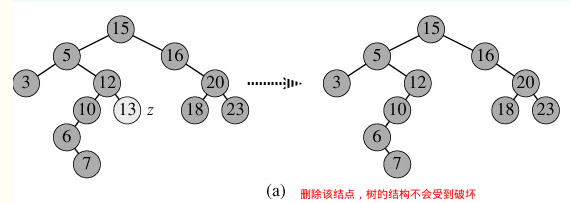
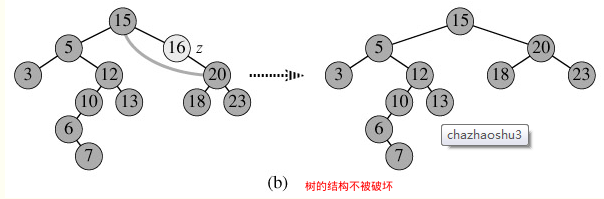
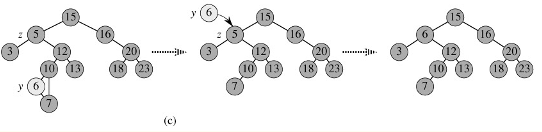














 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








