写在前面
本文主要分为三个部分。
第一部分介绍了二叉搜索树的基本性质。
第二部分全面详细地讲述了二叉搜索树的各种基本操作。包括WALK/遍历、SEARCH/查找、MINIMUM/最小关键字、MAXIMUM/最大关键字、SUCCESSOR/后继、PREDECESSOR/前驱、INSERT/插入、DELETE/删除等。主要参考《算法导论》（中文第3版）中有关二叉搜索树的相关介绍说明。
对于每一种基本操作，都至少分三个重点进行讲解。它们分别是基本操作过程及原理（包含伪代码及C++实现）、时间复杂度分析以及举例分析（配图）。力求让每位读者可以直观地理解。
第三部分则是完整的代码实现及实例分析。
本文断断续续写了几天，各部分的举例分析也十分明了，为了讲得更清楚一些，所有的配图都是自行制作的。请尊重劳动成果，供人供己查阅，如有错误之处，欢迎指正。
原创文章，转载请注明出处。http://blog.csdn.net/qq_21396469/article/details/78419609
一、二叉搜索树简介与基本性质
1、定义
二叉搜索树（BST）又称二叉查找树或二叉排序树。一棵二叉搜索树是以二叉树来组织的，可以使用一个链表数据结构来表示，其中每一个结点就是一个对象。一般地，除了key和卫星数据（文末附注1）之外，每个结点还包含属性lchild、rchild和parent，分别指向结点的左孩子、右孩子和双亲（父结点）。如果某个孩子结点或父结点不存在，则相应属性的值为空（NIL）。根结点是树中唯一父指针为NIL的结点，而叶子结点的孩子结点指针也为NIL。
2、基本性质
根据《算法导论》（中文第3版）的相关介绍，二叉搜索树中的关键字总是以满足二叉搜索树性质的方式来存储：
设x是二叉搜索树中的一个结点。如果y是x左子树中的一个结点，那么y.key≤x.key。如果y是x右子树中的一个结点，那么y.key≥x.key。
在二叉搜索树中：
① 若任意结点的左子树不空，则左子树上所有结点的值均不大于它的根结点的值；
② 若任意结点的右子树不空，则右子树上所有结点的值均不小于它的根结点的值；
③ 任意结点的左、右子树也分别为二叉搜索树。
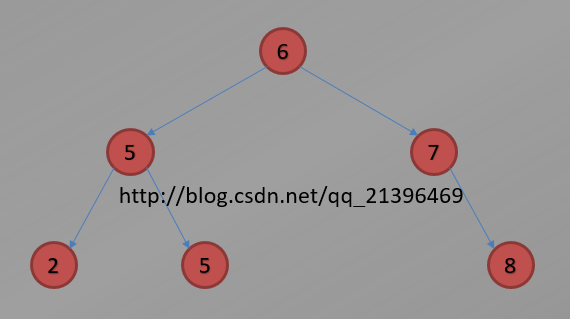
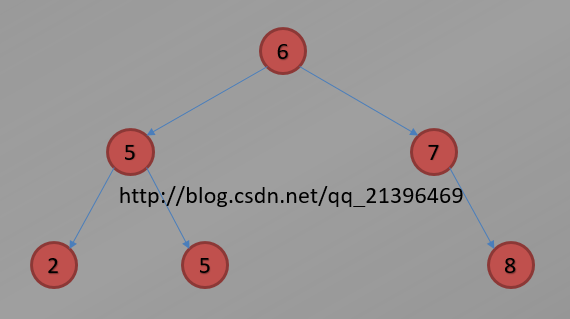
一棵典型的二叉搜索树如下：
二、二叉搜索树的基本操作与代码实现
1、二叉搜索树的结点
正如前面所说，每个二叉搜索树的结点，包含关键字key、左孩子指针lchild、右孩子指针rchild以及父结点指针parent。在C++实现中，我们定义一个结点类BSTNode来表示一个结点，并初始化结点的关键字等于0，左右孩子指针和父结点指针为NIL。/* 二叉搜索树节点 */
class BSTNode
{
private:
double key; // 关键字
BSTNode *lchild; // 左孩子
BSTNode *rchild; // 右孩子
BSTNode *parent; // 父节点
friend class BSTree;
public:
BSTNode(double k = 0.0, BSTNode *l = NULL, BSTNode *r = NULL, BSTNode *p = NULL) :key(k), lchild(l), rchild(r), parent(p){}
};
2、二叉搜索树的基本操作
对于一棵二叉搜索树来说，它支持许多动态集合操作，包括WALK（遍历）、SEARCH（查找）、MINIMUM（最小关键字）、MAXIMUM（最大关键字）、SUCCESSOR（后继）、PREDECESSOR（前驱）、INSERT（插入）、DELETE（删除）等。下面将依次讲解这些操作的具体过程及实现。
2.1 WALK（遍历）
2.1.1 中序遍历/INORDER-TREE-WALK
二叉搜索树的性质允许我们通过一个简单的递归算法来按序输出二叉搜索树中的所有关键字，这种算法称为中序遍历（inorder tree walk）算法。对于中序遍历来说，输出的子树根的关键字位于其左子树的关键字值和右子树的关键字值之间。其伪代码如下：
// 中序遍历
void inOrder_Tree_Walk(BSTNode *x)
{
if (x != NULL)
{
inOrder_Tree_Walk(x->lchild);
cout << x->key << " ";
inOrder_Tree_Walk(x->rchild);
}
}得益于二叉搜索树的性质，当使用中序遍历来访问一棵二叉搜索树上的所有结点时，最后得到的访问序列恰好是所有结点关键字的升序序列。
2.1.2 先序遍历/PREORDER-TREE-WALK
跟中序遍历类似，先序遍历（preorder tree walk）算法也是通过递归来实现的。区别在于先序遍历输出的子树根的关键字在其左右子树的关键字值之前。我们同样可以写出先序遍历的伪代码：
同样，根据上述伪代码，我们可以很容易地写出先序遍历二叉搜索树的实现。
// 先序遍历
void preOrder_Tree_Walk(BSTNode *x)
{
if (x != NULL)
{
cout << x->key << " ";
preOrder_Tree_Walk(x->lchild);
preOrder_Tree_Walk(x->rchild);
}
}
2.1.3 后序遍历/POSTORDER-TREE-WALK
跟中序遍历和先序遍历类似，后序遍历（postorder tree walk）算法也是通过递归来实现的。区别在于后序遍历输出的子树根的关键字在其左右子树的关键字值之后。同样地，我们可以写出后序遍历的伪代码：
根据上述伪代码，我们可以很容易地写出后序遍历二叉搜索树的实现。
// 后序遍历
void postOrder_Tree_Walk(BSTNode *x)
{
if (x != NULL)
{
postOrder_Tree_Walk(x->lchild);
postOrder_Tree_Walk(x->rchild);
cout << x->key << " ";
}
}
2.1.4 遍历的时间复杂度
遍历一棵有n个结点的二叉搜索树需要耗费θ(n)（文末附注2）的时间，因为初次调用之后，对于树中的每个节点这个过程恰好要自己调用两次：一次是它的左孩子，一次是它的右孩子。
根据《算法导论》（中文第3版）定理12.1：
如果x是一棵具有n个结点子树的根，那么调用INORDER-TREE-WALK(x)需要θ(n)的时间。
类似地，PREORDER-TREE-WALK(x)和POSTORDER-TREE-WALK(x)也只需要θ(n)的时间。
2.1.5 遍历访问序列举例
基于上述中序遍历、先序遍历、后序遍历的算法，对于下图典型的二叉搜索树来说，其三种遍历所得到的关键字访问序列分别为：
① 中序遍历：2、5、5（叶子）、6、7、8
② 先序遍历：6、5、2、5（叶子）、7、8
③ 后序遍历：2、5（叶子）、5、8、7、6
这里也验证了我们前面提到的一句话：使用中序遍历来访问一棵二叉搜索树上的所有结点时，最后得到的访问序列恰好是所有结点关键字的升序序列。
2.2 查找（SEARCH）
2.2.1 查找过程
在二叉搜索树中查找一个具有给定关键字key的结点，需要输入一个指向树根的指针x和一个关键字k，如果这个结点存在，则TREE-SEARCH返回一个指向关键字为k的结点的指针；否则返回NIL。
具体查找过程为：
① 从树根开始查找，并沿着这棵树中的一条简单路径向下进行；
② 若树为空树，则查找失败，返回NIL；
③ 对于遇到的每个结点x，若关键字k等于结点x的关键字，查找终止，返回指向结点x的指针；
④ 若关键字k小于结点x的关键字，则查找在x的左子树中继续（根据二叉搜索树的性质，k此时不可能在右子树中）；
⑤ 对称地，若关键字k大于结点x的关键字，则查找在x的右子树中继续（k此时不可能在左子树中）；
⑥ 若查找至叶子结点后仍未匹配到相等的关键字，则关键字为k的结点不存在，返回NIL。
2.2.2 递归查找/TREE-SEARCH
基于上述具体过程，可以写出二叉搜索树递归查找（TREE-SEARCH）的伪代码：
其相应的C++实现为：
/**
* 查找（递归实现）
* 输入：一个指向根节点的指针x，和待查找的关键字k
* 输出：指向关键字为k的节点的指针（若存在，否则输出NIL）
*/
BSTNode* tree_Search(BSTNode *x, double k)
{
if (x == NULL || k == x->key) // 如果找不着就返回NIL，找到了则返回对应节点的指针
return x;
if (k < x->key) // 关键字小于当前节点的关键字，查找就在左子树中继续
return tree_Search(x->lchild, k);
else // 关键字大于当前节点的关键字，查找就在右子树中继续
return tree_Search(x->rchild, k);
}
2.2.3 迭代实现/ITERATIVE-TREE-SEARCH
我们知道，递归调用和退出时需要频繁的压栈和出栈操作。若问题规模比较大，则会在递归调用时耗费不少时间。因此，为了进一步解决这个问题，可以考虑使用非递归的结构，节省递归导致的额外开销，从而提升算法的时间效率。
我们可以采用while循环来展开递归，用一种迭代方式重写上述过程。对于大多数计算机，迭代版本的效率要高得多。
二叉搜索树的迭代查找（ITERATIVE-TREE-SEARCH）的伪代码为：
相应的C++实现为：
/**
* 查找（迭代实现）
* 输入：一个指向根节点的指针x，和待查找的关键字k
* 输出：指向关键字为k的节点的指针（若存在，否则输出NIL）
*/
BSTNode* iterative_Tree_Search(BSTNode *x, double k)
{
while (x != NULL && k != x->key)
{
if (k < x->key) // 关键字小于当前节点的关键字，查找就在左子树中继续
x = x->lchild;
else // 关键字大于当前节点的关键字，查找就在右子树中继续
x = x->rchild;
}
return x; // 如果找不着就返回NIL，找到了则返回对应节点的指针
}
2.2.4 查找的时间复杂度
对于二叉搜索树的查找，从树根开始递归/迭代期间遇到的结点形成了一条向下的简单路径。在最坏情况下，关键字k从树根开始直至叶子结点都没有匹配或者在叶子结点才匹配到，这样比较的结点个数等于树的高度h。
因此，二叉搜索树的查找TREE-SEARCH/ITERATIVE-TREE-SEARCH的时间复杂度为O(h)，其中h为二叉搜索树的高度。
2.2.5 查找举例
对于以下的二叉搜索树，查找关键字为13的结点。
查找首先从根结点开始，13<15，查找左子树；13>6，查找右子树；13>7，继续查找右子树；13==13，关键字相等，查找结束。成功找到了关键字为13的结点，并返回指向它的指针。并且，查找过程中遇到的结点形成了一条向下的简单路径。
2.3 最小关键字（MINIMUM）
2.3.1 最小关键字查询过程
根据二叉搜索树的性质，对于非叶子结点来说，其左子树的关键字总是不大于该结点的关键字。从一棵子树的树根开始，沿着lchild指针直到遇到一个NIL，我们总能在一棵二叉搜索树中找到一个指针，这个指针指向该子树中的最小元素。
二叉搜索树中查询最小关键字（MINIMUM）的伪代码如下：
根据上述伪代码，可以直接写出其C++实现。
// 查找以节点x为根的子树的最小关键字并返回其节点指针
BSTNode* tree_Minimum(BSTNode *x)
{
while (x->lchild != NULL)
{
x = x->lchild; // 从树根x沿着lchild指针一直往下找，直到遇到一个NIL
}
return x;
}二叉搜索树性质保证了TREE-MINIMUM是正确的。如果结点x没有左子树，那么由于x右子树中的每个关键字都至少大于或等于x.key，则以x为根的子树中的最小关键字是x.key。如果结点x有左子树，那么由于其右子树中没有关键字小于x.key，且在左子树中的每个关键字不大于x.key，则以x为根的子树中的最小关键字一定在以x.lchild为根的子树中。
2.3.2 最小关键字的时间复杂度
在一棵二叉搜索树上查询最小关键字时，从树根开始，沿着lchild指针直到遇到一个NIL，途中遇到的结点形成了一条向下的简单路径。最小关键字在二叉搜索树最左结点找到（不一定是最左边的叶子结点）。
因此，查询二叉搜索树的最小关键字的时间复杂度为O(h)，其中h为二叉搜索树的高度。
2.3.3 最小关键字举例
如下图，查询一棵二叉搜索树的最小关键字。
首先从树根结点15开始，沿着lchild指针一路向下，路径为15->6->3->2。因此，该二叉搜索树的最小关键字为2。
2.4 最大关键字（MAXIMUM）
2.4.1 最大关键字查询过程
最大关键字的查询过程与最小关键字的十分类似。根据二叉搜索树的性质，对于非叶子结点来说，其右子树的关键字总是不小于该结点的关键字。从一棵子树的树根开始，沿着rchild指针直到遇到一个NIL，我们总能在一棵二叉搜索树中找到一个指针，这个指针指向该子树中的最大元素。
二叉搜索树中查询最大关键字（MAXIMUM）的伪代码如下：
根据上述伪代码，可以直接写出其C++实现。
// 查找以节点x为根的子树的最大关键字并返回其节点指针
BSTNode* tree_Maximum(BSTNode *x)
{
while (x->rchild != NULL)
{
x = x->rchild; // 从树根x沿着rchild指针一直往下找，直到遇到一个NIL
}
return x;
}二叉搜索树性质保证了TREE-MAXIMUM是正确的。如果结点x没有右子树，那么由于x左子树中的每个关键字都至多小于或等于x.key，则以x为根的子树中的最大关键字是x.key。如果结点x有右子树，那么由于其左子树中没有关键字大于x.key，且在右子树中的每个关键字不小于x.key，则以x为根的子树中的最大关键字一定在以x.rchild为根的子树中。
2.4.2 最大关键字的时间复杂度
在一棵二叉搜索树上查询最小关键字时，从树根开始，沿着rchild指针直到遇到一个NIL，途中遇到的结点形成了一条向下的简单路径。最大关键字在二叉搜索树最右结点找到（不一定是最右边的叶子结点）。
因此，查询二叉搜索树的最大关键字的时间复杂度为O(h)，其中h为二叉搜索树的高度。
2.4.3 最大关键字举例
如下图，查询一棵二叉搜索树的最大关键字。
首先从树根结点15开始，沿着rchild指针一路向下，路径为15->18->20。因此，该二叉搜索树的最大关键字为20。
2.5 SUCCESSOR（后继）
2.5.1 查询某个结点的后继的过程
给定一棵二叉搜索树中的一个结点，有时候需要按中序遍历的次序查找它的后继。一棵二叉搜索树的结构允许我们通过没有任何关键字的比较来确定一个结点的后继。如果后继存在，则返回指向结点x的后继的指针。倘若结点x的关键字是这棵树的最大关键字，则说明它没有后继了，返回NIL。
求后继的过程可以分以下两种情况讨论：
① 如果结点x的右子树非空，那么x的后继恰是x右子树中的最左结点（右子树中的最小关键字）；
② 如果结点x的右子树为空，则有以下两种可能：
a. 结点x是其父结点的左孩子，则结点x的后继结点为它的父结点；
b. 结点x是其父结点的右孩子，则结点x的后继结点为x的最底层祖先，同时满足“这个最底层祖先的左孩子也是结点x的祖先”的条件。（可以结合2.5.3的例子进行理解）
在二叉搜索树中查询某个结点后继（SUCCESSOR）的伪代码如下：
根据上述伪代码，我们可以写出它的C++实现。
// 查找节点x的后继节点并返回
BSTNode* tree_Successor(BSTNode *x)
{
BSTNode *y = NULL;
if (x->rchild != NULL) // 若节点x的右孩子不为空，则x的后继节点就是其右子树中的最小关键字节点
return tree_Minimum(x->rchild);
// 若节点x的右孩子为空，则有以下两种情况
// a.结点x是其父结点的左孩子，则结点x的后继结点为它的父结点；
// b.结点x是其父结点的右孩子，则结点x的后继结点为x的最底层祖先，同时满足“这个最底层祖先的左孩子也是结点x的祖先”的条件。
y = x->parent; // 若节点x的右孩子为空，先令y为x的父节点
while (y != NULL && x == y->rchild) // 从x开始沿树而上直到遇到这样一个节点x，这个节点x是它的双亲y的左孩子，此时双亲即为后继节点
{
x = y;
y = y->parent;
}
return y;
}
2.5.2 查询结点后继的时间复杂度
当给定一棵二叉搜索树的某个结点x，要求该结点的后继结点时，这个过程或者遵从一条简单路径沿树向下（结点x的右子树非空时的情况，只需找右子树中的最小关键字即可）；或者遵从简单路径沿树向上（结点x的右子树为空时的情况，只需沿树向上查找符合条件的最底层祖先即可）。
因此，不管是哪种情况，这个过程最坏情况下都是一条从根到叶子结点或者从叶子结点到根的完整路径。所以，当给定一棵二叉搜索树的某个结点，求该结点的后继结点的时间复杂度为O(h)，其中h为二叉搜索树的高度。
2.5.3 查询结点后继举例
如下图，为一棵二叉搜索树。前面我们说过，求后继的过程可以分为以下两种情况：
① 如果结点x的右子树非空，那么x的后继恰是x右子树中的最左结点（右子树中的最小关键字）；
② 如果结点x的右子树为空，则有以下两种可能：
a. 结点x是其父结点的左孩子，则结点x的后继结点为它的父结点；
b. 结点x是其父结点的右孩子，则结点x的后继结点为x的最底层祖先，同时满足“这个最底层祖先的左孩子也是结点x的祖先”的条件。
对于情况①，假设我们要求结点15的后继。因为结点15的右子树非空，所以15的后继就是它的右子树中的最小关键字，即为17。
对于情况②a，假设我们要求结点9的后继。因为结点9的右子树为空，且结点9是其父结点13的左孩子，所以9的后继就是它的父结点，即为13。
对于情况②b，假设我们要求结点13的后继。因为结点13的右子树为空，且结点13是其父结点7的右孩子。此时我们要找的后继是13的最底层祖先，而且这个最底层祖先的左孩子也是结点13的祖先之一。
我们可以这样看，首先结点13的祖先有7、6、15,；按理说最底层结点应该是7。但是我们需要注意，这个最底层是有前提条件的。前提条件就是这个祖先要有左孩子，并且这个左孩子也是结点13的祖先之一。
在祖先7、6、15中，有左孩子的有6和15，但是结点6的左孩子3并不是结点13的祖先之一；结点15的左孩子6正是结点13的另一个祖先。因此，符合前提条件的最底层祖先为15。所以13的后继就是15。
2.6 PREDECESSOR（前驱）
2.6.1 查询某个结点的前驱的过程
给定一棵二叉搜索树中的一个结点查找它的前驱的情况跟求后继的情况是对称的。一棵二叉搜索树的结构也允许我们通过没有任何关键字的比较来确定一个结点的前驱。如果前驱存在，则返回指向结点x的前驱的指针。倘若结点x的关键字是这棵树的最小关键字，则说明它没有前驱了，返回NIL。
求前驱的过程同样可以分以下两种情况讨论：
① 如果结点x的左子树非空，那么x的前驱恰是x左子树中的最右结点（左子树中的最大关键字）；
② 如果结点x的左子树为空，则有以下两种可能：
a. 结点x是其父结点的右孩子，则结点x的前驱结点为它的父结点；
b. 结点x是其父结点的左孩子，则结点x的前驱结点为x的最底层祖先，同时满足“这个最底层祖先的右孩子也是结点x的祖先”的条件。（可以结合2.6.3的例子进行理解）
在二叉搜索树中查询某个结点前驱（PREDECESSOR）的伪代码如下：
根据上述伪代码，我们可以写出它的C++实现。
// 查找节点x的前驱节点并返回
BSTNode* tree_Predecessor(BSTNode *x)
{
BSTNode *y = NULL;
if (x->lchild != NULL) // 若节点的左孩子不为空，则x的前驱节点就是其左子树中的最大关键字节点
return tree_Maximum(x->lchild);
// 若节点x的左孩子为空，则有以下两种情况
// a.结点x是其父结点的右孩子，则结点x的前驱结点为它的父结点；
// b.结点x是其父结点的左孩子，则结点x的前驱结点为x的最底层祖先，同时满足“这个最底层祖先的右孩子也是结点x的祖先”的条件。
y = x->parent; // 若节点的左孩子为空，先令y为x的父节点
while (y != NULL && x == y->lchild) // 从x开始沿树而上直到遇到这样一个节点x，这个节点x是它的双亲y的右孩子，此时双亲即为前驱节点
{
x = y;
y = y->parent;
}
return y;
}
2.6.2 查询结点前驱的时间复杂度
当给定一棵二叉搜索树的某个结点x，要求该结点的前驱结点时，这个过程或者遵从一条简单路径沿树向下（结点x的左子树非空时的情况，只需找左子树中的最大关键字即可）；或者遵从简单路径沿树向上（结点x的左子树为空时的情况，只需沿树向上查找符合条件的最底层祖先即可）。
因此，不管是哪种情况，这个过程最坏情况下都是一条从根到叶子结点或者从叶子结点到根的完整路径。所以，当给定一棵二叉搜索树的某个结点，求该结点的前驱结点的时间复杂度为O(h)，其中h为二叉搜索树的高度。
2.6.3 查询结点前驱举例
如下图，为一棵二叉搜索树。前面我们说过，求前驱的过程可以分为以下两种情况：
① 如果结点x的左子树非空，那么x的前驱恰是x左子树中的最右结点（左子树中的最大关键字）；
② 如果结点x的左子树为空，则有以下两种可能：
a. 结点x是其父结点的右孩子，则结点x的前驱结点为它的父结点；
b. 结点x是其父结点的左孩子，则结点x的前驱结点为x的最底层祖先，同时满足“这个最底层祖先的右孩子也是结点x的祖先”的条件。
对于情况①，假设我们要求结点15的前驱。因为结点15的左子树非空，所以15的前驱就是它的左子树中的最大关键字，即为13。
对于情况②a，假设我们要求结点7的前驱。因为结点7的左子树为空，且结点7是其父结点6的右孩子，所以7的前驱就是它的父结点，即为6。
对于情况②b，假设我们要求结点17的前驱。因为结点17的左子树为空，且结点17是其父结点18的左孩子。此时我们要找的前驱是17的最底层祖先，而且这个最底层祖先的右孩子也是结点17的祖先之一。
我们可以这样看，首先结点17的祖先有18、15,；按理说最底层结点应该是18。但是我们需要注意，这个最底层是有前提条件的。前提条件就是这个祖先要有右孩子，并且这个右孩子也是结点17的祖先之一。
在祖先18、15中，两个结点都有右孩子，但是结点18的右孩子20并不是结点17的祖先之一；结点15的右孩子18正是结点17的另一个祖先。因此，符合前提条件的最底层祖先为15。所以17的前驱就是15。
到这里，我们可以结合最小关键字、最大关键字、后继、前驱的查找过程来证明一下《算法导论》（中文第3版）课后题12.2-5：如果有一棵二叉搜索树中的一个结点有两个孩子，那么它的后继没有左孩子，它的前驱没有右孩子。
证明：
倘若一棵二叉搜索树的结点有两个孩子。则：
当求该结点x的后继时，因为它的右孩子非空，符合求后继的情况①，结点x的后继y1就是它右子树中的最小关键字。假设该最小关键字y1有左孩子z1，则根据二叉搜索树的性质，z1.key≤y1.key，这与y1是最小关键字相矛盾。所以后继y1没有左孩子。
另外，当求该结点x的前驱时，因为它的左孩子非空，符合求前驱的情况①，结点x的前驱y2就是它的左子树中的最大关键字。假设该最大关键字y2有右孩子z2，则根据二叉搜索树的性质，z2.key≥y2.key，这与y2是最大关键字相矛盾。所以前驱y2没有右孩子。
因此，如果有一棵二叉搜索树中的一个结点有两个孩子，那么它的后继没有左孩子，它的前驱没有右孩子。
证毕。
2.7 INSERT（插入）
2.7.1 插入过程
插入操作会引起由二叉搜索树表示的动态集合的变化。我们需要修改数据结构来反映这个变化，但要保证修改后二叉搜索树的性质不被破坏。
要将一个新值v插入到一棵二叉搜索树T中，需要新建一个结点z，并且初始化z.key = v，z.lchild= NIL，z.rchild = NIL。现在问题转化为将结点z插入到二叉搜索树T中的合适位置，并且保持二叉搜索树的性质不变。
插入的过程首先从树根开始遍历，沿树向下移动。指针x记录了一条向下的简单路径，并查找要替换的输入项z的NIL。同时，保持遍历指针y指向x的双亲。两个指针沿树向下移动时，通过比较当前结点x的关键字与待插入结点z的关键字大小，来决定向左或向右移动。直到x指向NIL时，这个NIL占据的位置就是输入项z要放置的位置。前面我们提到在x移动过程中还需要保持y指向x的父结点，原因是当我们找到可插入的NIL位置时，我们需要知道z属于哪个结点。
在二叉搜索树中插入（INSERT）新结点的相应伪代码如下：
根据上述伪代码，其相应的C++实现为：
// 将节点z插入到以T为根节点的二叉搜索树中
void tree_Insert(BSTNode *&T, BSTNode *z)
{
BSTNode *x = T;
BSTNode *y = NULL;
while (x != NULL) // 使得指针沿树向下移动，向左或向右移动取决于z->key和x->key的比较
{
y = x;
if (z->key < x->key) // 关键字小于当前节点的关键字，向左子树移动
x = x->lchild;
else // 关键字大于或等于当前节点的关键字，向右子树移动
x = x->rchild;
}
z->parent = y; // 节点z的父节点指针指向遍历到的节点y
if (y == NULL) // 若y为NIL，说明原树为空
T = z; // 将节点z作为根节点插入
else if (z->key < y->key) // 若y不为NIL，且z的关键字小于y的关键字
y->lchild = z; // 将y的左孩子指针指向节点z
else // 若y不为NIL，且z的关键字大于等于y的关键字
y->rchild = z; // 将y的右孩子指针指向节点z
}值得注意的是，在插入新结点后，新结点总是作为一个新叶子结点而存在的。这是二叉搜索树的另一个重要性质。
2.7.2 插入的时间复杂度
在一棵二叉搜索树中插入新结点，跟TREE-SEARCH、MINIMUM等操作类似，都是从树根开始，遇到的结点形成了一条向下的简单路径。在插入过程中，需要从树根开始向下移动，一直比较到叶子结点。
所以，当给定一棵二叉搜索树，向其中插入新结点的时间复杂度为O(h)，其中h为二叉搜索树的高度。
2.7.3 插入新结点举例
如下图，是一棵二叉搜索树，现有新结点13要插入到这棵树中。
首先从树根开始，关键字13>12，因此指针向右子树移动。而13<18，故指针向左子树移动。13<15，指针继续向左子树移动。但因为此刻指针指向的是NIL了，因此这个位置就是新结点13所要插入的位置。修改相应的左右孩子指针及父结点指针，同时父结点也修改相应的孩子指针即可。整条搜索至完成插入的路径为12->18->15->13。
2.8 DELETE（删除）
2.8.1 删除过程
跟插入操作一样，删除操作也会引起二叉搜索树表示的动态集合的变化。我们也需要修改数据结构来反映这个变化。但是仍然需要保证删除后二叉搜索树的性质不变。但是，相对于插入操作，删除操作会更加复杂一些。
从一棵二叉搜索树中删除某个特定结点z可以分为以下三种情况，其中前两种情况较为简单，最后一种情况则复杂一点。
① 如果z没有孩子结点，那么只是简单地将它删除，并修改它的父结点，用NIL作为孩子来替换z；
② 如果z只有一个孩子，那么将这个孩子提升到树中z的位置上，并修改z的父结点，用z的孩子来替换z；
z只有一个孩子，且为右孩子，用z的右子树替换z：
z只有一个孩子，且为左孩子，用z的左子树替换z：
③ 如果z有两个孩子，那么找z的后继y，并让y占据树中z的位置。z的原来右子树部分成为y的新的右子树，z的原来左子树部分成为y新的左子树。这里要注意，z的后继y一定在z的右子树中，并且没有左孩子（详情见上文2.7前的证明）。利用z的后继y替换z，又细分为以下两种情况：
a. 如果y是z的右孩子，那么直接用y替换z，并保留y的右子树（y没有左子树）；
b. 如果y不是z的右孩子，那么先用y的右孩子替换y（y没有左孩子），然后再用y替换z。
删除操作也需要从树根开始，搜索待删除的关键字的结点是否在树中。若不存在，则删除失败；若存在则根据上述的三种情况执行删除操作。
为了在二叉搜索树中移动子树，我们首先定义一个子过程TRANSPLANT，它是用一棵以v为根的子树来替换一棵以u为根的子树，将结点u的父结点变为结点v的父结点，同时修改原u的父结点的孩子指针，使其指向v。简单来说，这个子过程的主要工作就是修改v的父结点指针，同时修改原u父结点的孩子指针，这样以v为根的子树就替换上去了。
该TRANSPLANT的伪代码如下：
结合上面的TRANSPLANT子过程，我们可以进一步写出从二叉搜索树中删除（DELETE）结点的伪代码如下：
根据上述伪代码，可以写出子过程TRANSPLANT以及DELETE操作的C++实现为：
// 用一棵以v为根的子树来替换一棵以u为根的子树，节点u的双亲变成节点v的双亲，并且v成为u的双亲的相应孩子
void transplant(BSTNode *&T, BSTNode *u, BSTNode *v)
{
if (u->parent == NULL) // 节点u为根节点时
T = v; // 节点v直接替换u作为根节点
else if (u == u->parent->lchild) // 节点u是其父节点的左孩子
u->parent->lchild = v; // 父节点的左孩子指向节点v
else // 节点u是其父节点的右孩子
u->parent->rchild = v; // 父节点的右孩子指向节点v
if (v != NULL)
v->parent = u->parent; // 更新节点v的父节点指针
} // 将节点z从以T为根节点的二叉搜索树中删除
BSTNode* tree_Delete(BSTNode *&T, BSTNode *z)
{
BSTNode *y = NULL;
if (z->lchild == NULL) // 若z的左孩子为NIL，直接用z的右孩子替换z
transplant(T, z, z->rchild);
else if (z->rchild == NULL) // 若z的右孩子为NIL，直接用z的左孩子替换z
transplant(T, z, z->lchild);
else // 若z有两个孩子
{
// 先让y为z的后继，也即z的右子树中的最小关键字
// y肯定没有左孩子，否则最小关键字就是那个左孩子而不是y了
y = tree_Minimum(z->rchild);
if (y->parent != z) // 若y不是z的右孩子
{
transplant(T, y, y->rchild); // 先用y的右孩子替换y
y->rchild = z->rchild; // y的右子树指针指向原来z的右子树指针
y->rchild->parent = y; // 原来z的右子树（现为y的右子树）的父节点指针更新为y
}
transplant(T, z, y); // 然后再用y替换z
y->lchild = z->lchild; // y的左子树指针指向原来z的左子树指针
y->lchild->parent = y; // 原来z的左子树（现为y的左子树）的父节点指针更新为y
}
return z;
}2.8.2 删除的时间复杂度
在一棵二叉搜索树中删除结点，我们可以看到DELETE操作实现的每一步，都只需要耗费常数时间。子过程TRANSPLANT的每一步实现也只需要常数时间。时间效率主要取决于在二叉搜索树中查找要删除的结点关键字是否存在。因此，删除操作的时间复杂度是由查找操作的时间复杂度来决定的。
由于查找（SEARCH）的时间复杂度为O(h)，因此，当给定一棵二叉搜索树，删除结点的时间复杂度为O(h)，其中h为二叉搜索树的高度。
2.8.3 删除结点举例
其实这部分已在2.8.1描述删除过程时针对不同情况均已举出了相关例子。详情请见2.8.1的文字描述及配图示例。
三、完整代码及测试实例
1、测试实例：利用完整代码，假如我们想构建下图这样一棵二叉搜索树。由于程序中使用插入操作来完成一棵二叉搜索树的构建，因此，我们在输入关键字序列时要注意一点：就是每棵子树的根结点关键字要先于它的孩子结点的关键字输入。
举个例子来说，下图的二叉搜索树，输入序列为：15 6 18 3 7 17 20 2 4 13 9 或者 15 6 18 3 2 47 13 9 17 20 等都是可以的，因为这些序列都确保了子树的根结点关键字先于其孩子结点关键字输入。但是，类似于：15 6 2 4 3 7 13 9 18 17 20 的序列则是不合法的，无法构建出下图的二叉搜索树，原因是子树根3后于其孩子结点2 4输入了。
接下来我们开始进行测试，首先输入结点/关键字个数。就上图而言，结点/关键字个数为11个。接下来按照合法序列输入关键字序列：15 6 18 3 7 17 20 2 413 9。
可以看到当构建完二叉搜索树后，输出了先序、中序、后序遍历的访问序列，我们可以自行根据上图的二叉搜索树进行验证。同时，因为先序+中序（或者中序+后序）可以唯一确定一棵二叉树，所以此处可以验证我们构建的二叉搜索树是否就是上图的二叉搜索树。
接下来我们查找一下结点。比如我们查找结点13，由于上图树中存在结点13，因此查找成功。当我们查找不存在的结点时，比如结点14，就会查找失败。
最后我们来测试一下删除的操作。删除根节点15，因为结点15有两个孩子结点，并且其后继17不是它的右孩子，属于删除情况中最复杂的一种情况。
在这种情况下，删除操作应该首先用后继17的右孩子替换17。此例中右孩子为NIL，也就是用NIL替换17。然后用后继17来替换结点15，原15的左右子树变为17的左右子树了。
删除操作完成后，我们可以继续输出先序+中序（或者中序+后序）的访问序列。因为先序+中序（或者中序+后序）可以唯一确定一棵二叉树，所以此处可以验证删除结点15后的二叉搜索树是否跟我们预想的一致。
删除根结点15后的新二叉搜索树如下：
至此，简单的测试实例已经测试完毕。下面将贴出完整代码。
2、完整代码如下：
#include <iostream>
using namespace std;
/* 二叉搜索树节点 */
class BSTNode
{
private:
double key; // 关键字
BSTNode *lchild; // 左孩子
BSTNode *rchild; // 右孩子
BSTNode *parent; // 父节点
friend class BSTree;
public:
BSTNode(double k = 0.0, BSTNode *l = NULL, BSTNode *r = NULL, BSTNode *p = NULL) :key(k), lchild(l), rchild(r), parent(p){}
};
/* 二叉搜索树 */
class BSTree
{
private:
BSTNode *root; // 根节点
/* 以下是内部接口 */
// 先序遍历
void preOrder_Tree_Walk(BSTNode *x)
{
if (x != NULL)
{
cout << x->key << " ";
preOrder_Tree_Walk(x->lchild);
preOrder_Tree_Walk(x->rchild);
}
}
// 中序遍历
void inOrder_Tree_Walk(BSTNode *x)
{
if (x != NULL)
{
inOrder_Tree_Walk(x->lchild);
cout << x->key << " ";
inOrder_Tree_Walk(x->rchild);
}
}
// 后序遍历
void postOrder_Tree_Walk(BSTNode *x)
{
if (x != NULL)
{
postOrder_Tree_Walk(x->lchild);
postOrder_Tree_Walk(x->rchild);
cout << x->key << " ";
}
}
/**
* 查找（递归实现）
* 输入：一个指向根节点的指针x，和待查找的关键字k
* 输出：指向关键字为k的节点的指针（若存在，否则输出NIL）
*/
BSTNode* tree_Search(BSTNode *x, double k)
{
if (x == NULL || k == x->key) // 如果找不着就返回NIL，找到了则返回对应节点的指针
return x;
if (k < x->key) // 关键字小于当前节点的关键字，查找就在左子树中继续
return tree_Search(x->lchild, k);
else // 关键字大于当前节点的关键字，查找就在右子树中继续
return tree_Search(x->rchild, k);
}
/**
* 查找（迭代实现）
* 输入：一个指向根节点的指针x，和待查找的关键字k
* 输出：指向关键字为k的节点的指针（若存在，否则输出NIL）
*/
BSTNode* iterative_Tree_Search(BSTNode *x, double k)
{
while (x != NULL && k != x->key)
{
if (k < x->key) // 关键字小于当前节点的关键字，查找就在左子树中继续
x = x->lchild;
else // 关键字大于当前节点的关键字，查找就在右子树中继续
x = x->rchild;
}
return x; // 如果找不着就返回NIL，找到了则返回对应节点的指针
}
// 查找以节点x为根的子树的最小关键字并返回其节点指针
BSTNode* tree_Minimum(BSTNode *x)
{
while (x->lchild != NULL)
{
x = x->lchild; // 从树根x沿着lchild指针一直往下找，直到遇到一个NIL
}
return x;
}
// 查找以节点x为根的子树的最大关键字并返回其节点指针
BSTNode* tree_Maximum(BSTNode *x)
{
while (x->rchild != NULL)
{
x = x->rchild; // 从树根x沿着rchild指针一直往下找，直到遇到一个NIL
}
return x;
}
// 查找节点x的后继节点并返回
BSTNode* tree_Successor(BSTNode *x)
{
BSTNode *y = NULL;
if (x->rchild != NULL) // 若节点x的右孩子不为空，则x的后继节点就是其右子树中的最小关键字节点
return tree_Minimum(x->rchild);
// 若节点x的右孩子为空，则有以下两种情况
// a.结点x是其父结点的左孩子，则结点x的后继结点为它的父结点；
// b.结点x是其父结点的右孩子，则结点x的后继结点为x的最底层祖先，同时满足“这个最底层祖先的左孩子也是结点x的祖先”的条件。
y = x->parent; // 若节点x的右孩子为空，先令y为x的父节点
while (y != NULL && x == y->rchild) // 从x开始沿树而上直到遇到这样一个节点x，这个节点x是它的双亲y的左孩子，此时双亲即为后继节点
{
x = y;
y = y->parent;
}
return y;
}
// 查找节点x的前驱节点并返回
BSTNode* tree_Predecessor(BSTNode *x)
{
BSTNode *y = NULL;
if (x->lchild != NULL) // 若节点的左孩子不为空，则x的前驱节点就是其左子树中的最大关键字节点
return tree_Maximum(x->lchild);
// 若节点x的左孩子为空，则有以下两种情况
// a.结点x是其父结点的右孩子，则结点x的前驱结点为它的父结点；
// b.结点x是其父结点的左孩子，则结点x的前驱结点为x的最底层祖先，同时满足“这个最底层祖先的右孩子也是结点x的祖先”的条件。
y = x->parent; // 若节点的左孩子为空，先令y为x的父节点
while (y != NULL && x == y->lchild) // 从x开始沿树而上直到遇到这样一个节点x，这个节点x是它的双亲y的右孩子，此时双亲即为前驱节点
{
x = y;
y = y->parent;
}
return y;
}
// 将节点z插入到以T为根节点的二叉搜索树中
void tree_Insert(BSTNode *&T, BSTNode *z)
{
BSTNode *x = T;
BSTNode *y = NULL;
while (x != NULL) // 使得指针沿树向下移动，向左或向右移动取决于z->key和x->key的比较
{
y = x;
if (z->key < x->key) // 关键字小于当前节点的关键字，向左子树移动
x = x->lchild;
else // 关键字大于或等于当前节点的关键字，向右子树移动
x = x->rchild;
}
z->parent = y; // 节点z的父节点指针指向遍历到的节点y
if (y == NULL) // 若y为NIL，说明原树为空
T = z; // 将节点z作为根节点插入
else if (z->key < y->key) // 若y不为NIL，且z的关键字小于y的关键字
y->lchild = z; // 将y的左孩子指针指向节点z
else // 若y不为NIL，且z的关键字大于等于y的关键字
y->rchild = z; // 将y的右孩子指针指向节点z
}
// 用一棵以v为根的子树来替换一棵以u为根的子树，节点u的双亲变成节点v的双亲，并且v成为u的双亲的相应孩子
void transplant(BSTNode *&T, BSTNode *u, BSTNode *v)
{
if (u->parent == NULL) // 节点u为根节点时
T = v; // 节点v直接替换u作为根节点
else if (u == u->parent->lchild) // 节点u是其父节点的左孩子
u->parent->lchild = v; // 父节点的左孩子指向节点v
else // 节点u是其父节点的右孩子
u->parent->rchild = v; // 父节点的右孩子指向节点v
if (v != NULL)
v->parent = u->parent; // 更新节点v的父节点指针
}
// 将节点z从以T为根节点的二叉搜索树中删除
BSTNode* tree_Delete(BSTNode *&T, BSTNode *z)
{
BSTNode *y = NULL;
if (z->lchild == NULL) // 若z的左孩子为NIL，直接用z的右孩子替换z
transplant(T, z, z->rchild);
else if (z->rchild == NULL) // 若z的右孩子为NIL，直接用z的左孩子替换z
transplant(T, z, z->lchild);
else // 若z有两个孩子
{
// 先让y为z的后继，也即z的右子树中的最小关键字
// y肯定没有左孩子，否则最小关键字就是那个左孩子而不是y了
y = tree_Minimum(z->rchild);
if (y->parent != z) // 若y不是z的右孩子
{
transplant(T, y, y->rchild); // 先用y的右孩子替换y
y->rchild = z->rchild; // y的右子树指针指向原来z的右子树指针
y->rchild->parent = y; // 原来z的右子树（现为y的右子树）的父节点指针更新为y
}
transplant(T, z, y); // 然后再用y替换z
y->lchild = z->lchild; // y的左子树指针指向原来z的左子树指针
y->lchild->parent = y; // 原来z的左子树（现为y的左子树）的父节点指针更新为y
}
return z;
}
// 销毁二叉搜索树
void tree_Destory(BSTNode *&T)
{
if (T == NULL)
return;
if (T->lchild != NULL)
return tree_Destory(T->lchild);
if (T->rchild != NULL)
return tree_Destory(T->rchild);
delete T;
T = NULL;
}
public:
BSTree() :root(NULL){}
/* 以下是外部接口 */
// 先序遍历
void PreOrder_Tree_Walk()
{
preOrder_Tree_Walk(root); // 传入根节点
cout << endl;
}
// 中序遍历
void InOrder_Tree_Walk()
{
inOrder_Tree_Walk(root); // 传入根节点
cout << endl;
}
// 后序遍历
void PostOrder_Tree_Walk()
{
postOrder_Tree_Walk(root); // 传入根节点
cout << endl;
}
// 递归查找
BSTNode* Tree_Search(double key)
{
return tree_Search(root, key); // 传入根节点和待查找的关键字key
}
// 迭代查找
BSTNode* Iterative_Tree_Search(double key)
{
return iterative_Tree_Search(root, key); // 传入根节点和待查找的关键字key
}
// 最小关键字
BSTNode* Tree_Minimum(BSTNode *x)
{
return tree_Minimum(x); // 传入子树树根，查询子树的最小关键字
}
// 最大关键字
BSTNode* Tree_Maximum(BSTNode *x)
{
return tree_Maximum(x); // 传入子树树根，查询子树的最大关键字
}
// 后继
BSTNode* Tree_Successor(BSTNode *x)
{
return tree_Successor(x); // 查询节点x的后继节点
}
// 前驱
BSTNode* Tree_Predecessor(BSTNode *x)
{
return tree_Predecessor(x); // 查询节点x的前驱节点
}
// 插入
void Tree_Insert(double key)
{
BSTNode *z = new BSTNode(key, NULL, NULL, NULL); // 根据关键字生成新节点
if (z == NULL)
return;
tree_Insert(root, z); // 传入树根以及待插入的结点
}
// 删除
void Tree_Delete(double key)
{
BSTNode *z, *node;
z = iterative_Tree_Search(root, key); // 根据给定的关键字，查找树中是否存在该关键字的结点
if (z != NULL) // 若存在
{
node = tree_Delete(root, z); // 传入树根以及待删除的结点
if (node != NULL)
delete node;
}
}
// 销毁二叉搜索树
void Tree_Destory()
{
tree_Destory(root);
}
~BSTree()
{
Tree_Destory();
}
};
int main()
{
int i, j, n;
double *arr;
BSTree *tree = new BSTree();
cout << "请输入结点/关键字个数: " << endl;
cin >> n;
arr = new double[n];
cout << "请依次输入关键字(注意每棵子树的根节点都要比它的孩子结点先输入): " << endl;
for (i = 0; i < n; i++)
{
cin >> arr[i]; // 依次输入关键字
tree->Tree_Insert(arr[i]); // 调用插入函数，根据关键字生成二叉搜索树
}
cout << endl;
cout << "二叉搜索树先序遍历的结果为: ";
tree->PreOrder_Tree_Walk();
cout << "二叉搜索树中序遍历的结果为: ";
tree->InOrder_Tree_Walk();
cout << "二叉搜索树后序遍历的结果为: ";
tree->PostOrder_Tree_Walk();
cout << endl;
double seaKey;
cout << "请输入要查找的结点关键字: " << endl;
cin >> seaKey;
BSTNode *seaNode = tree->Tree_Search(seaKey);
if (seaNode)
cout << "查找成功" << endl;
else
cout << "查找失败, 关键字为" << seaKey << "的结点不存在" << endl;
cout << endl;
double delKey;
cout << "请输入要删除的结点关键字: " << endl;
cin >> delKey;
tree->Tree_Delete(delKey);
// 通过先序与中序遍历，或者中序与后序遍历可以唯一确定一棵二叉树
// 因此此处可以验证删除后的二叉搜索树是否与你预想的一样
cout << "删除操作后先序遍历二叉搜索树的结果为: ";
tree->PreOrder_Tree_Walk();
cout << "删除操作后中序遍历二叉搜索树的结果为: ";
tree->InOrder_Tree_Walk();
cout << endl;
tree->Tree_Destory(); // 销毁二叉树
delete[] arr;
system("pause");
return 0;
}附注：
1、卫星数据：
卫星数据是指一条记录中除了关键字key以外的其他数据。因为一个记录可能包含多个数据项，但是一般的排序算法只关心key，其他的项都是跟着key走，像“卫星”一样。另外，也可参考《算法导论》（中文第3版）第81页，也即书中“第二部分”的序言中所涉及到的卫星数据的相关说法。
2、θ(n)：
θ是一个渐进符号，在表示时间复杂度或空间复杂度时可能会用到。当仅表示上界时，使用符号Ω(n)；当仅表示下界时，使用符号O(n)；当表示上下界都渐进于某个函数时，使用符号θ(n)。
1697
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
