Project Euler15 给定一个20*20的方格，从左上角到右下角的路径有多少条？（只允许向右和向下走)

首先我们来讨论一下2*2方格的情况：

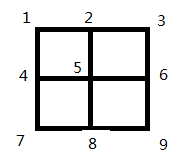
从结点1到结点9的走法：

1-2-3-6-9

1-2-5-6-9

1-2-5-8-9

1-4-7-8-9

1-4-5-6-9

1-4-5-8-9

共有6种不同的走法，仔细的读者会发现，在结点3，6，7，8到结点9的通道只有一种，是的，这将会是以后解决问题的关键之一。

现在我们将方格数推广到n，定义f（n,n）为结点（0，0）到结点（n，n）的通道数。

算法如下：

方法一：递推法

• 递推公式为f(n,n)=f(n-1,n)+f(n,n-1)；
• 初始化条件:当0 <= i <= n,f(n,i)=1,f(i,n)=1。（初始条件的寻找，还得看读者的观察能力了）

方法二：排列组合

• f(n,n)=c(n,n+n)，其中c(n,n+n)表示n+n中取n

现在我只研究方法一，实现的代码如下：

#include <iostream>
#include <TIME.H>
using namespace std;
#define MAX_X 21
#define MAX_Y 21
/