Python 动态规划解决不同路径问题

最新推荐文章于 2023-09-11 23:08:37 发布

oyall520

最新推荐文章于 2023-09-11 23:08:37 发布

阅读量2.1k

点赞数 2

分类专栏： LeetCode刷题文章标签： leetcode 动态规划

本文链接：https://blog.csdn.net/oyall520/article/details/105418833

版权

LeetCode刷题专栏收录该内容

28 篇文章 1 订阅

订阅专栏

一、【LeetCode 62】不同路径

1. 题目描述

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？
在这里插入图片描述
例如，上图是一个7 x 3 的网格。有多少可能的路径？

示例 1:

输入: m = 3, n = 2
输出: 3
解释:
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右

示例 2:

输入: m = 7, n = 3
输出: 28

提示：
1 <= m, n <= 100
题目数据保证答案小于等于 2 * 10 ^ 9

2. 解题思路

这是一个经典的动态规划问题，关键是要想明白如何去计算其中的某一个格子到达它的路径有多少条，计算方式就是到达它上面的格子的路径数加上到达它左边的格子的路径数。

首先初始化一个二维数组memo（m行n列，每个元素的初始值为0）memo = [[0 for j in range(n)] for i in range(m)]
接着对memo数组的第一行和第一列进行初始化：因为机器人每次只能向下或者向右移动一步，不能向左向上往回走，所以可以将 memo 数组的第一行和第一列的值全部初始化为1（因为到达第一行的每个格子只有一直往右走这一种走法，同理到达第一列的每个格子也只有一直往下走这一种走法）
接下来就是双重循环，考虑数组内部的值，每一个格子的值都等于上一个格子的值加上左边格子的值memo[i][j] = memo[i - 1][j] + memo[i][j - 1]，可见下图：
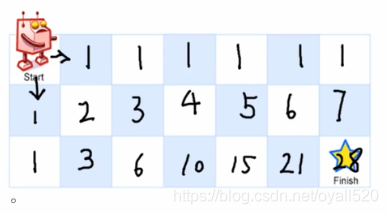
这样依次算出memo数组的每一个值后，直接返回右下角的数值即可return memo[-1][-1]。

3. 代码

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        memo = [[0 for j in range(n)] for i in range(m)]
        for i in range(m):
            memo[i][0] = 1
        for j in range(n):
            memo[0][j] = 1
        for i in range(1, m):
            for j in range(1, n):
                memo[i][j] = memo[i - 1][j] + memo[i][j - 1]
        return memo[-1][-1]

二、【LeetCode 63】不同路径II

1. 题目描述

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？
在这里插入图片描述
网格中的障碍物和空位置分别用 1 和 0 来表示。

说明： m 和 n 的值均不超过 100。

示例 1:

输入:
[
  [0,0,0],
  [0,1,0],
  [0,0,0]
]
输出: 2
解释:
3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

2. 解题思路

本题和上题不同之处在于本题设置了障碍物，机器人不再是畅通无阻的前进，思路有点点绕：

首先由障碍网格获取行数m和列数n，进行边界条件判断，当m=0或n=0，换句话说就是只有一列或一行时，有障碍物的存在永远无法到达终点，这种情况直接返回0即可。
接下来创建一个二维数组memo（m行n列，数组内所有值均为0），然后考虑特殊情况：当起始的地方就有一个障碍物（也就是obstacleGrid[0][0] == 1时），也是无法走到终点的，直接return 0；起始地没有障碍物时就可将 memo[0][0] 置为1。
接下来最关键的就是memo数组第一行和第一列的初始化：因为本题存在障碍物，所以本题不能像上题那样单纯的将第一行和第一列全部置为1，因为一旦第一行或第一列出现障碍物，后面的格子就无法到达了，应为0。所以要进行判断，可以先考察 obstacleGrid 中每一行的第一个数字for i in range(1, m)是否为1if obstacleGrid[i][0] == 1:若是的话直接跳出循环，后面的格子就不用看了，全部为最开始创建数组时设置的0；若不是，就可将memo[i][0]置为1.每一列的第一个数字同理。
再接着就是双重循环看obstacleGrid内部数字，若发现obstacleGrid[i][j] 等于 1，就将相应的 memo[i][j] 置为 0；否则还是与上题相同，当前格子的值=上一个格子的值+左边格子的值：memo[i][j] = memo[i - 1][j] + memo[i][j - 1] 见下图：

3. 代码

class Solution:
    def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
        m = len(obstacleGrid)
        n = len(obstacleGrid[0])
        if m == 0 or n == 0:
            return 0
        memo = [[0 for j in range(n)]for i in range(m)]
        if obstacleGrid[0][0] == 1:
            return 0
        memo[0][0] = 1
        for i in range(1, m):
            if obstacleGrid[i][0] == 1:
                break
            else:
                memo[i][0] = 1
        for j in range(1, n):
            if obstacleGrid[0][j] == 1:
                break
            else:
                memo[0][j] = 1
        for i in range(1, m):
            for j in range(1, n):
                if obstacleGrid[i][j] == 1:
                    memo[i][j] = 0
                else:
                    memo[i][j] = memo[i - 1][j] + memo[i][j - 1]
        return memo[-1][-1]

三、【LeetCode 64】最小路径和

1. 题目描述

给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明： 每次只能向下或者向右移动一步。

示例:

输入:
[
  [1,3,1],
  [1,5,1],
  [4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。

2. 解题思路

本题与62题类似，62题求得是从起点左上角到终点右下角的所有不同路径，而本题相当于是求这些路径中和最小的一条，思路差不多，依旧使用动态规划——

首先还是获取网格的行数m和列数n，并进行边界判断：当m=0且n=0，也就是说当这个网格为空时，没有路径可走，直接返回0即可。
接下来创建二维数组memo（m行n列，数组内所有值全为0），设置 memo[0][0] 的值：memo[0][0] = grid[0][0]（到达第一个格子的最短路径肯定是自身的值）
接下来初始化memo数组的第一行和第一列，因为机器人每次只能向下或者向右移动一步，不能向左向上往回走，所以可以将 memo 数组的第一行每个格子的值等于前一个格子的值加上当前对应的grid里的值：memo[0][j] = memo[0][j-1] + grid[0][j]，第一列同理（因为到达第一行的每个格子只有一直往右走这一种走法，同理到达第一列的每个格子也只有一直往下走这一种走法）
接下来就是双重循环，62题是将上一个格子的值加上左边格子的值就是当前格子的值，而本题是取上一个格子和左边格子中更小的那一个加上当前格子对应grid里的值，才是memo[i][j]的值：memo[i][j] = min(memo[i-1][j], memo[i][j-1]) + grid[i][j]，见下图：
像这样算出memo所有值后，返回最后一个值即可：return memo[-1][-1]

3. 代码

class Solution:
    def minPathSum(self, grid: List[List[int]]) -> int:
        m = len(grid)
        n = len(grid[0])
        if m == 0 and n == 0:
            return 0
        memo = [[0 for j in range(n)] for i in range(m)]
        memo[0][0] = grid[0][0]
        for i in range(1, m):
            memo[i][0] = memo[i-1][0] + grid[i][0]
        for j in range(1, n):
            memo[0][j] = memo[0][j-1] + grid[0][j]
        for i in range(1, m):
            for j in range(1, n):
                memo[i][j] = min(memo[i-1][j], memo[i][j-1]) + grid[i][j]
        return memo[-1][-1]

四、【LeetCode 120】三角形最小路径和

1. 题目描述

给定一个三角形，找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。

例如，给定三角形：

[
     [2],
    [3,4],
   [6,5,7],
  [4,1,8,3]
]
自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

说明：

如果你可以只使用 O(n) 的额外空间（n 为三角形的总行数）来解决这个问题，那么你的算法会很加分。

2. 解题思路

要找出自顶向下的最小路径和，并且每一步只能移动到下一行中相邻的结点上。乍一看有点像求解二叉树中的最小路径和，但是二叉树可以直接由当前节点表示出左右子节点，本题是数组，看起来似乎不太方便，其实可以用索引来表示：比如当前元素的位置为triangle[row][col]，那么它下一行相邻的两个元素分别为triangle[row+1][col] 和 triangle[row+1][col+1]

本题我们不用自顶向下的方法，而是采用自底向上求解，从倒数第二行开始计算，就拿示例来说：当遍历到6时，接下来的最小路径肯定是 6 + min(4, 1) = 6 + 1 = 7；遍历到5时，接下来的最小路径肯定是 5 + min(1, 8) = 5 + 1 = 6；遍历到7时，接下来的最小路径肯定是 7 + min(8, 3) = 7 + 3 = 10，此时的数组可等价为（最后一行不变，自底向上计算）：

[
     [2],
    [3,4],
   [7,6,10],
  [4,1,8,3]
]

同理我们可以根据倒数第二行的结果求解倒数第三行的值：当遍历到3时，接下来的最小路径肯定是 3 + min(7, 6) = 3 + 6 = 9；当遍历到4时，接下来的最小路径肯定是 4 + min(6, 10) = 4 + 6 = 10，此时的数组等价为：

[
     [2],
    [9,10],
   [7,6,10],
  [4,1,8,3]
]

最后由倒数第三行的结果求解倒数第四行的值，也就是第一行：2 + min(9, 10) = 2 + 9 = 11

[
     [11],
    [9,10],
   [7,6,10],
  [4,1,8,3]
]

由图可知最后的结果即为11，直接返回 triangle[0][0]即可。

具体实现如下：

首先判空，当二维数组 triangle 不存在时，最小路径和自然也不存在，直接返回0即可；
接下来求出该二维数组一共有多少行：n = len(triangle)；
然后从倒数第二行开始向上遍历：for row in range(n - 2, -1, -1)，并由当前行计算出当前行的列数，再进行遍历：for col in range(0, len(triangle[row]))，求出从下往上到达当前节点的最小路径和：triangle[row][col] += min(triangle[row+1][col], triangle[row+1][col+1])；
最后返回 triangle[0][0] 即可。

3. 代码

class Solution:
    def minimumTotal(self, triangle: List[List[int]]) -> int:
        if not triangle:
            return 0
        n = len(triangle)
        for row in range(n - 2, -1, -1):
            for col in range(0, len(triangle[row])):
                triangle[row][col] += min(triangle[row+1][col], triangle[row+1][col+1])
        return triangle[0][0]

oyall520

关注

2
点赞
踩
20

收藏

觉得还不错? 一键收藏
0
评论
Python 动态规划解决不同路径问题

目录一、【LeetCode 62】不同路径1. 题目描述2. 解题思路3. 代码二、【LeetCode 63】不同路径II1. 题目描述2. 解题思路3. 代码三、【LeetCode 64】最小路径和1. 题目描述2. 解题思路3. 代码一、【LeetCode 62】不同路径1. 题目描述一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为“Start” ）。机器人每次只能...
复制链接

扫一扫