链接:
基于模型的混合多目标算法的研究 - 豆丁网
http://www.docin.com/p-1088777086.html
(1) 研究背景意义

RM-MEDA(Regularity Model-Based Miulti-Objective Estimation of Distribution Algorithm)
(2)多目标中的相关概念

Pareto最优解:
在求解多目标函数最大化问题的时候:
就是在决策空间(x的取值范围)中存在A,B使得f(A)>=f(B) 并且存在等号不成立的情况(不然可能就是一个点了)则此时的A点就被成为Pareto最优解。
PS : Pareto Set 最优解定义下的x组成的集合 PF:Pareto Function PS对应的目标空间的解集
i.e: 说明决策空间-------目标空间

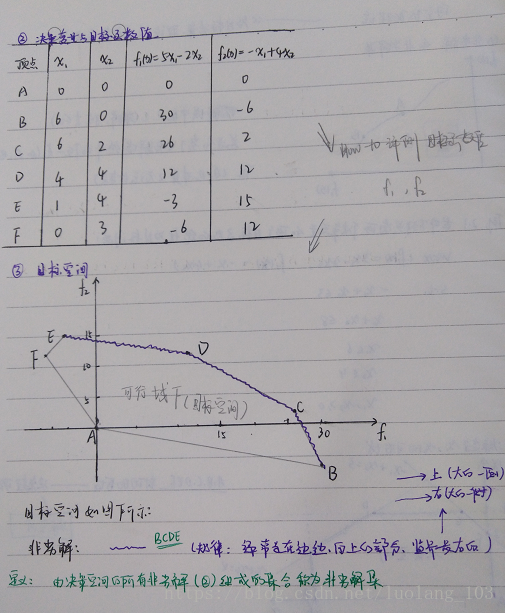
(3)个体支配i关系

自己的理解: 现实的问题中存在的那种,多个目标,多种策略方案 ,各种不同的方案,都至少在一个目标函数上达到现阶段的最优的个体,则称它为支配
(4)算法基础:









 本文介绍了基于模型的混合多目标算法RM-MEDA的基础概念及应用背景。探讨了多目标优化中的Pareto最优解和个体支配关系,并概述了该算法在解决复杂优化问题中的优势。
本文介绍了基于模型的混合多目标算法RM-MEDA的基础概念及应用背景。探讨了多目标优化中的Pareto最优解和个体支配关系,并概述了该算法在解决复杂优化问题中的优势。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








