定积分_定积分加减能拆开-CSDN博客

本文链接：https://blog.csdn.net/luols/article/details/5594025

本文介绍了一种通过将区间划分并近似为多个矩形来计算定积分的方法，并以cos(x)函数为例展示了具体的实现过程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

定积分的原始定义如下：

这个式子就是求函数f(x)在区间(a,b)的定积分，其实对于定积分来说，开、闭区间都不影响最后的积分值，也就是说，无论区间是(a,b)、[a,b)、(a,b]还是[a,b]，最后的积分值都是一样的，因为从几何意义上讲，定积分就是求面积，而一条直线或线段是没有任何面积可言的。

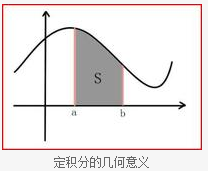
定积分几何意义
我们回想一下定积分的原始定义，是先把区间切分成“无数”块，把每一小块近似看成一个小矩形，把每个小矩形的面积迭加起来就是最终所要的结果。所以区间分得越多，结果就越精确，但考虑到效率问题，在程序中并不是越细越好，只要结果在我们的误差范围之内就可以了。

下面就以f(x) = cos(x)为例，求其在(a,b)区间的定积分（面积），核心代码如下：

/// <summary> /// 定积分核心算法 /// </summary> /// <param name="a">区间的起点</param> /// <param name="b">区间的终点</param> /// <param name="step">把区间切分成step块</param> /// <returns>积分值（面积）</returns> private double Jifen(double a, double b, int step) { double Area = 0.0; double valueOfY; //记录每一块小矩形的高，即函数值 double dx = (b - a) / (double)step; //把区间切成step块后就可得每块小矩形的宽 for (int i = 0; i < step; i++) { valueOfY = Math.Cos(a + (i + 1) * dx); //获取每块小矩形的高 Area += dx * valueOfY; //迭加每块小矩形的面积 } return Area; //返回最终结果，此时就是定积分近似值（也只能是近似值:) ） }