无约束优化算法之拟牛顿法

拟牛顿法

牛顿法在理论上有很好的效果，然而对于大规模问题，函数的海塞矩阵计算待解特别大或者难以得到，即便得到海塞矩阵我们还需要求解一个大规模线性方程组。那么能否使用海塞矩阵或其逆矩阵的近似来进行牛顿迭代呢？拟牛顿法便是这样的算法，它能够在每一步以较小的代价生成近似矩阵，并且使用近似矩阵代替海塞矩阵，而产生的迭代序列仍具有超线性收敛的性质。
拟牛顿法不计算海塞矩阵${\nabla }^{2}f(x)$，而是构造其近似矩阵$B^k$或其逆的近似矩阵$H^k$。我们希望$B^k$或$H^k$仍然保留海塞矩阵的部分性质，例如使得$d^k$仍然为下降方向。

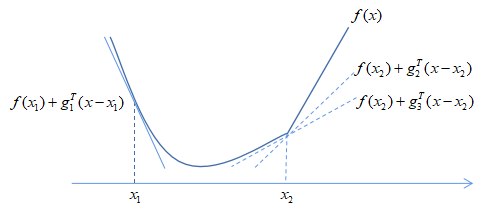
一、割线方程
回顾牛顿法的推导过程。设$f(x)$是二阶连续可微函数，根据泰勒展开，向量值函数$\nabla f(x)$在点$x^{k+1}$处的近似为：
$$\nabla f(x)=\nabla f(x^{k+1})+{\nabla }^{2}f(x^{k+1})(x-x^{k+1})+O(||x-x^{k+1}||)\text{\hspace{1em}(1)}$$
令$x=x^k,s^k=x^{k+1}-x^k$及$y^k=\nabla f(x^{k+1})-\nabla f(x^k)$，得到
$${\nabla }^{2}f(x^{k+1})s^k+O(||s^k||)=y^k\text{\hspace{1em}(2)}$$
忽略高阶项$||s^k||$，我们希望海塞矩阵的近似矩阵$B^{k+1}$满足方程
$$y^k=B^{k+1}{s}^k\text{\hspace{1em}(3)}$$
或者其逆矩阵的近似矩阵$H^{k+1}$满足方程
$$s^k=H^{k+1}{y}^k\text{\hspace{1em}(4)}$$
并称（3）式与（4）式为割线方程。
在通常情况下，近似矩阵$B^{k+1}$或$H^{k+1}$是由上一步迭代加上一个修正得到的，并且要求满足割线方程。这里先给出拟牛顿法的一般计算框架

---

拟牛顿算法的一般算法框架

1. 给定$x^0\in \mathbb{R}$，初始矩阵$B^0\in {\mathbb{R}}^{n\times n}$或$H^0$，令$k=0$
2. while 未达到停机准则 do
3. 计算方向$d^k=-(B^k{)}^{-1}\nabla f(x^k)$或$d^k=-H^k\nabla f(x^k)$
4. 通过线搜索找到合适的步长${\alpha }_k>0$，令$x^{k+1}=x^k+{\alpha }^k{d}^k$
5. 更新海塞矩阵的近似矩阵$B^{k+1}$或其逆矩阵的近似矩阵$H^{k+1}$
6. $k\leftarrow k+1$
7. end while

---

二、BFGS算法
在实际应用中基于$H^k$的拟牛顿法更加实用，这是因为根据$H^k$计算下降方向$d^k$不需要求解线性方程组，而求解线性方程组在大规模问题上是非常耗时的。

后续我们重点关注在以$H^k$为目标的拟牛顿计算方法
这里给出秩2的BFGS公式推导过程，我们采用待定系数法推导公式，设
$$B^{k+1}=B^k+au{u}^T+bv{v}^T$$
其中$u,v\in {\mathbb{R}}^n,a,b\in \mathbb{R}$。根据割线方程（3）有
$$B^{k+1}{s}^k=(B^k+au{u}^T+bv{v}^T)s^k=y^k$$
整理可得
$$(a\cdot u^T{s}^k)u+(b\cdot v^T{s}^k)v=y^k-B^k{s}^k$$
我们通过选取$u$和$v$让以上等式成立即可。实际上$u$和$v$有非常多的取法，一种最直接的取法是让上面灯饰左右两边分别对应相等，即
$$\begin{array}{r}u=y^k,a\cdot u^T{s}^k=1,\\ v=B^k{s}^k,b\cdot v^T{s}^k=-1\end{array}$$
因此得到更新方式
$$B^{k+1}=B^k+\frac{y^k(y^k{)}^T}{(s^k{)}^T{y}^k}-\frac{B^k{s}^k(B^k{s}^k{)}^T}{(s^k{)}^T{B}^k{s}^k}\text{\hspace{1em}(5)}$$
（5）式被成为基于$B^k$的BFGS公式，同理假设$H^k=(B^k{)}^{-1}$，可推出基于$H^k$的BFGS公式
$$H^{k+1}=(I-{\rho }_k{s}^k(y^k){)}^T{H}^k(I-{\rho }_k{s}^k(y^k))+{\rho }_k{s}^k(s^k{)}^T\text{\hspace{1em}(6)}$$
其中${\rho }_k=\frac{1}{(s^k{)}^T{y}^k}$。容易看出，若要BFGS公式更新产生的矩阵$H^{k+1}$正定，一个充分条件式不等式$(s^k{)}^T{y}^k>0$成立且上一步更新矩阵$H^k$正定，在问题求解过程中，不等式不一定会得到满足，此时应该使用Wolfe准则的线搜索来迫使不等式成立。
BFGS公式式目前最有效的拟牛顿更新格式之一，它有比较好的理论性质，实现起来也并不复杂，通过对（6）式进行改动可得到优先内存的BFGS格式（L-BFGS），它是常用的处理大规模优化问题的拟牛顿算法。

BFGS算法实现与数值实验

BFGS代码实现

function [fmin, xmin] = BFGS(func, gfunc, x0, epsilon)

HOld = eye(length(x0));

maxIter = 500;
xOld = x0;
iIter = 1;


while iIter < maxIter
    gOld = feval(gfunc, xOld);
    dk = -HOld * gOld;
    [~, ~, alpha] = armijo_rule(func, gfunc, xOld, 0.2, dk);
    xNew = xOld + alpha * dk;
    gNew = feval(gfunc, xNew);
    
    if norm(gNew, 2) < epsilon
        xmin = xNew;
        break;
    end
    
    gDiff = gNew - gOld;
    xDiff = xNew - xOld;
    I = eye(length(xNew));
    rho = 1 / ((xDiff)' * gDiff);
    HNew = (I - rho * gDiff * xDiff')' * HOld * (I - rho * gDiff * xDiff') ...
        + rho * xDiff * xDiff';
    HOld = HNew;
    xOld = xNew;
    iIter = iIter + 1;
end


if iIter == maxIter
    fprintf('exceed maximum iteration, and not found xmin\n');
    xmin = xNew;
end

fmin = feval(func, xmin);


end

armijo-rule代码实现

function [fnew, xnew, alpha] = armijo_rule(func, gfunc, x0, alpha0, dk)

c1 = 1e-3;
alpha = alpha0;
gamma = 0.8;

iIter = 0;
iterMax = 200;
alphaMin = 1e-5;

while iIter < iterMax 
    
    xnew = x0 + alpha * dk;
    fnew = feval(func, xnew);
    f0 = feval(func, x0);
    if fnew <= f0 + c1 * feval(gfunc, x0)' * dk
        break;
    end
    
    if alpha < alphaMin
        break;
    end
    
    alpha = gamma * alpha;
    iIter = iIter + 1;   
end

if iIter == iterMax
    alpha = alphaMin;
    fprintf('reach maximum iteration, and not found suitable alpha.\n');
end

xnew = x0 + alpha * dk;
fnew = feval(func, xnew);

end

算例
(0) $f_0=x_1^2+2x_2^2-2x_1{x}_2-4x_1$
(1) $f_1=x_2^2+x_2^2-x_1{x}_2-10x_1-4x_2$
(2) $f_2=x_1^2-2x_1{x}_2+2x_2^2-4x_1$
(3) $f_3=x_1^2-2x_1{x}_2+3x_2^2-4x_1-5x_2$

数值实验代码

% test bfgs

% example 
x0 = [1, 1]';
epsilon = 1e-6;

[fmin, xmin] = BFGS('bfgsTestFun0', 'bfgsTestGfun0', x0, epsilon);
fprintf('fmin = %f, xmin = (%f, %f)\n', fmin, xmin(1), xmin(2));
[x, f] = fminsearch('bfgsTestFun0', x0);
fprintf('build-in search: fmin = %f, xmin = (%f, %f)\n', f, x(1), x(2));

% exercise
% ex 4-4 (1)
x0 = [1, 1]';
epsilon = 1e-6;

[fmin, xmin] = BFGS('bfgsTestFun1', 'bfgsTestGfun1', x0, epsilon);
fprintf('fmin = %f, xmin = (%f, %f)\n', fmin, xmin(1), xmin(2));
[x, f] = fminsearch('bfgsTestFun1', x0);
fprintf('build-in search: fmin = %f, xmin = (%f, %f)\n', f, x(1), x(2));

% ex 4-4 (2)
x0 = [1, 1]';
epsilon = 1e-6;

[fmin, xmin] = BFGS('bfgsTestFun2', 'bfgsTestGfun2', x0, epsilon);
fprintf('fmin = %f, xmin = (%f, %f)\n', fmin, xmin(1), xmin(2));
[x, f] = fminsearch('bfgsTestFun2', x0);
fprintf('build-in search: fmin = %f, xmin = (%f, %f)\n', f, x(1), x(2));

% ex 4-4 (3)
x0 = [1, 1]';
epsilon = 1e-6;

[fmin, xmin] = BFGS('bfgsTestFun3', 'bfgsTestGfun3', x0, epsilon);
fprintf('fmin = %f, xmin = (%f, %f)\n', fmin, xmin(1), xmin(2));
[x, f] = fminsearch('bfgsTestFun3', x0);
fprintf('build-in search: fmin = %f, xmin = (%f, %f)\n', f, x(1), x(2));

function f = bfgsTestFun0(x)

f = x(1)^2 + 2 * x(2)^2 - 2 * x(1) * x(2) - 4 * x(1);

end

function f = bfgsTestFun1(x)

f = x(1)^2 + x(2)^2 - x(1) * x(2) - 10 * x(1) - 4 * x(2);

end

function f = bfgsTestFun2(x)

f = x(1)^2 - 2 * x(1) * x(2) + 2 * x(2)^2 - 4 * x(1);

end

function f = bfgsTestFun3(x)

f = x(1)^2 - 2 * x(1) * x(2) + 3 * x(2)^2 - 4 * x(1) - 5 * x(2);

end

function g = bfgsTestGfun0(x)

g = [2 * x(1) - 2 * x(2) - 4; ...
    -2 * x(1) + 4 * x(2)];

end

function g = bfgsTestGfun1(x)

g = [2 * x(1) - x(2) - 10;...
     2 * x(2) - x(1) - 4];

end

function g = bfgsTestGfun2(x)

g = [2 * x(1) - 2 * x(2) - 4;...
     -2 * x(1) + 4 * x(2)];

end

function g = bfgsTestGfun3(x)

g = [2 * x(1) - 2 * x(2) - 4;...
    -2 * x(1) + 6 * x(2) - 5];

end

计算结果为：

>> bfgsTest
fmin = -8.000000, xmin = (3.999999, 1.999999)
build-in search: fmin = -8.000000, xmin = (3.999976, 1.999973)
fmin = -52.000000, xmin = (7.999999, 6.000000)
build-in search: fmin = -52.000000, xmin = (8.000014, 5.999992)
fmin = -8.000000, xmin = (3.999999, 1.999999)
build-in search: fmin = -8.000000, xmin = (3.999976, 1.999973)
fmin = -14.125000, xmin = (4.250000, 2.250000)
build-in search: fmin = -14.125000, xmin = (4.249959, 2.249993)

三、L-BFGS算法
拟牛顿法虽然克服了计算海塞矩阵的困难，但是它仍然无法应用在大规模优化问题上。一般来说，拟牛顿矩阵$B^k$或$H^k$是稠密矩阵，而存储稠密矩阵要小号$O(n^2)$的内存，这对于大规模问题，尤其是处理高分辨率图像问题时是不可能接受的。本部分介绍有效内存的BFGS方法解决了这一问题，从而使得人们在大规模问题上也可应用拟牛顿方法加速迭代的收敛。
L-BFGS方法根据公式（5）和（6）变形而来的。为了推导方便，我们以$H^k$的更新公式（6）为基础推导相应的L-BFGS，为了方便推导，引入新的记号重写公式（6）
$$H^{k+1}=(V^k{)}^T{H}^k{V}^k+\rho s^k(s^k{)}^T\text{\hspace{1em}(7)}$$
其中
$${\rho }^k=\frac{1}{(y^k{)}^T{s}^k},V^k=I-{\rho }^k{y}^k(s^k{)}^T\text{\hspace{1em}(8)}$$
观察到（7）式有类似地推的性质，为了我们将（7）式递归地展开$m$次，其中$m$是一个给定的整数：
$$\begin{array}{rl}& H^k=\\ & (V^{k-m}\cdots V^{k-1}{)}^T{H}^{k-m}(V^{k-m}\cdots V^{k-1})+\\ & {\rho }_{k-m}(V^{k-m+1}\cdots V^{k-1}{)}^T{s}^{k-m}(s^{k-m}{)}^{（}{V}^{k-m+1}\cdots V^{k-1}）+\\ & {\rho }_{k-m+1}(V^{k-m+2}\cdots V^{k-1}{)}^T{s}^{k-m+1}(s^{k-m+1}{)}^{（}{V}^{k-m+2}\cdots V^{k-1}）+\cdots +\\ & {\rho }_{k-1}{s}^{k-1}(s^{k-1}{)}^T\end{array}\text{\hspace{1em}(9)}$$
为了达到节省内存的目的，（7）式不能无限展开下去，当这会产生一个问题，$H^{k-m}$还是无法求出。一个自然的想法就是用$H^{k-m}$的近似矩阵来代替$H^{k-m}$进行计算，近似矩阵的选取方式很多，但基本原则是要保证近似矩阵具有非常简单的结构，假定我们给出了$H^{k-m}$的一个近似矩阵（9）式便可以用于计算拟牛顿迭代。
在拟牛顿迭代中，实际上并不需要计算$H^k$的显示形式，只需要利用$H^k\nabla f(x^k)$来计算迭代方向$d^k$。为此先直接给出一个利用展开式（9）直接求解$H^k\nabla f(x^k)$的算法。见L-BFGS双循环递归算法。改算法的设计很精妙，充分利用了（9）式的结构来尽量节省计算$H^k\nabla f(x^k)$的开销。

---

L-BFGS双循环递归算法

1. 初始化$q\leftarrow \nabla f(x^k)$
2. for i = k-1,k-2, …, k-m do
3. 计算并保存${\alpha }_i\leftarrow {\rho }_i(s^i{)}^{T}q$.
4. 更新$q\leftarrow q-{\alpha }_i{y}^i$.
5. end for
6. 初始化$r\leftarrow {\hat{H}}^{k-m}q$，其中${\hat{H}}^{k-m}$是$H^{k-m}$的近似矩阵
7. for i = k-m, k-m+1, …, k-1 do
8. 计算$\beta \leftarrow {\rho }_i(y^i{)}^{T}r$
9. 更新$r\leftarrow r+({\alpha }_i-\beta )s^i$
10. end for
11. 输出$r$，即$H^k\nabla f(x^k)$

---

上述L-BFGS双循环递归算法约需要4mn次乘法运算与2mn次加法运算，若近似矩阵${\hat{H}}^{k-m}$是对角矩阵，则额外需要n次乘法运算。由于m不会很大，因此该算法的复杂度为$O(mn)$。算法所需要的额外存储为临时变量${\alpha }_i$，它的大小是$O(m)$。综上所述，L-BFGS双循环算法是非常高效的。
近似矩阵${\hat{H}}^{k-m}$的取法可以是对角矩阵${\hat{H}}^{k-m}={\gamma }_{k}I$，其中
$${\gamma }_k=\frac{(s^{k-1}{)}^T{y}^{k-1}}{(y^{k-1}{)}^T{y}^{k-1}}$$
这恰好是BB方法的第一个步长。

这里给出L-BFGS的具体算法流程

---

1. 选择初始点$x^0$，参数$m>0,k\leftarrow 0$.
2. while 未达到收敛准者 do
3. 选择近似矩阵${\hat{H}}^{k-m}$.
4. 使用双循环算法计算下降方向$d^k=-H^k\nabla f(x^k)$
5. 使用线搜索算法计算满足Wolfe准则的步长${\alpha }_k$.
6. 更新$x^{k+1}=x^k+{\alpha }_k{d}^k$.
7. if k > m then
8. 从内存空间中删除$s^{k-m},y^{k-m}$.
9. end if
10. 计算并保存$s^k=x^{k+1}-x^k,y^k=\nabla f(x^{k+1})-\nabla f(x^k)$
11. $k=\leftarrow k+1$
12. end while

---

正因为L-BFGS方法的出现，人们可以使用拟牛顿类算法求解优化问题。虽然有关L-BFGS方法的收敛性依然有限，但实际应用中L-BFGS方法很快成为应用最广泛的拟牛顿类算法。