LeetCode 题解之 240. Search a 2D Matrix II

最新推荐文章于 2022-11-16 19:19:52 发布

liweiwei1419

最新推荐文章于 2022-11-16 19:19:52 发布

阅读量385

点赞数

分类专栏：算法数据结构文章标签： leetcode

本文链接：https://blog.csdn.net/lw_power/article/details/81096104

版权

算法同时被 2 个专栏收录

80 篇文章 2 订阅

订阅专栏

数据结构

62 篇文章 0 订阅

订阅专栏

240. Search a 2D Matrix II

题目描述和难度

题目描述：

编写一个高效的算法来搜索 m x n 矩阵中的一个目标值 target。该矩阵具有以下特性：

每行的元素从左到右升序排列。
每列的元素从上到下升序排列。

例如，

给定以下矩阵 matrix ：

[
  [1,   4,  7, 11, 15],
  [2,   5,  8, 12, 19],
  [3,   6,  9, 16, 22],
  [10, 13, 14, 17, 24],
  [18, 21, 23, 26, 30]
]

示例 1:

输入: matrix, target = 5
输出: true

示例 2:

输入: matrix, target = 20
输出: false

题目难度：中等。
英文网址：240. Search a 2D Matrix II 。
中文网址：240. 搜索二维矩阵 II 。

思路分析

求解关键：正确的搜索起点是从左下角或者右上角开始搜索，这是因为：
+ 从下到上，数字越来越小；
+ 从左到右，数字越来越大。
注意指针没有必要回退，这一点，在下面的代码注释中做了强调。

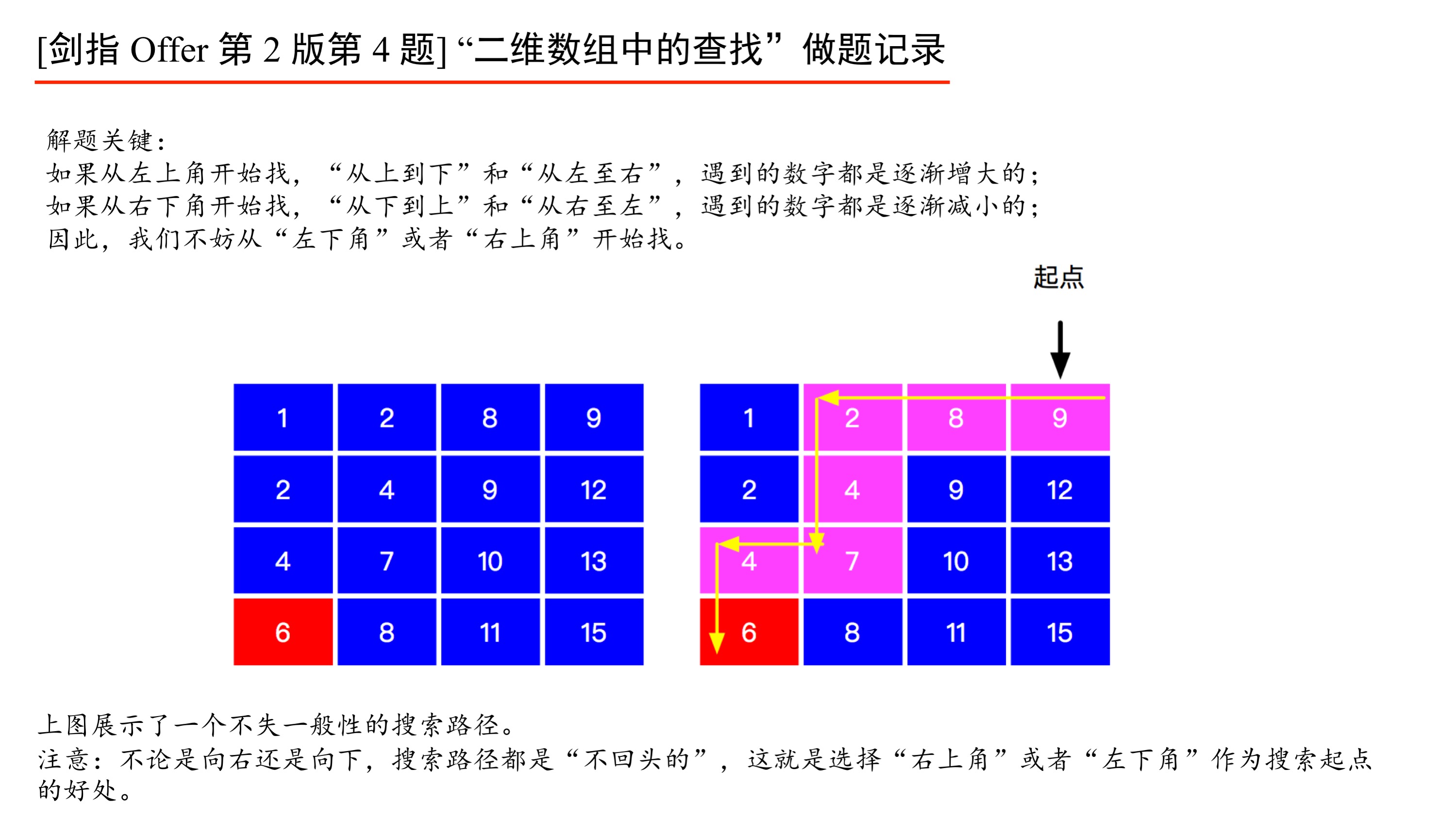
上面的图示是我最开始的想法，下面给出的参考解答 1 至参考解答 4 都是这样的，只是写法不同而已。

参考解答 5 和参考解答 6 给出了一种更简单的写法：

参考解答

参考解答1

public class Solution {

    // 从左下角开始，尝试不断向右边走
    // 右边走不动了，就向下面走，直到出边界

    public boolean searchMatrix(int[][] matrix, int target) {
        int row = matrix.length;
        if (row == 0) {
            return false;
        }
        int col = matrix[0].length;
        // 从左下角开始搜索
        int x = row - 1;
        int y = 0;
        // 每次考虑向上走
        while (x >= 0) {
            // 向上走之前，尽量向右边走
            while (y < col && matrix[x][y] < target) {
                y++;
            }
            if (y < col && matrix[x][y] == target) {
                return true;
            }
            x--;
        }
        return false;
    }
}

参考解答2：和参考解答1 是一样的，只不过写法不同。

public class Solution2 {

    public boolean searchMatrix(int[][] matrix, int target) {
        int row = matrix.length;
        if (row == 0) {
            return false;
        }
        int col = matrix[0].length;
        // 从左下角开始搜索
        int x = row - 1;
        int y = 0;
        // 每次考虑向右边走
        while (y < col) {
            // 向右边走之前，尽量向上走
            while (x >= 0 && matrix[x][y] > target) {
                x--;
            }
            // 走不动了，再向右边走
            if (x >= 0 && matrix[x][y] == target) {
                return true;
            }
            y++;
        }
        return false;
    }
}

参考解答3：和参考解答1 是一样的，只不过写法不同。

public class Solution3 {

    public boolean searchMatrix(int[][] matrix, int target) {
        int row = matrix.length;
        if (row == 0) {
            return false;
        }
        int col = matrix[0].length;
        // 从右上角开始搜索
        int x = 0;
        int y = col - 1;
        // 每次考虑向下走
        while (x < row) {
            // 向下走之前，尽量向左边走
            while (y >= 0 && matrix[x][y] > target) {
                y--;
            }
            if (y >= 0 && matrix[x][y] == target) {
                return true;
            }
            x++;
        }
        return false;
    }
}

参考解答4：和参考解答1 是一样的，只不过写法不同。

public class Solution4 {

    public boolean searchMatrix(int[][] matrix, int target) {
        int row = matrix.length;
        if (row == 0) {
            return false;
        }
        int col = matrix[0].length;
        // 从右上角开始搜索
        int x = 0;
        int y = col - 1;
        // 每次考虑向左边走
        while (y >= 0) {
            // 向左边走之前，尽量向下走
            while (x < row && matrix[x][y] < target) {
                x++;
            }
            if (x < row && matrix[x][y] == target) {
                return true;
            }
            y--;
        }
        return false;
    }
}

参考解答5：

public class Solution5 {

    // 这种写法最清晰了
    // 从右上角开始, 比较 target 和 matrix[x][y] 的值
    // 如果小于 target，则该行不可能有此数，所以 x++
    // 如果大于 target，则该列不可能有此数，所以 y--
    // 遇到边界则表明该矩阵不含 target

    public boolean searchMatrix(int[][] matrix, int target) {
        int row = matrix.length;
        if (row == 0) {
            return false;
        }
        int col = matrix[0].length;
        // 站在右上角
        int x = 0;
        int y = col - 1;
        while (x < row && y >= 0) {
            // 打开注释，可以用于调试的代码
            // System.out.println("沿途走过的数字：" + matrix[x][y]);
            if (matrix[x][y] == target) {
                return true;
            } else if (matrix[x][y] > target) {
                y--;
            } else {
                x++;
            }
        }
        return false;
    }

    public static void main(String[] args) {
        int[][] matrix = {
                {1, 4, 7, 11, 15},
                {2, 5, 8, 12, 19},
                {3, 6, 9, 16, 22},
                {10, 13, 14, 17, 24},
                {18, 21, 23, 26, 30}
        };
        int target = 5;
        Solution5 solution5 = new Solution5();
        boolean searchMatrix = solution5.searchMatrix(matrix, target);
        System.out.println(searchMatrix);
    }
}

参考解答6：和参考解答5 是一样的，只不过写法不同。

public class Solution6 {

    public boolean searchMatrix(int[][] matrix, int target) {
        int row = matrix.length;
        if (row == 0) {
            return false;
        }
        int col = matrix[0].length;

        // 站在左下角
        int x = row - 1;
        int y = 0;
        while (x >= 0 && y < col) {
            // 打开注释，可以用于调试的代码
            // System.out.println("沿途走过的数字：" + matrix[x][y]);
            if (matrix[x][y] == target) {
                return true;
            } else if (matrix[x][y] > target) {
                x--;
            } else {
                y++;
            }
        }
        return false;
    }

    public static void main(String[] args) {
        int[][] matrix = {
                {1, 4, 7, 11, 15},
                {2, 5, 8, 12, 19},
                {3, 6, 9, 16, 22},
                {10, 13, 14, 17, 24},
                {18, 21, 23, 26, 30}
        };
        int target = 5;
        Solution6 solution6 = new Solution6();
        boolean searchMatrix = solution6.searchMatrix(matrix, target);
        System.out.println(searchMatrix);
    }
}

参考解答7：二分法。

public class Solution7 {

    public boolean searchMatrix(int[][] matrix, int target) {
        int row = matrix.length;
        if (row == 0) {
            return false;
        }
        int col = matrix[0].length;
        // 站在左下角
        int x = row - 1;
        int y = 0;
        while (x >= 0 && y < col) {
            if (matrix[x][y] == target) {
                return true;
            } else if (matrix[x][y] > target) {
                // 向上走（列固定，行变化），等于最好，否则走到第 1 个小于的地方
                // 二分法定位行号
                // x--;
                if (matrix[0][y] > target) {
                    return false;
                }
                int left = 0;
                int right = x;
                while (left <= right) {
                    int mid = left + (right - left) / 2;
                    if (matrix[mid][y] == target) {
                        return true;
                    } else if (matrix[mid][y] < target) {
                        left = mid + 1;
                    } else {
                        right = mid - 1;
                    }
                }
                x = right;
            } else {
                // 二分法定位列号
                // 向右边走
                // y++;
                if (matrix[x][col - 1] < target) {
                    return false;
                }

                int left = y;
                int right = col - 1;

                while (left <= right) {
                    int mid = left + (right - left) / 2;
                    if (matrix[x][mid] == target) {
                        return true;
                    } else if (matrix[x][mid] < target) {
                        left = mid + 1;
                    } else {
                        right = mid - 1;
                    }
                }
                y = left;
            }
        }
        return false;
    }

    public static void main(String[] args) {
        int[][] matrix = {
                {1, 4, 7, 11, 15},
                {2, 5, 8, 12, 19},
                {3, 6, 9, 16, 22},
                {10, 13, 14, 17, 24},
                {18, 21, 23, 26, 30}
        };
        int target = 40;
        Solution7 solution7 = new Solution7();
        boolean searchMatrix = solution7.searchMatrix(matrix, target);
        System.out.println(searchMatrix);
    }
}