Machine Learning Exercise4

最新推荐文章于 2021-04-02 23:37:49 发布

lxk9409

最新推荐文章于 2021-04-02 23:37:49 发布

阅读量288

点赞数

CC 4.0 BY-SA版权

分类专栏： Machine Learning

本文链接：https://blog.csdn.net/lxk9409/article/details/80602250

Machine Learning 专栏收录该内容

4 篇文章

订阅专栏

本文介绍了一种使用神经网络进行手写数字识别的方法，包括数据加载与可视化、前馈计算、正则化处理、梯度计算等关键步骤。

这一次的编程练习是实现神经网络的反向传播算法，并对手写数字数据集进行分类。

Part1: Loading and Visualizing Data

% Load Training Data
fprintf('Loading and Visualizing Data ...\n')

load('ex4data1.mat');
m = size(X, 1);

% Randomly select 100 data points to display
sel = randperm(size(X, 1));
sel = sel(1:100);
displayData(X(sel, :));

randperm(n):返回一个由从1到n的数随机排列组成的数字序列。

Part 2: Loading Parameters

...

Part 3: Compute Cost (Feedforward)

（lambda=0，即忽略正则化）

网络结构：

400_25_10
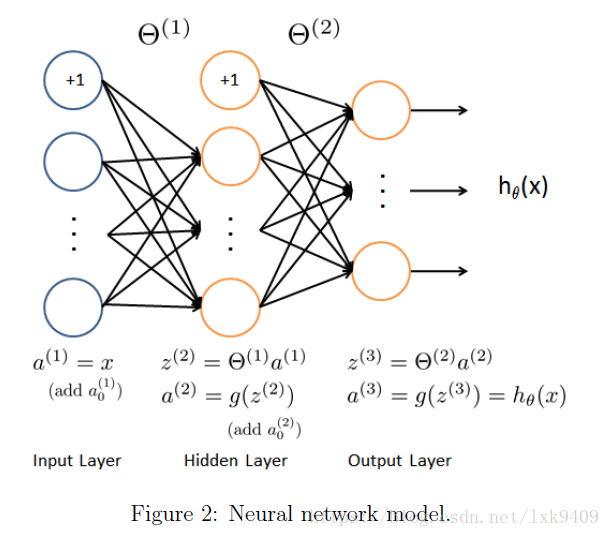
这里写图片描述

J = nnCostFunction(nn_params, input_layer_size, hidden_layer_size, ...
                   num_labels, X, y, lambda);

function [J grad] = nnCostFunction(nn_params, ...
                                   input_layer_size, ...
                                   hidden_layer_size, ...
                                   num_labels, ...
                                   X, y, lambda)

% Reshape nn_params back into the parameters Theta1 and Theta2                                   

Theta1 = reshape(nn_params(1:hidden_layer_size * (input_layer_size + 1)), ...
                 hidden_layer_size, (input_layer_size + 1));

Theta2 = reshape(nn_params((1 + (hidden_layer_size * (input_layer_size + 1))):end), ...
                 num_labels, (hidden_layer_size + 1));

J = 0;
%compute J
%Theta1 size: 25 * 401
%Theta2 size: 10 * 26
%y size: 5000 * 1
a1 = [ones(m,1),X];%5000*401
z2 = a1*Theta1';%5000*25
a2 = [ones(m,1),sigmoid(z2)];%5000*26
a3 = sigmoid(a2*Theta2');%5000*10

%变为one-hot编码
e=eye(num_labels); 
y = e(:,y)';%5000*10

J = (1/m)*sum(sum((-y.*log(a3))-((1-y).*log(1-a3))))

把y从5000*1转为5000*10的编码借助了单位矩阵
.*和.的区别：.*将元素按位置对应相乘，*遵循矩阵乘法规则

Part 4: Implement Regularization

J = (1/m)*sum(sum((-y.*log(a3))-((1-y).*log(1-a3))))+...
    (lambda/(2*m))*(sum(sum(Theta1(:,2:end).^2))+sum(sum(Theta2(:,2:end).^2)));

Part 5: Sigmoid Gradient

sigmoid函数：
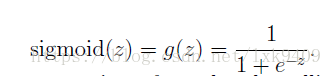
这里写图片描述
它的导函数形式如下：

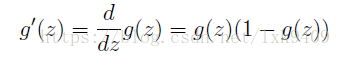
function g = sigmoidGradient(z)
g = zeros(size(z));
g = (sigmoid(z).*(1-sigmoid(z)));
end

Part 6: Initializing Pameters

为了打破对称性，网络的参数要随机初始化！在这里用的方法是选择一个ε，使得Θ取值∈[-ε，ε]

function W = randInitializeWeights(L_in, L_out)
W = zeros(L_out, 1 + L_in);
epsilon_init = 0.12;
W = rand(L_out,1 + L_in) * 2 * epsilon_init - epsilon_init;

Part 7: Implement Backpropagation

Delta1 = zeros(size(Theta1)); %25x401  
Delta2 = zeros(size(Theta2)); %10x26  

delta3 = a3 - y;    %5000*10
delta2=(delta3*Theta2(:,2:end)).*(sigmoidGradient(z2));     %5000*25

Theta1(:,1) = 0;
Theta2(:,1) = 0;
Delta1 = delta2'*a1;
Delta2 = delta3'*a2;
Theta1_grad = Delta1/m + lambda/m*Theta1;
Theta2_grad = Delta2/m + lambda/m*Theta2;